
Вэриан
.pdf4.В тексте мы предположили, что покупатели кондоминиумов принадлежат к числу жителей внутреннего кольца — т.е., лиц, которые уже снимают квартиры. Что произошло бы с ценой квартир внутреннего кольца, если бы все покупатели кондоминиумов были жителями внешнего кольца — людьми, которые в настоящий момент не снимают квартиры во внутреннем кольце?
5.Теперь предположим, что все покупатели кондоминиумов — люди из внутреннего кольца, но что каждый кондоминиум был построен из двух квартир. Что произошло бы в этом случае с ценой квартир?
6.Как вы думаете, каковы были бы последствия введения налога на число квартир, которые будут построены в длительном периоде?
7.Допустим, что кривая спроса имеет вид D(p)=100 – 2p=40. Какую цену установил бы монополист, если бы у него имелось 60 квартир для сдачи? Сколько квартир он бы сдал? Какую цену он бы установил, если бы имел 40 квартир? Сколько квартир он бы сдал?
8.Если бы рассматриваемая нами модель контроля за арендной платой допускала неограниченную передачу в субаренду, то кто в итоге получил бы квартиры во внутреннем кольце? Был бы такой исход эффективным по Парето или нет?
35

ГЛАВА 2
БЮДЖЕТНОЕ
ОГРАНИЧЕНИЕ
Экономическая теория поведения потребителя очень проста: экономисты полагают, что потребители выбирают лучший товарный набор, который могут себе позволить. Чтобы наполнить эту теорию конкретным содержанием, мы должны более точно описать, что именно подразумевается под "лучшим" и что именно подразумевается под "могут себе позволить". В настоящей главе сосредоточимся на изучении описания того, что потребитель может себе позволить, а в следующей главе — на концепции определения потребителем того, что является "лучшим". После этого мы сможем приступить к детальному изучению значения этой простой модели поведения потребителя.
2.1. Бюджетное ограничение
Начнем с рассмотрения понятия бюджетного ограничения. Предположим, что имеется некое множество товаров, в пределах которого потребитель может осуществлять свой выбор. В реальной жизни существует много товаров, выступающих объектами потребления, однако для наших целей удобно рассмотреть случай всего двух товаров, поскольку тогда можно описать поведение потребителя в отношении выбора товаров графически.
36 |
Глава 2 |
Обозначим потребительский набор данного потребителя через (х1, х2). Это просто два числа, говорящие нам о том, сколько товара 1, х1, и сколько товара 2, х2, хочет потребить данный потребитель. Иногда удобно обозначать потребительский набор лишь одним символом, скажем, X, где X — просто сокращенное обозначение указанного перечня двух чисел (х1, х2).
Предположим, что из наблюдений нам известны цены этих двух товаров, (р1, р2), и та сумма денег, которую может израсходовать потребитель, m. Тогда бюджетное ограничение потребителя может быть записано в виде
р1х1 + р2х2 m. |
(2.1) |
Здесь р1х1 — сумма денег, расходуемая потребителем на товар 1, а р2х2 — сумма денег, расходуемая им на товар 2. Бюджетное ограничение потребителя требует, чтобы сумма денег, затраченная на оба товара, не превышала общей суммы денег, которую может израсходовать данный потребитель. Доступными для потребителя наборами являются те, которые стоят не дороже m. Мы называем это множество доступных потребительских наборов при ценах (р1, р2) и доходе m бюджетным множеством данного потребителя.
2.2. Двух товаров зачастую вполне достаточно
Предпосылка о наличии всего лишь двух товаров носит более общий характер, чем можно было бы поначалу подумать, поскольку часто можно считать один из товаров представляющим все другие товары, которые потребитель мог бы захотеть потребить.
Например, если мы хотим изучить спрос потребителя на молоко, мы можем обозначить через х1 его ежемесячное потребление молока в квартах, а через х2
— все остальные товары, которые мог бы захотеть потребить данный потребитель.
Приняв эту трактовку товара 2, удобно думать о нем как о том количестве долларов, которое потребитель может истратить на все другие товары. При подобном истолковании цена товара 2 автоматически оказывается равной 1, поскольку цена одного доллара есть доллар. Таким образом, бюджетное ограничение примет вид
р1х1 + х2 m. |
(2.2) |
Данное выражение говорит нам просто о том, что сумма денег р1х1, израсходованная на товар 1, и сумма денег, израсходованная на все другие товары, х2, взятые вместе, не должны превышать общей суммы денег m, которую может расходовать данный потребитель.
БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ |
37 |
Мы говорим, что товар 2 представляет композитный товар, воплощающий в себе все то, что хотел бы потребить данный потребитель, помимо товара 1. Что касается алгебраической формы бюджетного ограничения, уравнение (2.2) есть просто особый случай формулы, заданной уравнением (2.1), при р2 = 1, так что все то, что можно сказать о бюджетном ограничении вообще, будет верным и для трактовки товара 2 как композитного.
2.3. Свойства бюджетного множества
Бюджетная линия есть множество наборов, которые стóят в точности m:
p1x1 + p2x2 = m. |
(2.3) |
Это товарные наборы, на которые полностью расходуется весь доход потребителя.
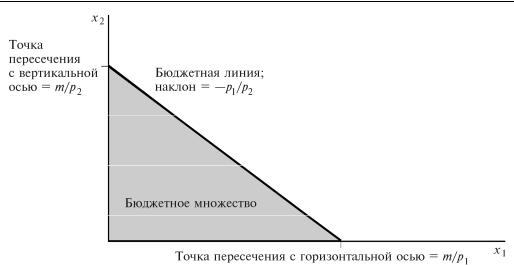
Бюджетное множество изображено на рис.2.1. Жирной линией изображена бюджетная линия — наборы, стóящие в точности m; а под этой линией располагаются наборы, которые стóят строго меньше m.
Бюджетное множество. Бюджетное множество состоит из всех наборов, дос- |
Рис. |
тупных при данных ценах и доходе. |
2.1 |
|
|
Можно преобразовать уравнение бюджетной линии в уравнение (2.3), что даст нам формулу
x2 |
= |
m |
— |
p1 |
x1. |
(2.4) |
|
p2 |
p2 |
||||||
|
|
|
|
|

38 Глава 2
Это формула для прямой, пересекающей вертикальную ось в точке m/p2 и имеющей наклон –p1/p2. Данная формула показывает, сколько единиц товара 2 должен потребить потребитель, чтобы при потреблении x1 единиц товара 1 бюджетное ограничение как раз удовлетворялось.
Приведем легкий способ нарисовать бюджетную линию при заданных ценах (p1, p2) и доходе m. Достаточно спросить себя, сколько товара 2 мог бы купить потребитель, если бы он истратил на него все свои деньги. Ответ: конечно, m/p2. Теперь спросите, сколько товара 1 мог бы купить потребитель, если бы он истратил на него все свои деньги. Ответ: m/p1. Таким образом, точки пересечения с горизонтальной и вертикальной осями показывают количества товаров, которые мог бы получить потребитель, если бы он истратил все свои деньги соответственно на товары 1 и 2. Чтобы провести данную бюджетную линию, достаточно нанести эти две точки на соответствующие оси графика и соединить их прямой линией.
Наклон бюджетной линии имеет красивую экономическую интерпретацию. Он показывает пропорцию, в которой рынок готов "заместить" товар 2 товаром 1. Предположим, например, что потребитель намерен увеличить свое потребление товара 1 на x1.1 Насколько должно измениться потребление товара 2 данным потребителем, чтобы его бюджетное ограничение удовлетворялось? Для обозначения изменения потребления товара 2 данным потребителем будем использовать x2.
А теперь заметим, что если данное бюджетное ограничение удовлетворяется и до, и после изменений, то тем самым должны удовлетворяться равенства
p1x1 + p2x2 = m.
и
p1 x1 x1 p2 x2 x2 m.
Вычитание первого уравнения из второго дает
p1 x1 + p2 x2 = 0.
Это уравнение показывает, что общая величина изменения потребления данного потребителя должна равняться нулю. Выразив из данного уравненияx2/ x1 — пропорцию, в которой товар 2 можно заместить товаром 1, не нарушая при этом бюджетного ограничения, получим
x2 = p1 .x1 p2
Это не что иное, как наклон бюджетной линии. Отрицательный знак стоит перед ним потому, что x1 и x2 всегда должны иметь противоположные знаки. Если вы потребляете больше товара 1, вам приходится потреблять меньше товара 2, и наоборот, чтобы заданное бюджетное ограничение по-прежнему удовлетворялось.
1 Запись x1 обозначает изменение количества товара 1. Более подробно про изменения и относительные изменения см. "Математическое приложение".
БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ |
39 |
Иногда экономисты говорят, что наклон бюджетной линии показывает альтернативные издержки потребления товара 1. Чтобы потребить больше товара 1, приходится отказаться от некоторой величины потребления товара 2. Отказ от возможности потребления товара 2 есть истинные экономические издержки большего потребления товара 1; и эти издержки измеряются наклоном бюджетной линии.
2.4. Как изменяется бюджетная линия
При изменении цен и дохода изменяется и множество товаров, доступное потребителю. Как влияют эти изменения на бюджетное множество?
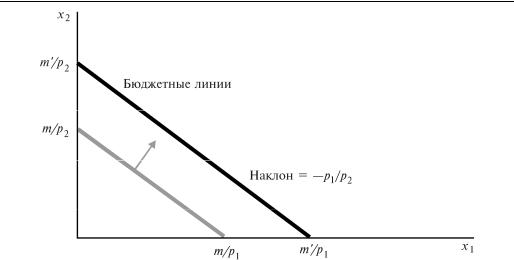
Вначале рассмотрим изменения дохода. Из уравнения (2.4) нетрудно увидеть, что возрастание дохода приведет к увеличению отрезка, отсекаемого бюджетной линией на вертикальной оси, не повлияв при этом на наклон этой линии. Таким образом, рост дохода будет иметь результатом параллельный сдвиг бюджетной линии вовне, как на рис.2.2. Аналогично, уменьшение дохода вызовет параллельный сдвиг бюджетной линии внутрь.
Возрастание дохода. Возрастание дохода вызывает параллельный сдвиг |
Рис. |
бюджетной линии наружу. |
2.2 |
|
|
40 |
Глава 2 |
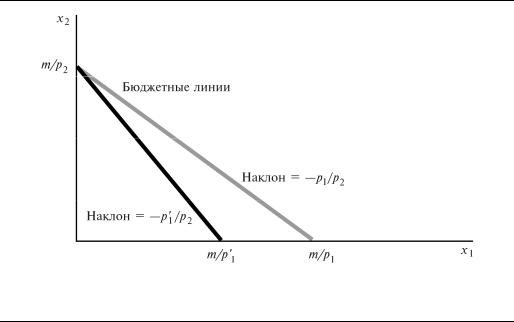
А что можно сказать об изменениях цен? Вначале рассмотрим возрастание цены товара 1, считая цену товара 2 и доход постоянными. Как видно из уравнения (2.4), возрастание p1 не изменит точки пересечения бюджетной линии с вертикальной осью, но сделает бюджетную линию круче, поскольку p1/p2 увеличится.
Другой способ посмотреть, как изменится бюджетная линия, состоит в том, чтобы прибегнуть к приему, описанному нами выше при проведении бюджетной линии. Если вы тратите все деньги на товар 2, то возрастание цены товара 1 не изменяет максимального количества товара 2, которое вы можете купить, следовательно, точка пересечения бюджетной линии с вертикальной осью не меняется. Но если вы тратите все деньги на товар 1 и он становится дороже, то потребление вами товара 2 должно сократиться. Следовательно, точка пересечения бюджетной линии с горизонтальной осью должна сдвинуться внутрь, в результате чего наклон бюджетной линии будет больше (рис.2.3).
Рис. Возрастание цены. Если товар 1 становится дороже, бюджетная линия ста-
2.3новится круче.
Что происходит с бюджетной линией при одновременном изменении цен товара 1 и товара 2? Предположим, например, что мы удваиваем цены обоих товаров. В этом случае и точка пересечения бюджетной линии с горизонтальной осью, и точка ее пересечения с вертикальной осью сдвинутся внутрь, причем координаты новых точек будут равны координатам прежних точек, умноженным на 1/2, и поэтому бюджетная линия сдвигается внутрь также с коэффициентом 1/2. Умножение обеих цен на два — то же самое, что деление дохода на 2.
Это можно выразить и алгебраически. Предположим, что наша исходная бюджетная линия есть

БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ |
41 |
p1x1 + p2x2 = m.
Предположим, далее, что обе цены возрастают в t раз. Умножение обеих цен на t дает
tp1x1 + tp2x2 = m.
Но это уравнение — то же самое, что и
p1x1 + p2x2 = m/t.
Таким образом, умножение обеих цен на постоянную величину t есть то же самое, что и деление дохода на эту постоянную величину t. Отсюда следует, что если умножить на t и цены обоих товаров, и доход, то бюджетная линия совсем не изменится.
Можно также рассмотреть одновременные изменения цен и дохода. Что произойдет, если цены обоих товаров возрастут, а доход снизится? Подумайте, что произойдет с точками пересечения бюджетной линии с горизонтальной и вертикальной осями. Если m уменьшается, а p1 и p2 растут, то соответствующие координаты обеих точек пересечения с осями m/p1 и m/p2 должны уменьшиться. Это означает, что бюджетная линия сдвинется внутрь. А что произойдет с наклоном бюджетной линии? Если цена товара 2 возрастет в большей степени, чем цена товара 1, так что
– p1/p2 уменьшится (по абсолютной величине), бюджетная линия станет более пологой; если же цена товара 2 возрастет в меньшей степени, чем цена товара 1, бюджетная линия станет более крутой.
2.5. Измеритель
Бюджетная линия определяется двумя ценами и одним доходом, но одна из этих переменных лишняя. Мы могли бы придать одной из цен или доходу некое постоянное значение и соответствующим образом изменить другие переменные так, чтобы получить в точности то же самое бюджетное множество. Таким образом, бюджетная линия
p1x1 + p2x2 = m
есть в точности та же бюджетная линия, что и
p1 x1 + x2 = m p2 p2
или
p1 x1 + p2 x2 = 1, m m
так как первая бюджетная линия получена делением всех членов уравнения на р2, а вторая — делением всех членов уравнения на m. В первом случае мы приравняли р2 к 1, а во втором — приравняли m к 1. Приравнивание цены одного из товаров или дохода к 1 и соответствующее изменение второй цены и дохода совершенно не изменяют бюджетного множества.
42 |
Глава 2 |
Когда мы приравниваем к 1 одну из цен, как это сделано выше, мы называем эту цену ценой-измерителем. Цена-измеритель — это цена, относительно которой мы измеряем цену другого товара и доход. Иногда бывает удобно считать один из товаров товаром-измерителем, поскольку тем самым изменение одной из цен исключается из рассмотрения.
2.6.Налоги, субсидии и рационирование
Вэкономической политике часто используются инструменты, оказывающие воздействие на бюджетное ограничение потребителя, скажем, налоги. Например, если правительство вводит налог на объем покупок, это означает, что потребитель должен платить правительству определенную сумму с каждой покупаемой им единицы товара. В США, например, потребители платят в виде федерального налога на бензин около 15 центов за галлон.
Как влияет налог на объем покупок на бюджетную линию потребителя? С точки зрения потребителя, налог — это то же самое, что и повышение цены. Следовательно, налог в t долларов на единицу товара 1 просто изменяет цену товара 1 с р1 на р1 + t. Как мы видели выше, это означает, что бюджетная линия должна стать круче.
Другой вид налога — налог на стоимость. Названием подразумевается, что им облагается стоимость — цена товара, а не купленное количество товара. Налог на стоимость обычно выражается в процентах. В большинстве штатов США действуют налоги с оборота. Если налог с оборота составляет 6%, то товар, оцениваемый в 1$, фактически продается за 1,06$. ( Налоги на стоимость называют также налогами ad valorem).
Если товар 1 имеет цену р1, но облагается налогом с оборота по ставке ,
то фактически для потребителя цена равна (1 + t)р1. Потребитель должен заплатить р1 поставщику и tр1 правительству за каждую единицу товара, так что общая стоимость товара для потребителя составит (1 + t)р1.
Субсидия — противоположность налога. В случае субсидии на объем покупок правительство дает потребителю сумму, размер которой зависит от купленного количества товара. Если бы, например, потребление молока субсидировалось, правительство выплачивало бы каждому потребителю молока некоторую сумму, зависящую от количества молока, покупаемого этим потребителем. Если бы субсидия составляла s долларов на единицу потребления товара 1, то, с точки зрения потребителя, цена товара 1 равнялась бы p1 – s. Это привело бы к тому, что бюджетная линия стала бы более пологой.
Аналогично, субсидия на стоимость (или долевая субсидия — прим. науч. ред.) есть субсидия, основанная на цене субсидируемого товара. Если правительство возвращает вам 1$ из каждых 2$, которые вы жертвуете на цели благотворительности, то ваши пожертвования на цели благотворительности субсидируются по ставке в 50%. Вообще, если цена товара 1 равна р1 и товар 1 субсидируется в форме долевой субсидии по ставке , то фактическая цена товара 1 для потребителя равна (1 — s)p1.
БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ |
43 |
Как видим, воздействие налогов и субсидий на цены совершенно одинаково, за исключением алгебраического знака: налог повышает цену для потребителя, а субсидия понижает ее.
Другой вид налога или субсидии, который может использоваться правительством, — аккордный налог или аккордная (недолевая) субсидия. В случае налога это означает, что правительство отбирает некую сумму денег, не зависящую от поведения индивида. Следовательно, введение аккордного налога означает, что бюджетная линия потребителя сдвинется внутрь, поскольку его денежный доход был сокращен. Аналогично, аккордная субсидия означает сдвиг бюджетной линии наружу. Налоги на объем покупок и налоги на стоимость в разной степени увеличивают крутизну бюджетной линии в зависимости от того, какой товар ими облагается, аккордный же налог всегда сдвигает бюджетную линию внутрь.
Иногда правительства вводят также нормирующие (рационирующие) ограничения. Это означает, что устанавливается некий уровень потребления какого-то товара, превышение которого запрещено. Например, во время Второй мировой войны правительство США нормировало потребление некоторых видов продуктов питания, таких, как масло и мясо.
Допустим, например, что вследствие нормирования товара 1 данный потре-
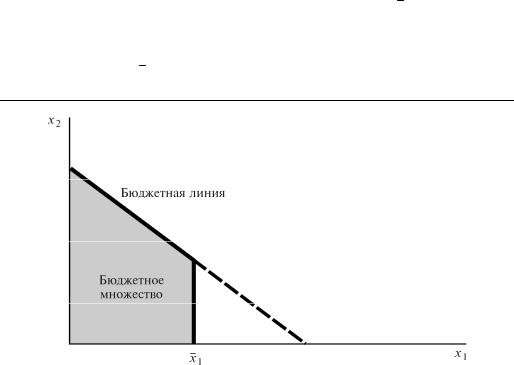
битель не может потреблять его в количестве большем, чем x 1. Тогда бюджетное множество для данного потребителя примет вид, изображенный на рис.2.4: оно будет представлять собой прежнее бюджетное множество, но с "отсеченным" куском. Этот "отсеченный" кусок состоит из всех наборов, которые доступ-
ны, но у которых x1 > x 1.
Бюджетное множество при нормировании потребления. Если потребление |
Рис. |
товара 1 нормируется, то часть бюджетного множества, выходящая за рамки |
2.4 |
