8. Независимые переменные механической смеси фаз для заданного состава системы

Однокомпонентная система

Рассмотрим однокомпонентную систему, состоящую из механической смеси из mфаз. Все фазы отличаются друг от друга агрегатным состоянием либо симметрией, но все образованы из одного и того же компонента. Механическая смесь в этом случае полностью характеризуется заданием фигуративной точки(γ₁,γ₂,..,γ_m), лежащей внутри правильного симплекса (cединичными ребрами), для долей фаз в пространстве размерности (m-1). Для долей фаз в смеси имеет место уравнениеγ₁+γ₂+…+γ_m=1. В качестве независимых переменных могут быть выбраны переменные γ₁,γ₂,..,γ_m-1 или, что эквивалентно предыдущему, барицентрические координаты точки Φ(γ₁,γ₂,..,γ_m) симплекса долей фаз.

Двухкомпонентная система.

Механическая смесь фаз полностью характеризуется долями, входящих в нее фаз и концентрациями компонентов в фазах. При фиксированном составе смеси, соответствующем точке M(C₁,C₂)правильного симплекса концентраций, не все доли фаз и концентрации в фазах являются независимыми. Для двухкомпонентной системы симплекс концентраций представляет собой концентрационный отрезок (рис.10).

Рассмотрим механическую смесь фаз в двухкомпонентной системе, состоящую из m фаз, составы которых определяются фигуративными точкамиA_j (j=1,2,...,m). Тогда фигуративную точку состава системы найдем из уравнений для центра масс системы точечных масс {γ_jA_j} (j=1,2,...,m),,С₁+С₂=1.

Состав системы может быть задан концентрацией второго компонента C₂.Составj-ой фазы будем задавать концентрацией второго компонента в системе(j=1,2,..,m).

О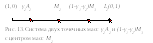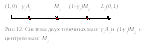пределим независимые переменные механической смеси фаз двухкомпонентной системы для фиксированного состава системы, то есть приC₂=const.

Зададим состав первой фазы, который определяется фигуративной точкой А₁. Тогда, используя теоремы о центре масс конечной системы точечных масс, можно записатьM₁=γ₁A₁+(1-γ₁)M₂, (76) гдеM₂центр масс системы точечных масс без первой точечной массы. . Для того, чтобы точкаМ₂была внутренней точкой симплекса концентраций, необходимо, чтобыили. (77) ТочкаL₁является точкой пересечения луча, направленного вдоль вектораA₁M₁ (A₁-начало,M₁- конец), с (гранью, ребром) вершиной симплекса концентраций рис.12.

Зададим фигуративную точку A₂, выполнив те же преобразования, как для фигуративной точкиA₁. ПолучимM₂=γ₂A₂+(1-γ₁+γ₂)M₃, (78) гдеM₃есть центр масс системы точечных масс без первой и второй точечной массы. Поскольку точкаM₃должна лежать внутри симплекса концентраций необходимо, чтобы выполнялось условиеили. (79) ТочкаL₁является точкой пересечения луча, направленного вдоль вектораA₁M₁, с (гранью) вершиной симплекса концентраций рис.13.

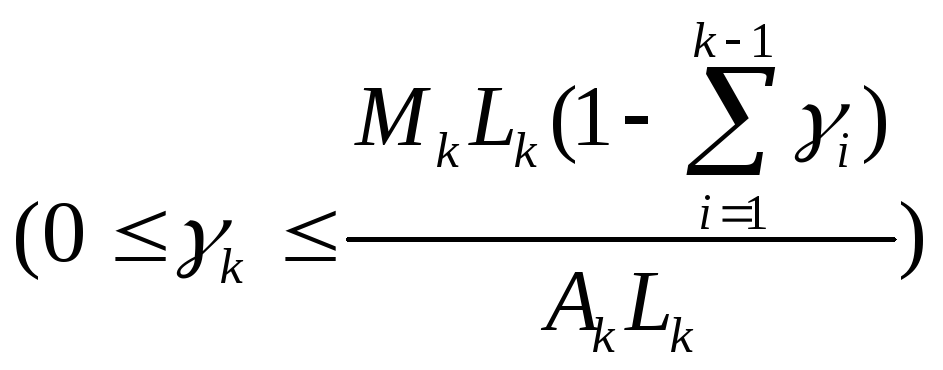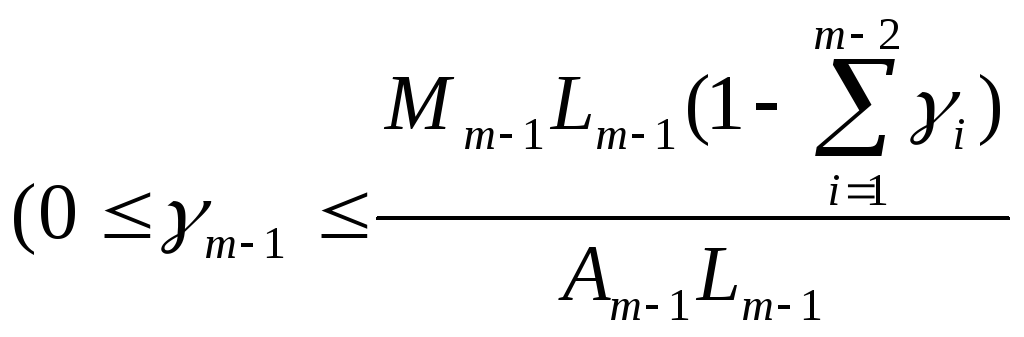Продолжая этот процесс для фигуративной точки A_k, получим, (80),(1≤k≤m-1). (81) На последнем этапеM_m≡A_m.M_m-центр масс системы, состоящей из одной точечной массы γ_mA_m, то есть последнее уравнение имеет вид ,.(82) . (83)

Из системы уравнений (80) и (82) следует, что в качестве независимых переменных механической смеси фаз можно выбрать (m-1) фигуративных точек состава фазA_i(i=1,2,..,m-1) и(m-1)значений долей фазγ_i (i=1,2,..,m-1). Число независимых переменных

для двухкомпонентной системы, представляющей механическую смесь из m фаз, равно2(m-1). Область определения независимых переменных для состава фазлежит в интервале (0≤≤1), а область определения доли фазγ_j определяется неравенствами (81) и (83). Если в смеси имеются фазы постоянного состава, то число независимых переменных в механической смеси, соответственно, уменьшается.

Алгоритм определения независимых переменных механической смеси фаз при фиксированном составе системы и расчета потенциала Гиббса.

На основе уравнений (80),(82) можно разработать итерационный алгоритм определения независимых переменных при фиксированном составе системы и определения области их определения.

1. j=1.

2. Задать фигуративную точку A_jв симплексе концентраций.

3. Построить луч A_jM_j и найти точку L_j пересечения луча с поверхностью симплекса концентраций.

4. Найти область определения γ_j и задать значение для доли фаз γ_j.

5. Вычислить центр масс M_j+1 для оставшейся системы точечных масс.

6. Если j<m-1 (число фаз в механической смеси), передать управление в 2.

7. Иначе A_m (фигуративная точка состава последней фазы) ^{присвоить M}_m ^{и .}

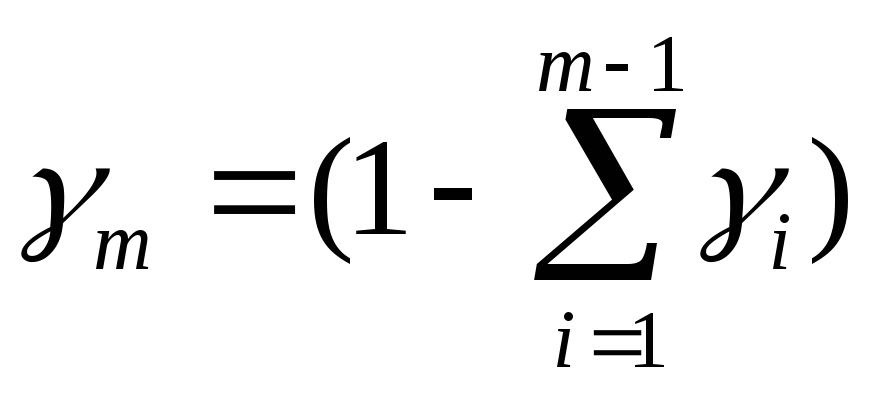8. Рассчитать потенциал Гиббса по формуле (61).

Примечание к алгоритму.

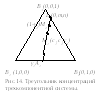Если в смеси имеются фазы постоянного состава, то они должны рассматриваться первыми. Алгоритм должен учитывать возможность существования фаз с ограниченной растворимостью компонентов. Все фазы должны быть разбиты на классы: фазы постоянного состава, фазы с ограниченной областью существования и фазы произвольного состава. В

соответствии с этим в алгоритм должны быть внесены соответствующие изменения.

Данный алгоритм остается неизменным и для многокомпонентных систем. Изменения касаются лишь того, что фигуративные точки, изображающие состав фаз, принадлежат симплексу концентраций, определенному в многомерном пространстве, а не на отрезке концентраций, как для двухкомпонентной системы.

Для примера рассмотрим трехкомпонентную систему с фиксированным составом, соответствующим фигуративной точке .Симплексом концентраций в этом случае служит равносторонний треугольник с единичными ребрами (пространство двумерно).

Вершины треугольника концентраций выберем в качестве базиса барицентрических координат. Обозначим эти вершины точками B_i (1i3), тогда действительные величиныC_1,C₃C₃при условииявляются барицентрическими координатами единственной собственной точкиM₁. Если 0C_j (j=1,2,3), то точкаM_jлежит внутри координатного симплекса и может представлять состав системы или некоторой фазы. Вершины координатного симплекса имеют координатыB₁(1,0,0),B₂(0,1,0),B₃(0,0,1). ТочкаL₁, лежащая на ребреB₂B₃, имеет барицентрические координатыL₁(0,m,n), гдеm0 иn0, (m+n=1). Эти точки делят ребро в отношенииB₂L₁/L₁B₃=n/m. ТочкаL₁ является центром масс системы из двух точечных массmB₂иnB₃,.то есть имеет место выражениеL₁= (mB₂+nB₃)/(m+n). Если задать декартовы координаты вершин треугольника, то по формуле центра масс легко получить и декартовы координаты фигуративных точек состава фаз, и, следовательно, вычислить длины отрезковM₂L₁, A₂L₁, знание которых необходимо при реализации рассмотренного выше алгоритма расчета потенциала Гиббса. Ситуация, представленная на рис.14 для трехкомпонентной системы, для двухкомпонентной системы изображена на рис.12. Зададим в треугольнике концентраций фигуративную точкуA₁, соответствующую составу первой фазы. Центр масс оставшейся системы точечных масс должен лежать на прямой линии, проходящей через точкиA₁и M₁. Состав смеси фаз без одной фазы должен лежать внутри концентрационного треугольника на указанной линии, то есть на отрезкеM₁L₁. Из этого требования получатся ограничения на долю первой фазы - выражение (77), ранее полученное для двухкомпонентной системы. Повторяя для трехкомпонентной системы весь алгоритм, выполненный ранее для двухкомпонетной системы, получим записи (80),(81),(82), (83), но для трехкомпонентной системы. В этом случае фигуративные точки состава должны браться в треугольнике концентраций. Если предположить, что в многомерном пространстве (с числом измерений больше трех) центр масс конечного числа точечных масс так же единственен, то указанный алгоритм определения независимых переменных и вычисления потенциала Гиббса многокомпонентных систем будет справедлив и для систем с числом компонентов больше четырех.

Минимумы механической смеси фаз по независимым переменным определят стабильные или метастабильные состояния системы. Используя итерационную процедуру нахождения областей определения независимых переменных, несложно разработать и процедуры минимизации потенциала Гиббса для механической смеси фаз. Рассматриваемая задача по своей проблематике сходна с задачами линейной оптимизации, когда экстремум функции необходимо найти при условии целого ряда ограничений на область определения переменных функции и существования связей между переменными. В данном случае области определения независимых переменных γ зависят от значений составов фаз. Поэтому обычные методы минимизации функции многих переменных неприменимы для задачи минимизации механической смеси фаз при фиксированном составе системы.

При практическом решении задачи становится важным, какие фазы включить в механическую смесь фаз, а какие можно не включать без ущерба для корректности решения. Помощь в этом могут оказать диаграммы основных состояний, то есть рассмотрение конкуренции фаз при температуре абсолютного нуля. В этом случае конкуренция фаз определяется полностью их внутренней энергией.