Алгоритм решения уравнений материального баланса.

1. Сформировать таблицу типа (69), определяющую структуру распределения вещества по фазам, возможным в системе.

2. Получить уравнения типа (70).

3. Выразить зависимые переменные через независимые переменные.

Только выполнение первого пункта алгоритма содержит творческие элементы. Пункты 2 и 3 формализованы и легко могут быть запрограммированы и оставаться без каких либо изменений при решении задач для разных систем.

Если в смеси фаз имеются фазы постоянного состава, то с ними связывается только одна переменная  - доля этой фазы. Вклад этой фазы в уравнения системы (62) удобно сразу располагать в правой части системы уравнений (59), поскольку состав этой фазы известен и постоянен, а связанная с ней переменнаяна каждом этапе минимизации известна. В систему уравнений (62) эта фаза не вносит никаких изменений.

Таким образом, появление в смеси фаз постоянного состава не меняет ни схему выбора свободных переменных, ни алгоритм решения системы линейных уравнений (58),(59) и (62).

Если в системе рассматривается число фаз больше двух или число возможных компонентов больше двух, то при минимизации может возникнуть осложнение, связанное с возможностью нарушения неравенств в выражениях (58),(57) и (60). Процедура минимизации выражения (61) по свободным переменным, областью определения которых является симплекс фаз и симплекс концентраций, имеет ряд особенностей по сравнению с обычной минимизацией функций.

Необходимо задать алгоритм, обеспечивающий выполнение неравенств в процессе минимизации потенциала Гиббса (61). Это можно сделать разными способами: либо постоянным переопределением областей изменения переменных, либо перенормировкой значений переменных. Пусть на некотором шаге минимизации переменные имеют значения, удовлетворяющие условию (58), и некоторое(l), имевшее значение(l)=_old, принимает новое значение(l)=_new. Для того, чтобы выполнялось равенство (57) и не нарушались неравенства для, нормируем(i) при (il)

_{. (71)}

Как следует из выражения (71) изменение доли фазы lпроисходит за счет уменьшения или соответствующего увеличения долей других фаз. При этом, если для какой либо фазы_old=0, то ее доля не может уменьшиться при изменении доли фазы(l) . Поэтому ни у одной фазы при использовании (71) не может получиться значения меньше нуля. Поскольку все величиныв (71) больше нуля, то. Подставляя в правую часть последнего выражения из (71), получимили.

Таким образом, если при изменении _lодновременно переопределить доли остальных фаз в соответствии с (71), то это гарантирует выполнение неравенств (57).

Аналогично тому, как строится правильный симплекс концентраций для геометрического изображения состава фазы, можно построить правильный симплекс для долей фаз механической смеси. Назовем его симплексом фаз. Вершинам симплекса соответствуют однофазные состояния системы. Ребрам соответствуют двухфазные смеси. Граням - трехфазные состояния системы. Гиперграням n-го порядка будут соответствовать смеси изnфаз.

Равновесным состояниям стабильным или метастабильным, при фиксированных термодинамических параметрах давлении P, температуреTи средних концентраций компонентов {C_i} будут соответствовать фигуративные точки симплекса фаз. В соответствии с правилом фаз Гиббса не может быть равновесных состояний на гипергранях порядка выше, чемk+2. Таким образом, в состоянии равновесия при фиксированных термодинамических параметрах в конкуренции фаз могут принять участияmфаз, соответствующих вершинам симплекса фаз. Количество возможных двухфазных равновесных состояний, участвующих в конкуренции равно числу ребер симплекса равно числу сочетаний_{. Число трехфазных состояний, участвующих в}конкуренции, равно числу гиперграней 3-го порядка- числу сочетаний из (m-1) по 3. Число гиперграней с максимально возможным порядком гиперграниk, на которой_{может находиться фигуративная точка, равно}числу сочетаний из (m-1) поk. Максимальное число равновесных состояний, которое может участвовать в конкуренции, равно. Точки, лежащие на гепергранях правильного симплекса фаз, порядка вышеk+2 не могут содержать состояний, которые бы соответствовали равновесию фаз друг с другом, так как в равновесии число фаз должно удовлетворять правилу фаз Гиббса. Если на геперграни имеется фигуративная точка, соответствующая состоянию равновесия, то это состояние может быть или стабильным, или метастабильным. Таким образом, чтобы получить полную информацию о возможных равновесных состояниях системы, нужно перебрать все возможные комбинации фаз, удовлетворяющие правилу фаз Гиббса при данных термодинамических условиях. Число таких состояний системы не превосходит числа гиперграней симплекса фаз. Все эти состояния можно определить, последовательно перебирая термодинамические потенциалы Гиббса (61) для гиперграней, начиная с гиперграней низшего порядка.

Хотя выражение (71) гарантирует выполнение неравенств (57) и (62), оно не позволяет полностью оптимизировать процесс минимизации потенциала (61), поскольку предполагает увеличение или уменьшение l-ой фазы за счет всех других фаз, а не за счет наиболее невыгодной фазы. Вместе с тем, положительным моментом в (71) является постоянное изменение направления движения фигуративной точки в пространстве правильного симплекса долей фаз. Это гарантирует, что глубокая "ложбина", "овраг" при численной минимизации не будет принят за минимум термодинамического потенциала.

Если мы хотим произвольно менять направление движения фигуративной точки в пространстве симплекса долей фаз, то следует использовать метод, аналогичный методу, развитому для дифференцирования вдоль луча, выходящего из l-ой вершины симплекса состава [5].

Набор переменных , для которых имеется одна связь, можно заменить на набором из (m-1) независимых переменных. Зависимая переменная_m выражается через_lи безразмерные величины_k,m

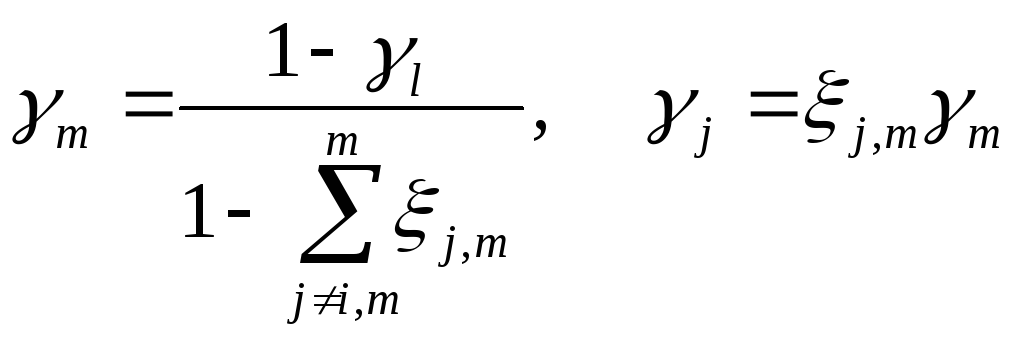_{. (72)}

Изменение величины _l, проводится при фиксированных значения переменных_j,m. После изменения переменной_lвыполняется переход к переменным. Таким образом, получим

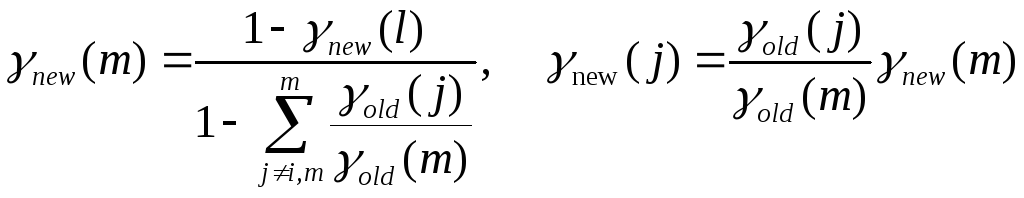_{(j≠m≠l, j≠l).(73)}

Способ изменения доли фазы _l, определяемый выражением (73), предполагает изменение доли фазыlза счет долей других фаз при фиксированных отношениях долей этих фаз к доле произвольно выбранной фазы, для которой0. Это соответствует изменению долей фаз при движении фигуративной точки вдоль луча, выходящего изlвершины симплекса.

Для независимых переменных, описывающих состав многокомпонентных фаз, имеют место аналогичные (73) уравнения _{, (74) где kl – число компонентов в l – ой фазе, k,n,j – номера компонентов в фазе с номером l (k≠n≠l, k≠l). k- произвольно выбранный компонент в l – фазе.}

Кроме сложностей минимизации, связанных с обеспечением выполнения неравенств в (57) (60), при минимизации (61) имеется еще одна проблема, связанная с тем, что в процессе минимизации для некоторых фаз, не выдержавших конкуренции с другими фазами, при данных термодинамических условий _l=0.

Это соответствует переходу фигуративной точки в симплексе фаз на гипергрань более низкого порядка, но такой переход сопровождается скачкообразной заменой уравнений материального баланса и сменой независимых переменных. Хотя вывод уравнений материального баланса и выбор независимых переменных в достаточной степени формализован и может быть встроен в процедуру минимизации термодинамического потенциала механической смеси фаз (61), однако разработка алгоритма минимизации для произвольной общей абстрактной термодинамической системы становится достаточно сложной. Если все фазы в выражении (61) в данных термодинамических условиях устойчивы и ни одна из фаз не исчезает, проблем не возникает (в системе не предполагается химических реакций между компонентами). Если же некоторые фазы исчезают, то в ряде случаев могут возникнуть осложнения с выбором независимых переменных из-за специфичности системы. Так, если в рассматриваемом выше примере (69), доля первой фазы ₁обратится в нуль, то переменные₁,₂уже не могут быть независимыми, поскольку в дополнение к уравнению на доли фаз (68) возникает дополнительное уравнение, возникновение которого обязано запретом на растворимость третьего компонента во второй фазе. Из этих трех переменных в данной ситуации может быть независимой только одна переменная типа. В конкретных случаях такие ситуации легко анализируются. Они могут быть учтены в алгоритме, но нет гарантий, что не возникнут еще какие-нибудь новые ситуации. Поэтому попробуем создать иной алгоритм минимизации, в котором не возникало бы необходимости контролировать смену систем уравнений материального баланса и обеспечивать выполнение неравенств в выражениях (57) и (60). Предварительно этому рассмотрим более подробно описание состава многокомпонентных систем и барицентрические координаты.