6. Графическое изображение состава многокомпонентной системы

Состав двухкомпонентной системы графически может быть изображен единичным отрезком прямой. Независимая переменная в этом случае одна. В качестве независимой переменной выберем концентрацию второго компонентаC₂и будем откладывать ее вдоль оси концентрации. Концентрация первого компонента в системе равнаC₁=1-C₂.

Состав трехкомпонентной системы изображается треугольником концентраций. В этом случае имеется две независимые переменные C₃ и C₂. Состав первого компонента вычисляется из уравненияС₁=1- C₂ – C₃. Состав трехкомпонентной системы изображается равносторонним треугольником. Вершинам треугольника приписывается смысл фигуративных точек чистых веществ. Фигуративным точкам, лежащим на сторонах треугольника, приписывается смысл двухкомпонентных систем. Точкам, лежащим внутри треугольника, приписывается смысл тройной системы. Фигуративной точкеX, лежащей внутри треугольника, соответствует состав в соответствии с рис.11.

Д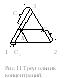ля определения концентрации компонентов проводим через точкуXлинии, параллельные сторонам треугольника, до пересечения их со сторонами. Длине отрезка [1C₂] соответствует концентрация второго компонентаС₂. Длине отрезка [2C₃] соответствует концентрация третьего компонентаС₃. Длине отрезка [3C₁] соответствует концентрация первого компонентаС₁.

Для графического изображения четырехкомпонентных систем используется единичный тетраэдр. Для описания систем, состав которых выше четырех, _lиспользуются понятия многомерного пространства независимых переменныхC_i. В этом пространстве фигуративные точки состава многокомпонентной системы образуют многомерную фигуру – правильный симплекс.

Симплексом называется многомерная фигура, содержащая наименьшее количество ребер в пространстве данного измерения. Правильным симплексом называется симплекс, у которого все ребра одинаковой длинны и все грани и гиперграни любого порядка тождественны по форме и размерам.

Размерность симплекса концентраций равна числу независимых концентраций. Грани первого порядка симплекса – это точки вершин симплекса, соответствующие чистым компонентам. Грани второго порядка это линии концентраций. Грани третьего порядка представляют треугольники концентраций и т.д.

Фигуративной точке правильного симплекса концентраций соответствует состав системы с концентрациями, равными барицентрическим координатам этой точки относительно вершин симплекса.

7. Барицентрические координаты

Определение[9]. Точку M, в которую помещена массаm, будем называть точечной массой, и будем писатьmM.

Определение. Под произведением точечной массы mMна положительно числоnбудем понимать точечную массу nmM.

Перечислим несколько аксиом для точечных масс [9].

Пусть имеется множество точек A,B,C,…..и множество точекa,b,c,…….

1. Если mPи nQдве точечные массы, то существует единственная точечная масса (m+n)R, называемая суммой данных точечных масс:mP+nQ=(m+n)R.ТочкаRназываетсяцентром масссистемыmPи nQ.

2. Для точечных масс справедлив коммутативный закон сложения, т.е. nQ + mP= mP+nQ=( m+n)R.

3. Для точечных масс справедлив ассоциативный закон сложения, т.е. mP+(nQ+rR)= (mP+nQ)+rR.

4. nP + mP=(n+m)P

5. k(mP+nQ)=kmP+knQ (распределительный закон сложения точечных масс относительно умножения на число).

6. Существует одно и только одно решение уравнения mP=nQ+xX, гдеm>n. Очевидно, чтоx=(m-n).

Определение. Решение уравнения mP=nQ+xXназывается разностью точечных масс и обозначаетсяxX= mP-nQ.

На основании аксиом1,2,3 доказывается следующие положение:

Любая конечная система точечных масс имеет единственный центр масс.

Определение. Будем говорить, что точка С находится между точкамиA иB, если существуют такие положительные числаmиn,чтоmA+nB=(m+n)C.

Из этого определения следует правило рычага

AC/CB=n/m.

Положительные числа m, nназываются барицентрическими координатами точкиC(m,n)относительно точекAиB. ТочкаCделит отрезок в отношенииn/m. Вершины отрезка в барицентрических координатах имеют видA(1,0), B(0,1).Если длина отрезкаAB равна единице иm+n=1, то отрезок легко отождествить с координатной осью. ТочкеС (центр масс системыmA+nB) соответствует точкаC₂=n,рис.10.

Возьмем треугольник ABC и три числаa,b,cтаких, чтоa+b+c=1. ТогдаaA+bB+cC есть определенная точкаM:M=aA+bB+cC, a+b+c=1. (75)

Обратно, любая точка плоскости ABC может быть единственным образом записана в виде (75).

Числа (a,b,c) в равенстве (75) называются барицентрическими координатами точки M относительно вершин треугольника.

Треугольник ABC называется координатным. Напомним, что точкаM есть центр масс трех точечных массaA, bB, cC.

Вершины треугольника имеют следующие барицентрические координаты: A(1,0,0),B(0,1,0),C(0,0,1).Точки, лежащие на отрезкеAB, имеют барицентрические координаты(m,n,0), где m≥0 иn≥0, (m+n=1).

Легко видеть, что точка M(C_A,C_B,C_C)=C_AA+C_BB+C_cC, являющаяся центром масс системы из трех точечных масс, расположенных в вершинах треугольника, (C_A+C_B+C_c=1) совпадает с точкойX, изображающей состав трехкомпонентной системы на концентрационном треугольнике рис.11.

Барицентрические координаты точек M(C_A,C_B,C_C), лежащих внутри треугольника концентраций, равны концентрациям трехкомпонентной системы, а точкаMпредставляет центр масс (центр тяжести системы) системы точечных масс {C_AA,C_BB_,C_CC},.

Составу многокомпонентной фазы с номером jв симплексе концентраций соответствует фигуративная точка. Если в уравнениях материального баланса (62)γ_l доли фаз интерпретировать как точечные массы, расположенные в точкахA_j, то эти уравнения можно трактовать, как систему уравнений для центра масс системы точечных масс {γ₁A,γ₂A,..,γ_mA}.

Барицентрическими координатами точек A_j(C_1,j,C_2,j,…C_k,j) служат концентрации фаз компонентов. Состав системы определяется выражением.