6.9. Формулы и таблицы для истинных и средних теплоемкостей. Определение количества теплоты по теплоемкости и разности температур

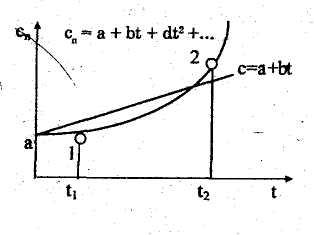На основании опытных данных установлено, что зависи­мость истинной теплоемкости реальных газов от температуры является криволинейной, как показано на рис. 6.6, и может быть выражена степенным рядом с_п= а + bt + dt ² +ef ³+ .... (6.34)

где а, 6, d,... постоянные ко­эффициенты, численные зна­чения которых зависят от рода газа и характера протекания процесса. В тепловых расчетах часто заменяют нелинейную зависимость теплоемкости от температуры линейной.

В этом случае истинная теплоемкость определяется из

уравнения (6.35)

где t — температура, °С; b=dc/dt–угловой коэффициент наклона прямой с_n = а + bt.

Исходя из (6.20), найдем формулу средней теплоемкости при ее линейном изменении от температуры согласно (6.35)

(6.36)

В случае, если процесс изменения температуры протекает в

интервале О-t , то (6.36) принимает вид(6.37)

Теплоемкость называют теплоемкостью средней в

интервале температур а теплоемкость

— теплоемкостью средней в интервале 0—t.

Результаты расчетов истинной и средней в интервале температур О—t массовой или мольной теплоемкостей при

постоянном объеме и давлении соответственно по уравнениям (6.34)и (6.37) приведены в справочной литературе. Основной тепло- и хладотехнической задачей является оп­ределение теплоты, участвующей в процессе. В соответствии с соотношением q =c_ndT и при нелинейной зависимости ис­тинной теплоемкости от температуры количество теплоты оп­ределяется заштрихованной элементарной площадкой на ди­аграмме с координатами с_nТ (рис. 6.6). При изменении темпе­ратуры от Т₁ до Т₂ в произвольном конечном процессе количе­ство подводимой или отводимой теплоты определяется, согласно (6.38), следующим образом:

(6.38)

и определяется на той же диаграмме (рис. 6.6) площадью 12T₂T₁1. Подставив в (6.38) значение с_n=f(T) для данного газа по соотношению (6.34) и произведя интегрирование, получим рас­четную формулу для определения теплоты в заданном интер­вале изменения температуры газа, которая, впрочем, следует из (6.16):

Однако, поскольку в справочной литературе есть только средняя теплоемкость в интервале температур 0—t, то количест­во теплоты в процессе 12 можно определить не только по преды­дущей формуле, но итак: Оче­видно соотношение между теплоемкостями средними в интер­валах температур T₁—T₂ и 0-t:

Количество теплоты, подводимое (отводимое) к m кг рабо­ чего тела

Количество теплоты, подводимое к V м³ газа, определяется формулой

Количество теплоты, подводимое (отводимое) к н молям рабочего тела, равно

6.10Молекулярно-кинетическая теория теплоемкости

Молекулярно-кинетическая теория теплоемкости является весьма приближенной, так как не рассматривает колебатель­ной и потенциальной составляющих внутренней энергии. По­этому, согласно этой теории, задача состоит в определении рас­пределения подводимой к веществу тепловой энергии между поступательной и вращательной формами внутренней кинети­ческой энергии. Согласно распределению Максвелла-Больцмана, если системе очень_ большого числа микрочастиц сооб­щить некоторое количество энергии, то она распределяется

между поступательным и вра­щательным движением микро­частиц пропорционально их числу степеней свободы. Число степеней свободы молекулы газа (п. 5.4) соответствует числу ко­ординат, определяющих ее по­ложение в пространстве.

Молекула одноатомного газа имеет три степени, свободы, так как ее положение в простран­стве определяется тремя координатами, причем для одноатом­ного газа эти три степени свободы являются степенями свобо­ды поступательного движения.

Для двухатомного газа значения трех координат одного атома еще не определяют положение молекулы в простран­стве, так как после определения положения одного атома не­обходимо учитывать, что второй атом имеет возможность вра­щательного движения. Для определения положения в простран­стве второго атома необходимо знать две его координаты (рис. 6.7), а третья же определится из известного в аналитической геометрии уравнения

где — расстояние между атомами. Таким образом, при изве­стном из шести координат необходимо знать только пять. Следовательно, молекула двухатомного газа имеет пять степе­ней свободы, из которых три — поступательного и две — вра­щательного движения.

Молекула трехатомного газа имеет шесть степеней свободы — три поступательного и три вращательного движения. Это следует из того, что для определения положения в пространстве необходимо знать шесть координат атомов, а именно: три координаты первого атома, две координаты второго атома и одну координату третьего. Тогда положение атомов в пространстве будет полностью определено, так как расстояния между ними - заданы.

Если взять газ большей атомности, то есть 4-атомный и более, то число степеней свободы такого газа будет равно так­же шести, так как положение четвертого и каждого следую­щего атома будет определяться фиксированным расстоянием его от других атомов.

Согласно молекулярно-кинетической теории вещества, сред­няя кинетическая энергия поступательного и вращательного движений каждой из молекул пропорциональна температуре

и равна соответственнои — число степеней сво­боды вращательного движения). Поэтому кинетическая энер­гия поступательного и вращательного движений всех молекул будет линейной функцией температуры

Дж, (6.39)

(6.40)

Дж.

Уравнения (6.39) и (6.40) выражают упомянутый закон равнораспределения энергии по степеням свободы, согласно которому на каждую степень свободы поступательного и вра­щательного движений молекул приходится одна и та же сред­няя кинетическая энергия, равная 1/2 (кТ).

Энергия колебательного движения молекул представляет собой сложную возрастающую функцию температуры и толь­ко в отдельных случаях при высоких температурах может быть приближенно выражена формулой, аналогичной (6.40). Моле­кулярно-кинетическая теория теплоемкости не учитывает ко­лебательного движения молекул.

Между двумя молекулами реального газа действуют силы отталкивания и притяжения. Для идеального газа потенциаль­ная энергия взаимодействия молекул отсутствует. С учетом изложенного внутренняя энергия идеального газа равна U=.Так как N=vnN_A ,то Внутренняя энергия одного моля идеального газа при условии, что универсальная газовая постоянная определя­ется произведением двух констант: = kN_A, определяется следующим образом:,Дж/моль.

Продифференцировав по Т и зная, что du/dT = c_r, получим моль­ную теплоемкость идеального газа при постоянном объеме

Коэффициент 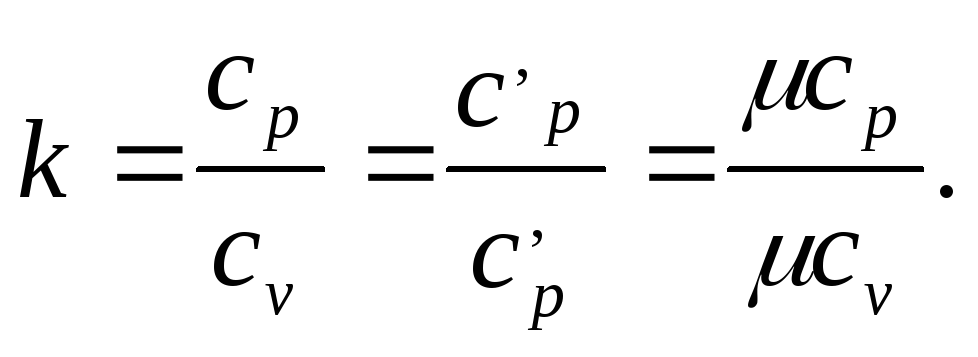называетсякоэффициентом Пуассона или показателем адиабаты.

Для идеального газа показатель адиабаты является вели­чиной, зависящей только от атомного строения молекул газа, что и отражено в табл. 6.1. Символическое значение показате­ля адиабаты можно получить из уравнения Майера с_p — c_v = R путем следующих преобразований: kc_v — c_p = R, c_v(k-l) - R, откудa к = 1 + R/c_v. Из предыдущего равенства следует выра­жение изохорной теплоемкости через показатель адиабаты cv = =R/(k—1) и затем изобарной теплоемкости: с_р.= kR/(k— 1).

Из уравнения Майера с_р = получим выражение для мольной теплоемкости идеального газа при постоянном давлении , Дж/(моль-К).

Для приближенных расчетов при не очень высоких темпе­ратурах, когда энергию колебательного движения атомов в молекулах вследствие ее малости можно не учитывать, допус­каются к использованию полученные мольные теплоемкости с_vис_p как функции атомности газов. Значения теплоемкостей представлены в табл. 6.1.

Таблиц6.1

Значения теплоемкостей по молекулярно-кинетической теории газов

теплоемкость Атомность газа					k
	кал	Дж	кал	Дж
	моль-град	моль-К	моль-град	моль-К
Одноатомный газ Двухатомный газ Трех- и более атомный газ	3 5 7	12,5 20,8 29,1	5 7 9	20.8 29.1 37.4	1,67 1,40 1,28