Broadband Packet Switching Technologies

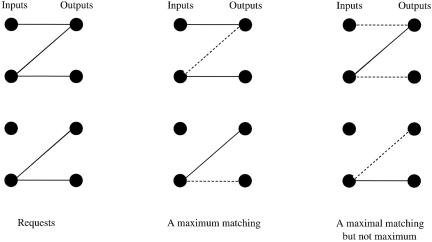
56 INPUT-BUFFERED SWITCHES

Fig. 3.5 A maximum matching and a maximal matching. Dotted lines represent the request pairs not in the matching.

A maximum matching is one that matches the maximum number of inputs and outputs, while a maximal matching is a matching where no more matches can be made without modifying the existing matches. See Figure 3.5 for an example.

The definition of stable matching assumes there is a priority list for each input and for each output. An input priority list includes all the cells queued at the input, while an output priority list concerns all the cells destined for the output Žalthough some of them are still waiting at inputs.. A matching is said to be stable if for each cell c waiting in an input queue, one of the following conditions holds:

1.Cell c is part of the matching, i.e., c will be transferred from the input side to the output side during this phase.

2.A cell that is ahead of c in its input priority list is part of the matching.

3.A cell that is ahead of c in its output priority list is part of the matching.

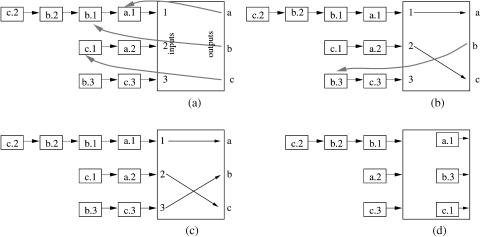
Conditions 2 and 3 may be simultaneously satisfied, but condition 1 excludes the other two. Figure 3.6 illustrates how the matching algorithm works for a 3 3 switch w32x. The letter in each cell denotes the output port where the cell should be forwarded, while the number denotes its order in the preference list of that output. The light arrows indicate the requests made by outputs, while the dark arrows represent the requests granted by inputs. During the first iterations each output asks for its most preferred cell enqueued at the inputs wsee Figure 3.6Ža.x. In turn, input 2 grants the only

Fig. 3.6 Example to illustrate a stable matching for a 3 3 switch.

request it receives to output c, while input 1 grants the request corresponding to its most preferred cell Ži.e. the request issued by output a for cell a.1..

Thus, after the first iteration, outputs a and c are matched to their most preferred cells. During the next iteration, the unmatched output port b requests its most preferred cell from input 2 3 wsee Figure 3.6Žb.x. As a result, input 3 grants the output b’s request and the matching completes. Figure 3.6Žd. shows the switch’s state after cells are transferred according to the resulting matching.

3.3 SCHEDULING ALGORITHMS

The arbitration process of a switch decides which cells at input buffers will be transferred to outputs. In the distributed manner, each output has its own arbiter, and operating independently from the others. An arbitration scheme decides which information should be passed from inputs to arbiters, and based on that information, how each output arbiter picks one among all input cells destined for the output.

An arbitration scheme is essentially a service discipline that arranges the service order among the input cells. We have three basic arbitration approaches: random selection, FIFO, and round-robin. In random selection, a cell is randomly selected among those cells. The FIFO arbitration picks the oldest cell. The slightly more complicated round-robin scheme is widely used because of its fairness. Inputs are numbered, say from 1 to N. Each output

consider this input in the current iteration.

58 INPUT-BUFFERED SWITCHES

input i q 1 has the highest priority to be granted access in the next round. If input i q 1 is idle in the next round, then input i q 2 has the highest priority, and so on so forth.

In some simple approaches, only essential information is exchanged between inputs and outputs: an input informs an output whether it has a cell for the output, and an output tells whether that cell is granted access. Some additional parameters, such as priority and timestamp, can be used to enhance the arbitration efficiency.

3.3.1 Parallel Iterative Matching (PIM)

The PIM scheme w2x uses random selection to solve the contention in inputs and outputs. Input cells are first queued in VOQs. Each iteration consists of three steps. All inputs and outputs are initially unmatched, and only those inputs and outputs that are not matched at the end of an iteration will be eligible to participate in the next matching iteration. The three steps in each iteration operate in parallel on each input and output as follows:

1.Each unmatched input sends a request to every output for which it has a queued cell.

2.If an unmatched output receives multiple requests, it grants one by randomly selecting a request over all requests. Each request has equal probability to be granted.

3.If an input receives multiple grants, it accepts one by randomly selecting an output among them.

It has been shown that, on average, 75% of the remaining grants will be matched in each iteration. Thus, the algorithm converges at OŽlog N . iterations. Because of the random selection, it is not necessary to store the port number granted in the previous iteration. However, implementing a random function at high speed may be too expensive.

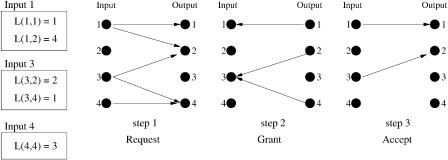
Fig. 3.7 An example of parallel iterative matching. LŽ x, y. s z means that there are z cells on the VOQ from input x to output y.

Fig. 3.8 An example of iRRM Žsame input cell distribution as in PIM..

60 INPUT-BUFFERED SWITCHES

Figure 3.7 shows how PIM works. Under uniform traffic, PIM achieves 63% and 100% throughput for 1 and N iterations, respectively.

3.3.2 Iterative Round-Robin Matching ( iRRM)

The iRRM scheme w23x works similarly to PIM, but uses the round-robin schedulers instead of random selection at both inputs and outputs. Each arbiter maintains a pointer pointing at the port that has the highest priority. Such a pointer is called the accept pointer ai at input i or the grant pointer gj at output j. The algorithm is run as follows:

1.Each unmatched input 3 sends a request to every output for which it has a queued cell.

2.If an unmatched output receives any requests, it chooses the one that appears next in a round-robin schedule, starting from the highest-prior-

ity element. The output notifies each input whether or not its request was granted. The pointer gi is incremented Žmodulo N . to one location beyond the granted input.

3.If an input receives a multiple grant, it accepts the one that appears

next in its round-robin schedule, starting from the highest-priority element. Similarly, the pointer aj is incremented Žmodulo N . to one location beyond the accepted output.

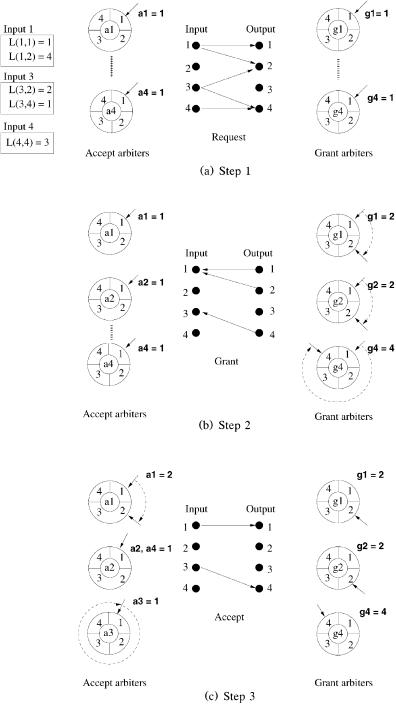
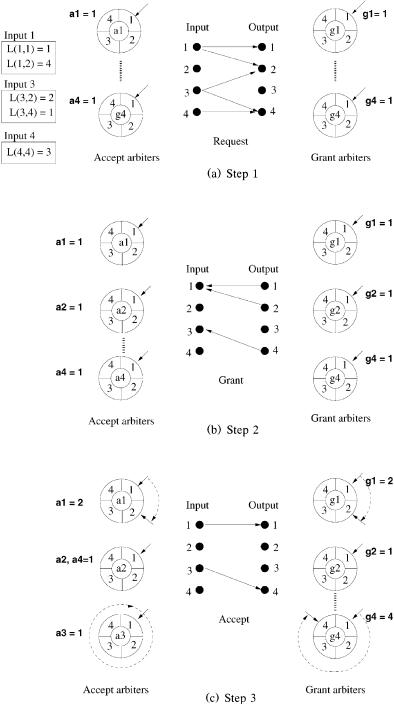
An example is shown in Figure 3.8. In this example, we assume that the initial value of each grant pointer is input 1 Že.g., gi s 1.. Similarly, each accept pointer is initially pointing to output 1 Že.g., aj s 1.. During step 1, the inputs request transmission to all outputs that they have a cell destined for. In step 2, among all received requests, each grant arbiter selects the requesting input that is nearest to the one currently pointed to. Output 1 chooses input 1, output 2 chooses input 1, output 3 has no requests, and output 4 chooses input 3. Then, each grant pointer moves one position beyond the selected one. In this case, g1 s 2, g2 s 2, g3 s 1, and g4 s 4. In step 3, each accept pointer decides which grant is accepted, as the grant pointers did. In this example, input 1 accepts output 1, and input 3 accepts output 4, then a1 s 2, a2 s 1, a3 s 1, and a4 s 1. Notice that the pointer a3 accepted the grant issued by output 4, so the pointer returns to position 1.

3.3.3 Iterative Round-Robin with SLIP( iSLIP)

An enhanced scheme ŽiSLIP. was presented in w24, 25x. The difference is that in this scheme, the grant pointers update their positions only if their grants are accepted. In this scheme, starvation is avoided because a recently matched pair gets the lowest priority. The steps for this scheme are as

3At the beginning each input is unmatched.

Fig. 3.9 iSLIP example.

62 INPUT-BUFFERED SWITCHES

follows:

1.Each unmatched input sends a request to every output for which it has a queued cell.

2.If an unmatched output receives multiple requests, it chooses the one that appears next in a fixed, round-robin schedule starting from the highest-priority element. The output notifies each input whether or not its request was granted.

3.If an input receives multiple grants, it accepts the one that appears

next in a fixed round-robin schedule starting from the highest-priority element. The pointer aj is incremented Žmodulo N . to one location beyond the accepted output. The accept pointers ai are updated only in the first iteration.

4.The grant pointer gi is incremented Žmodulo N . to one location beyond the granted input if and only if the grant is accepted in step 3 of

the first iteration. Like the accept pointers, the pointers gi are updated only in the first iteration.

Because of the round-robin moving of the pointers, we expect the algorithm to provide a fair allocation of bandwidth among all flows. This scheme contains 2 N arbiters, each of which is implementable with low complexity. The throughput offered with this algorithm is 100% for any number of iterations, due to the desynchronization effect Žsee Section 3.3.4.. A matching example of this scheme is shown in Figure 3.9. Considering the example from the iRRM discussion, initially all pointers aj and gi are set to 1. In step 2 of iSLIP, the output accepts the request that is closer to the pointed input in a clockwise direction; however, in a manner different from iRRM, the pointers gi are not updated in this step. They wait for the acceptance result. In step 3,

grant is accepted, the grant pointers change to one position beyond the accepted grant Ži.e., a nonaccepted grant produces no change in a grant pointer position.. The new values for these pointers are g1 s 2, g2 s 1, g3 s 4 and g4 s 1. In the following iterations, only the unmatched input and outputs are considered and the pointers are not modified Ži.e., updating occurs in the first iteration only..

3.3.4 Dual Round-Robin Matching (DRRM)

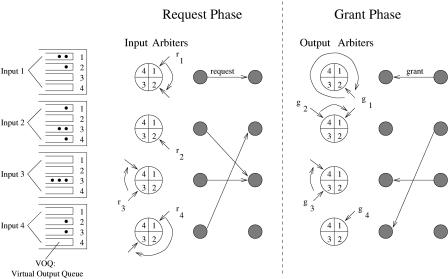
The DRRM scheme w3, 4x works similarly to iSLIP, also using the round-robin selection instead of random selection. But it starts the round-robin selection at inputs. An input arbiter is used to select a nonempty VOQ according to the round-robin service discipline. After the selection, each input sends a request, if necessary, to the destined output arbiter. An output arbiter receives up to N requests. It chooses one of them based on the round-robin

Fig. 3.10 An example of the dual round-robin scheduling algorithm. Ž 2000 IEEE..

service discipline, and sends a grant to the winner input port. Because of the two sets of independent round-robin arbiters, this arbitration scheme is called dual round-robin ŽDRR. arbitration.

The DRR arbitration has four steps in a cycle: Ž1. each input arbiter performs request selection, and Ž2. sends a request to the output arbiters; Ž3. each output arbiter performs grant arbitration, and Ž4. the output arbiters send grant signals to input arbiters. Figure 3.10 shows an example of the DRR arbitration algorithm. In a request phase, each input chooses a VOQ and sends a request to an output arbiter. Assume input 1 has cells destined for both outputs 1 and 2. Since its round-robin pointer, r1, is pointing to 1, input arbiter 1 sends a request to output 1 and updates its pointer to 2. Let us consider output 3 in the grant phase. Since its round-robin pointer, g3 , is pointing to 3, output arbiter 3 grants access to input 3 and updates its pointer to 4. Like iSLIP, DRRM has the desynchronization effect. The input arbiters granted in different time slots have different pointer values, and each of them requests a different output, resulting in desynchronization. However, the DRR scheme requires less time to do arbitration and is easier to implement. This is because less information exchange is needed between input arbiters and output arbiters. In other words, DRRM saves the initial transmission time required to send requests from inputs to outputs in iSLIP.

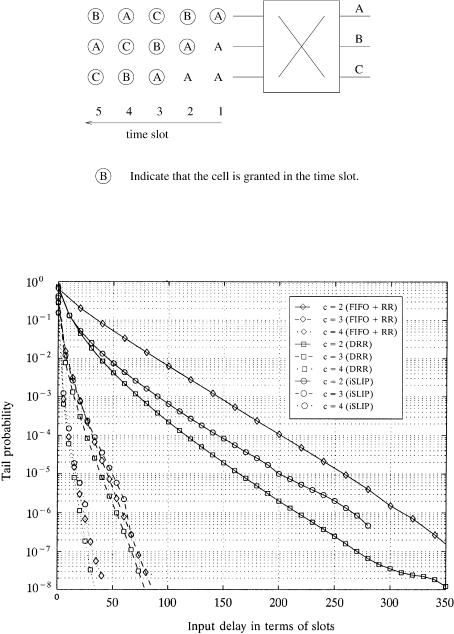
Consider the fully loaded situation in which every VOQ always has cells. Figure 3.11 shows the HOL cells chosen from each input port in different time slots. In time slot 1, each input port chooses a cell destined for output A. Among those three cells, only one Žthe first one in this example. is granted and the other two have to wait at HOL. The round-robin ŽRR. pointer of the

64 INPUT-BUFFERED SWITCHES

Fig. 3.11 The desynchronization effect of DRRM under the fully loaded situation. Only HOL cells at each input are shown for illustration. Ž 2000 IEEE..

Fig. 3.12 Comparison of tail probability of input delay under three arbitration schemes.

first input advances to point to output B in time slot 2, and a cell destined for B is chosen and then granted because of no contenders. The other two inputs have their HOL cells unchanged, both destined for output A. Only one of them Žthe one from the second input. is granted, and the other has to wait until the third time slot. At that time, the round-robin pointers among the three inputs have been desynchronized and point to C, B, and A, respectively. As a result, all three cells chosen are granted.

Figure 3.12 shows the tail probability under FIFO q RR ŽFIFO for input selection and RR for round-robin arbitration., DRR, and iSLIP arbitration schemes. The switch size is 256, and the average burst length is 10 cell slots Žwith the on off model.. DRR’s and iSLIP’s performance are comparable at a speedup of 2, while all three schemes have almost the same performance at speedups c G 3.

3.3.5 Round-Robin Greedy Scheduling

Although iSLIP and DRRM are efficient scheduling algorithms to achieve high switch throughput, they have a timing constraint that the scheduling has to be completed within one cell time slot. That constraint can become a bottleneck when the switch size or a port speed increases. For instance, when considering a 64-byte fixed-length cell at a port speed of 40 Gbitrs ŽOC-786., the computation time available for maximal-sized matching is only 12.8 ns.

To relax the scheduling timing constraint, a pipeline-based scheduling algorithm called round-robin greedy scheduling ŽRRGS. was proposed by Smiljanic´ et al. w30x.

Before we describe pipelined RRGS, nonpipelined RRGS is described. Consider an N N crossbar switch, where each input port i, i g 0, 1, . . . , N y 14, has N logical queues, corresponding to each of the N outputs. All packets are fixed-size cells. The input of the RRGS protocol is the state of all inputroutput queues, or a set C s Ži, j. there is at least one packet at

time slot, an input can only transmit one packet, and an output can receive only one packet. The schedule for the kth time slot is determined as follows:

Step 3: Choose in a round-robin fashion the output j from Ok such that Ži, j. g Ck . If there is none, remove i from Ik and go to step 2.

Step 4: Remove input i from Ik , and output j from Ok . Add Ži, j. to Sk . Go to step 2.