Тема 6. Функции случайных величин и векторов

1)Закон распределения функции случайных величин.

2)Композиция распределений.

3)Распределения: хи-квадрат Пирcона, t-Стьюдента, F-Фишера-Снедекора.

1) Закон распределения функции случайных величин.

Пусть имеется непрерывная случайная величина X с функцией плотности вероятности f(x). Другая случайная величина Y связана со случайной величиной X функциональной зависимостью: Y=φ(X). Случайная точка (X,Y) может находиться только на кривой y=φ(x).

Дифференциальная функция случайной величины Y определяется при условии, что φ(x) - монотонна на интервале (a,b), тогда для функции φ(x) существует обратная функция: φ^-1=Ψ, х = Ψ(y).

Обычно числовая прямая разбивается на n промежутков монотонности и обратная функция находится на каждом из них, поэтому:

, (5.1)

g(y) - дифференциальная функция случайной величиныY.

Математическое ожидание и дисперсию случайной величины Y– функции случайной величиныX(Y=(Х)), имеющей дифференциальную функциюf(x), можно определить по формулам:

(5.2)

. (5.3)

Пример. Случайная величина X подчиняется нормальному закону распределения с математическим ожиданием а и дисперсией ², то есть дифференциальная функция имеет вид:

Найти дифференциальную функцию случайной величины Y=X²

Решение. На (0;) , для y=x², обратная функция x==₁;

на (- ;0) - обратная функция x= -=_{2 .}По формуле (5.1):

g(y)= =

=

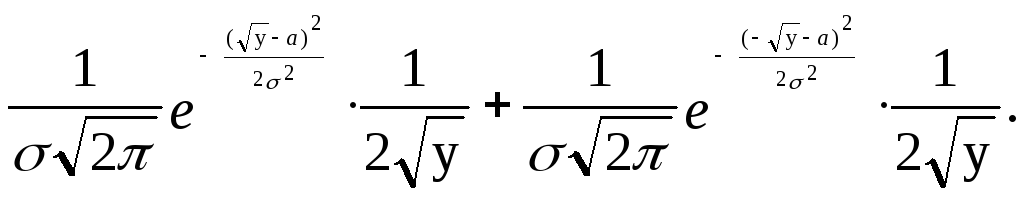
При a=0 и=1:.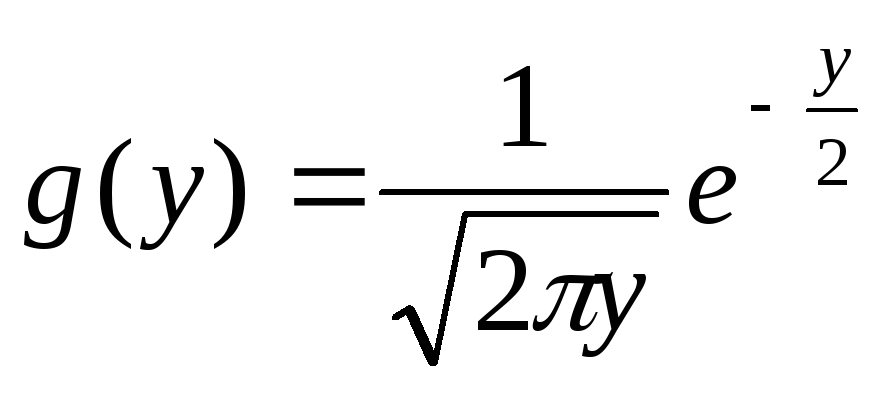

2) Композиция законов распределения

В приложениях часто рассматривается вопрос о распределении суммы нескольких случайных величин. Например, пусть Z=X+Y, тогда G(z) -интегральную функцию случайной величиныZможно определить по формуле:

G(z) =dyf(x, z-x)dx=dxf(z-y,y)dy, (5.4)

где f(x,y)-дифференциальная функция системы случайных величин (X,Y);

область D– полуплоскость, ограниченная сверху прямойy=z-x.

Отсюда, .

Если X и Y независимы, то говорят о композиции законов распределения случайных величин и дифференциальная функция случайной величины Zопределяется как

g(z)=f ₁ (x) f₂(z-x)dx=f ₁ (z-y) f₂(y)dx, (5.5)

где f ₁(x) и f₂(y) дифференциальные функции случайной величины X и Y соответственно.

Если возможные значения аргументов неотрицательны, то дифференциальную функцию случайной величины Zопределяют по формуле:

g(z)=f ₁(x)f₂(z-x)dx(5.6)

или

g(z)=f ₁(z-y)f₂(y)dy. (5.7)

3) Специальные законы распределения

1. ² -распределение Пирсона. ПустьX₁,X₂, …,X_nодинаково распределенные по нормальному закону случайные величины, являющиеся взаимно-независимыми, для которых математическое ожидание равно нулю, а среднеквадратическое отклонение 1, тогда сумма квадратов этих случайных величин носит название случайной величины χ² - xu-квадрат с=n степенями свободы:

(5.8)

При ν=1 (учитывая пример ) дифференциальная функция ²:

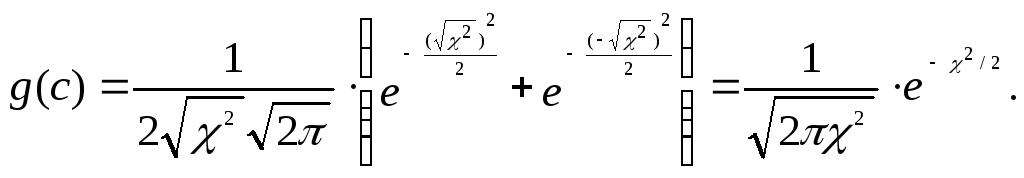
Дифференциальная функция распределения χ²с=n степенями свободы

задаётся формулой

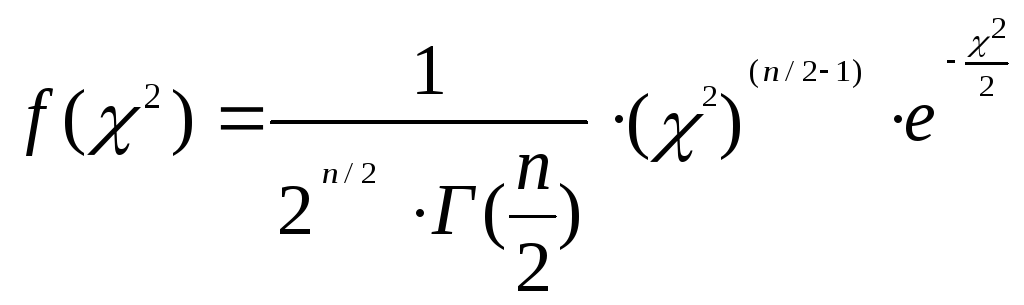, (5.9)

где Г(x) -гамма, функция Эйлера.

Г(x)=, при R₊; еслиnZ, то Г(n+1)=n!

С возрастанием числа степеней свободы = n, распределение χ² медленно приближается к нормальному закону распределения. На практике используют обычно не плотность вероятности, а квантили распределения (прил. 2).

2. t– распределение Стьюдента. Это распределение имеет большое значение при статистических вычислениях, связанных с нормальным законом распределения, где – неизвестный параметр распределения и подлежит определению из опытных данных, например, при статистической обработке наблюдений с неизвестной точностью.

Пусть X,X₁,X₂,…,X_k− независимые нормально распределённые случайные величины с нулевыми математическими ожиданиями и одинаковыми дисперсиями. Безразмерная величинаt:

t = =, (5.10)

называется дробью Стьюдента.

Ее распределение не зависит от в силу ее безразмерности. Дифференциальная функцияt-распределения с=kстепенями свободы имеет вид:

f(t)=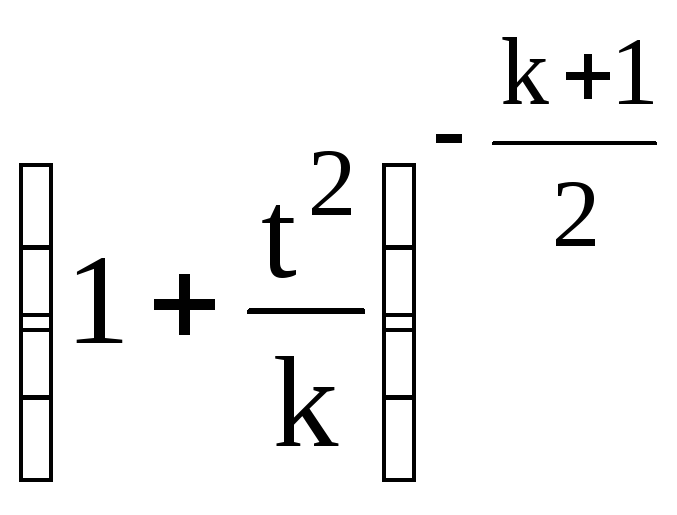. (5.11)

t-распределение Стьюдента, которое быстрее, чем χ² стремится к нормальному.

3. F- распределение Фишера-Снедекора.

Пусть X₁, X₂, …,X_mиY₁,Y₂, …,Y_nодинаково распределенные по нормальному закону случайные величины, являющиеся взаимно-независимыми, для которых математическое ожидание равно нулю, а среднеквадратическое отклонение равно единице.

Рассмотрим дробь Фишера: F(m,n)=, (5.12)

она имеет F - распределение с ₁=m- числом степеней свободы числителя, и₂=n- числом степеней свободы знаменателя ((m, n) степенями свободы), которое называется распределением Фишера-Снедекора.)

Распределения ² - Пирсона, t - Стьюдента, F - Фишера-Снедекора нашли широкое применение в математической статистике, в частности при проверке статистических гипотез и в дисперсионном анализе.