Тема 12. Проверка статистических гипотез

Лекция 1. Вопросы:

1)Понятие и виды статистических гипотез.

2)Статистический критерий проверки гипотез.

3)Уровень значимости. Мощность критерия.

1)Понятие и виды статистических гипотез.

Статистической гипотезой называется всякое высказывание о генеральной совокупности, проверяемое по выборке. Статистические гипотезы делятся на:

Параметрические - это гипотезы, сформулированные относительно параметров (среднего значения, дисперсии и т.д.) распределения известного вида;

Непараметрические - это гипотезы, сформулированные относительно вида распределения (например, определение по выборке степени нормальности генеральной совокупности).

Процесс использования выборки для проверки гипотезы называется статистическим доказательством. Основную выдвигаемую гипотезу называют нулевой H₀. Наряду с нулевой гипотезой рассматривают ей альтернативную H₁. Например, H₀: M(х)=1, математическое ожидание генеральной совокупности равно 1; H₁: M(х)>1, или M(х)<1, или M(х)1 (математическое ожидание больше 1, или меньше 1, или не равно 1).

Выбор между гипотезами H₀ и H₁может сопровождаться ошибками двух родов. Ошибка первого рода α означает вероятность принятия H₁, если верна гипотеза H₀:. Ошибка второго рода означает вероятность принятия H₀, если верна гипотеза H₁:. Существует правильное решение двух видов:и.

Ошибки первого и второго рода

Принятая гипотеза	Н0	Н1
H0 - верна	P(Н0/Н0)=1-	P(Н1/Н0)=
H0 – неверна	P(Н0/Н1)=	P(Н1/Н1)=1-

Правило, по которому принимается решение о том, что верна или не верна гипотеза Н₀, называется критерием, где:

=P(Н₁/Н₀) - уровень значимости критерия;

M=1-=P(Н₁/Н₁) - мощность критерия.

2)Статистический критерий проверки гипотез

Статистическим критерием K называют случайную величину, с помощью которой принимают решение о принятии или отклонении Н₀.

Замечание. Для проверки параметрических гипотез используют критерии значимости, основанные на статистиках: u, χ²,t,F(приложения 5-7). Непараметрические гипотезы проверяют с помощью критериев согласия, использующих статистики распределений:, Колмогорова-Смирнова [1, 2, 6, 10] и т.д.

Например, Н₀: М(х)=10. В зависимости от альтернативной гипотезы рассматривают три случая.

1. Если

Рис 27. Двусторонняя критическая область

В этом случае рассматривают двустороннюю критическую область и используют дифференциальную функцию f (K/H₀), для определения соответствующих квантилей (границ области принятия гипотезы - левой (К_1-/2) и правой (К_/2)). Площадь под криволинейной трапецией дифференциальной функции слева от К_1-/2 и справа от К_/2 равна/2.

Общая площадь ограниченная криволинейной трапецией дифференциальной функции, квантилями и осью абсцисс равна (1 - α) (рис. 27):

(11.1)

2. Если то рассматривается правосторонняя критическая область (площадь под криволинейной трапецией справа от К_равна) (рис. 28):

(11.2)

Рис. Правосторонняя критическая область

3. Если , то рассматривается левосторонняя критическая область (площадь под криволинейной трапецией слева от К_1-равна) (рис. 29):

(11.3)

Рис. Левосторонняя критическая область

Алгоритм проверки статистических гипотез состоит из следующих этапов:

Располагая выборочными данными (), формируют нулевую гипотезуи конкурирующую гипотезу Н_1.

Задают уровень значимости α (обычно принимают α =0,1; 0,01; 0,05; 0,001).

Рассматривается выборочная статистика наблюдений (критерий) К, обычно одна из перечисленных ниже:

u - нормальное распределение;

χ²- распределение Пирсона (хи – квадрат);

t - распределение Стьюдента;

F - распределение Фишера - Снедекора.

4. На основании выборки - определяют значение критерия (статистики) К (приложения 5-7). В зависимости от вида альтернативной гипотезы выбирают по соответствующей таблице квантили критерия для двусторонней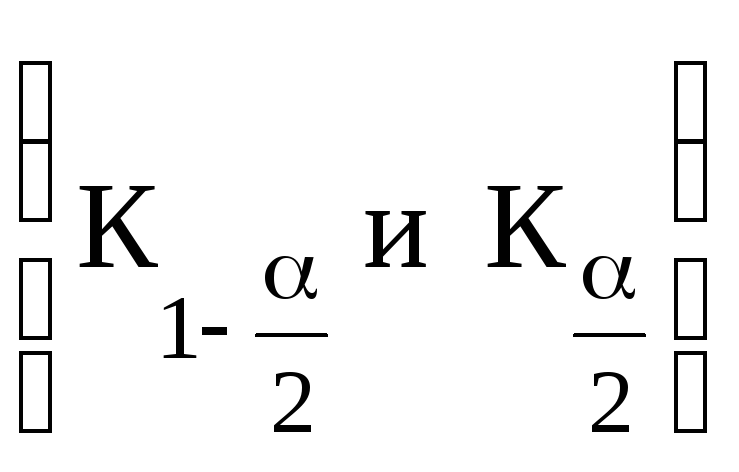или односторонней области (К_1-или К_) (приложения 1-4). Если значения критерия попадают в критическую область, то H₀отвергается; в противном случае принимается гипотеза H₀и считается, что Н₀не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной).

Следует отметить, что возможность принятия гипотезы происходит из принципа невозможности наступления маловероятных событий. Те же события, вероятность которых близка к 1, принимаются за достоверные. Возникает проблема выбора уровня риска (уровня значимости ).

В одних случаях возможно пренебрегать событиями р<0,05, в других нельзя пренебрегать событиями, которые могут появиться с р=0,001 (разрушение сооружений, транспортных средств и т.д.).

Лекция 2.Проверка гипотез о равенстве средних. Критерии согласия.

Пусть требуется проверить нулевую гипотезу о нормальном законе распределения случайной величины. Уровень значимости принять =0,001 .

Обычно точные параметры гипотети­ческого нормального закона нам неизвестны, поэтому нулевую гипо­тезу (Н₀) словесно можно сформулировать следующим образом: F(х) является функцией нормального распределения с параметрами М(X) =а =и D(X) =.

Для проверки этой нулевой гипотезы найдем точечные оценки математического ожи­дания и среднего квадратического отклонения нормально распреде­ленной случайной величины:

: (11.4)

При проверке гипотезы о нормальном распределении генеральной совокупности сравниваются эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормальности распределения) частоты. Для этого используются статистика ²– Пирсона с=k-r-1 степенями свободы (k– число групп,r– число оцениваемых параметров, в настоящем примере оценивались математическое ожидание и среднее квадратическое отклонение, следовательно,r= 2). Если²_расч.²_кр., то нулевая гипотеза отвергается и считается, что предположение о нормальности распределения не согласуется с опытными данными. В противном случае (²_расч.<²_кр.) нулевая гипотеза принимается.

Вычисляются теоретические вероятности р_i, попадания СВ ХN в частичные интервалы [x_i-1; x_i) по формуле:

, (i=1,2,...,k), (11.5)

где

. (11.6)

Применение критерия ², для проверки гипотезы о нормальности распределения предполагает наличие в каждом частичном интервале не менее пяти единиц, в противном случае желательно объединять эти интервалы с соседними.

Проверка гипотезы о принадлежности СВ показательному, биномиальному, пуассоновскому или другому распределению основывается на применении в описанном алгоритме соответствующих интегральных функций.

По таб­лице квантилей ²-распределения , при заданном уровне значимостии числе степеней свободы=k-r-1 находится критическое значение, которое сравнивается с фактически наблюдаемым значением. Если²_расч.<²_{кр. ,}то нет оснований для отклонения нулевой гипотезы о нормальном законе распределе­ния.

Пример. Из нормальной генеральной совокупности сельскохозяйственных предприятий, рассматриваемых по показателю урожайности пшеницы, с известным средним квадратическим отклонением =9,4 и генеральной средней=38,1, извлечена выборка объема n=50. По ней найдена выборочная средняя=42. Требуется при уровне значимости=0,05 проверить нулевую гипотезу Н₀:

а) , при конкурирующей гипотезе Н₁:38,1;

б) , при конкурирующей гипотезе Н₁:<38,1;

в) , при конкурирующей гипотезе Н₁:>38,1.

Решение. Необходимо рассмотреть критерий К=u, где (11.7)

а) По условию конкурирующая гипотеза имеет вид 38,1, поэтому критическая область двусторонняя. Найдем критическую точку из равенства Ф(u_кр.,/2)=(1-)/2=(1-0,05)/2=0,475. Согласно приложения 1: u_кр.=1,96.

, поэтому следует отклонить нулевую гипотезу, то есть выборочная и гипотетическая генеральная средняя статистически различаются значимо.

б) По условию конкурирующая гипотеза имеет вид <38,1, поэтому критическая область левосторонняя. Найдем критическую точку из равенства Ф(u_кр.,)=(1-2)/2=(1-0,1)/2=0,45. Согласно приложения 1: u_кр.= -1,65. u_расч.> u_кр., поэтому следует принять нулевую гипотезу Н₀, то есть выборочная и гипотетическая генеральная средняя статистически различаются не значимо.

в) По условию конкурирующая гипотеза имеет вид >38,1, поэтому критическая область правосторонняя. Найдем критическую точку из равенства Ф(u_кр.,)=(1-2)/2=(1-0,1)/2=0,45. Согласно приложения 1: u_кр.=+1,65. u_расч.> u_кр..поэтому следует отклонить нулевую гипотезу Н₀, то есть выборочная и гипотетическая генеральная средняя статистически различаются значимо.

Пример. Оценить существенность различий в средней урожайности двух сортов озимой пшеницы, если для первого сорта средняя урожайность ц/га и выборочная дисперсия, а для второго сорта средняя урожайностьи выборочная дисперсия. Объемы выборокn₁=5 иn₂=5 соответственно.

Решение. Выдвигаем нулевую гипотезу о том, что средние урожайности двух сортов пшеницы не отличаются друг от друга, т.е. , при альтернативной гипотезе-урожайности существенно различны.

Примем уровень значимости .Так как выборки независимы, причем,то применим критерийt– Стьюдента сстепенями свободы.

. (11.8)

Критическое значение t-распределения:,при числе степеней свободы.

Так как t_расч.>t_кр , то нулевую гипотезу следует отклонить. Следовательно, два сорта пшеницы отличаются статистически значимо по величине урожайности.

Если проверяется нулевая гипотеза о равенстве двух выборочных средних (), при конкурирующей гипотезе( уровень значимости принять равным 0,05), то используется критерийt– Стьюдента сстепенями свободы:

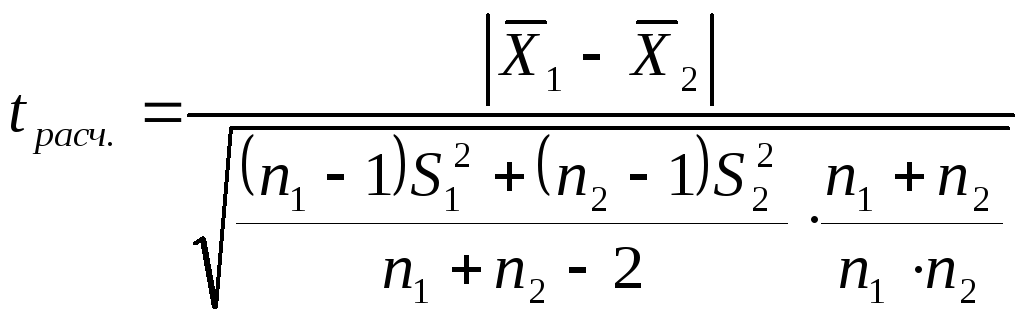. (11.9)

Пример. Два сорта озимой пшеницы испытывались на одинаковом числе участков на протяжении семи лет (табл.8).

При уровне значимости проверить нулевую гипотезу о существенности различий в урожайности двух сортов озимой пшеницы.

Решение. Так как имеются две зависимости выборки, т.е. существует определенная корреляция между урожайностью сортов по годам, то необходимо оценить значимость не разности двух выборочных средних, а средней разности.

Выдвигаем нулевую гипотезу: средняя величина различий в урожайности пшеницы равна нулю,при.

Вспомогательная таблица для расчета ошибки средней разности

Год	Урожайность, ц/га		Разность
	х2i	x1i
1995	46	53	6	1	1
1996	48	43	5	0	0
1997	46	45	-1	-6	36
1998	51	56	5	0	0
1999	52	58	6	1	1
2000	48	55	7	2	4
2001	52	59	7	2	4
Сумма			35	0	40

. По данным таблицы найдем среднюю разность и ошибку средней разности:

; ;,

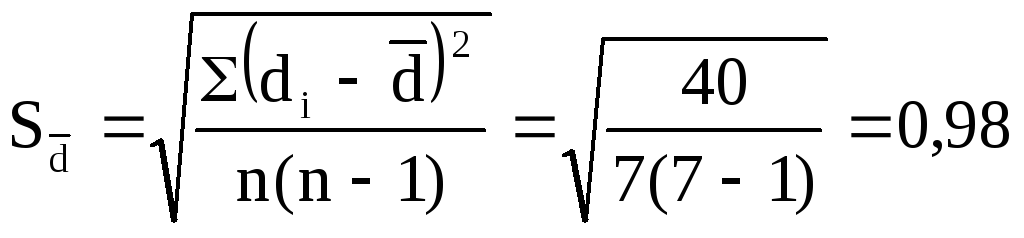где ,n– число пар наблюдений.

При =0,05;k=n-1=7-1=6,t_кр.=2,45

Сопоставив расчётное значение tс критическим, можно сделать вывод, что два сорта существенно различаются по уровню урожайности.