3 Математическое ожидание и его свойства.

На практике нет необходимости характеризовать величину полностью. Обычно достаточно указать только отдельные числовые параметры распределения. Такие числовые параметры принято называть числовыми характеристиками распределения. Прежде всего, это характеристики положения ряда распределения: математическое ожидание, медиана, мода; характеристики рассеяния: дисперсия, среднее квадратическое отклонение.

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие значения приняла другая случайная величина. В противном случае они являются зависимыми.

Математическим ожиданием M(X) дискретной случайной величиныXназывается среднее значение случайной величины:

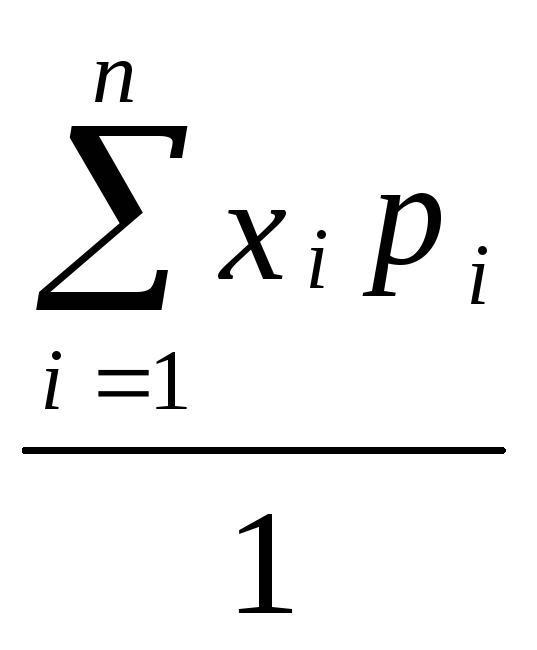===. (2.6)

Или иначе, M(X) - это сумма парных произведений случайной величины на соответствующую вероятность:

=. (2.7)

Мода M_о(X) распределения – это значение случайной величины, имеющее наиболее вероятное значение.

Медиана M_e(X) – это значение случайной величины, которое делит таблицу (закон) распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5.

Свойства математического ожидания:

1) M(C) =C, гдеC=const;

2) M(CX) = CM(X);

3) M(X±Y) = M(X) ± M(Y);

4) Если случайные величины X и Y, независимы, то M(XY) = M(X)M(Y);

5) М (Х – М(Х)) = 0.

Для распределения Бернулли М(Х)=p;

для биномиального распределения: M(X)=np;

для геометрического закона: M(X)=q/p;

для геометрического закона +1: M(X)= 1/р;

для отрицательного биномиального распределения: М(Х)=(кq)/p;

для распределения Пуассона: M(X)=.

4 Дисперсия дискретной случайной величины и ее свойства

Дисперсия служит для характеристики рассеяния случайной величины относительно ее математического ожидания и характеризует форму кривой распределения.

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания:

==. (2.8)

Свойства дисперсии:

1. D(С) = 0, где C=const;

2. D(CX)=C²D(X);

3. D(X)=M(X²)-(M(X))²,

где ;

4. Если случайные величины X и Y независимы, то:

D(XY)= D(X) + D(Y);

5) D(C+X)= D(X);

6) Для любых случайных величин Х и Y, D(XY)=D(X)+D(Y)2cov(X,Y),

где cov(X,Y)=M((X-m_x)(Y-m_y)) - ковариация случайных величин X и Y (М(Х)= m_x, М(Y)= m_y).

Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Дисперсия характеризует средний квадрат отклонения ДСВ, поэтому на практике часто используют в качестве характеристики разброса среднее квадратическое отклонение (X)=, которое имеет ту же размерность, что и СВ Х.

Для распределения Бернулли: D(Х)=pq;

для биноминального закона: D(X)= npq, (Х)=;

для геометрического закона и для геометрического закона+1: D(X)=;

для отрицательного биномиального распределения:D(Х)= (кq)/(p²);

для гипергеометрического: D(X)=;

для распределения Пуассона: D(X)= .

Только для распределения Пуассона M(X)=D(X) =.