
Прикл мех
.pdf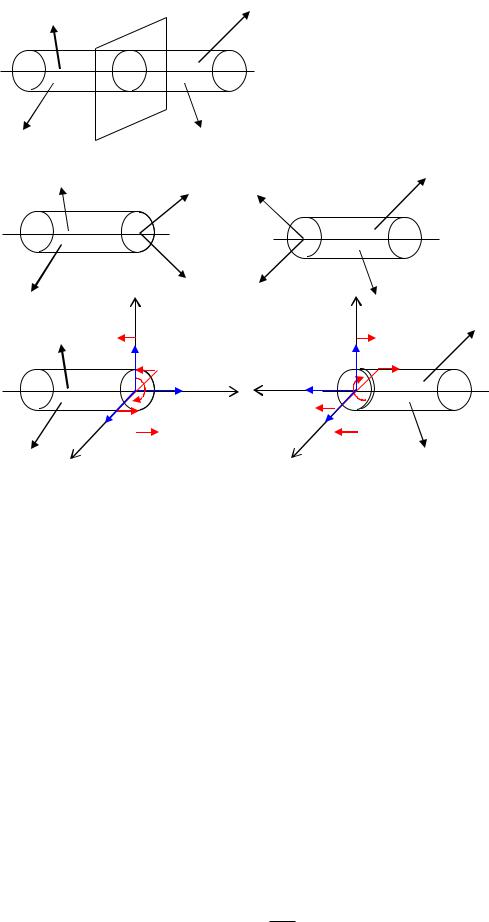
Pn
P1
P2 |
|
|
Pk |
|
||
|
|
|
|
|
||
P1 |
|
|
|
|
Pn |
|
M |
|
|
||||
M |
||||||
|
||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
R |
|
||
P2 |
|
|
|
|
|
|
|
|
Pk |
|
|
y |
|
|
|
|
|
|
|
P1 |
Mz |
|
|
|
|
|
|
Mz |
Pn |
|
Qy |
N |
|
Qy |
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
N Mx |
|
|
|||
|
|
|
|
|
x |
|
|
|
|
|
My |
Mx |
|
|
|
|
My |
|
|
|
|
|
|
|
|
Qz |
|
|
|
|
Qz |
|
|
|
|
|
|
|
|
P2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо відомі зовнішні сили, усі шість компонент внутрішніх сил можуть бути знайдені з |
|||||||||
рівнѐнь рівноваги: |
|
|
|
|
N X 0 |
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
Qy Y 0 |
|
|||
|
|
|
|
|
Qz Z 0 |
|
|||
|
|
|
|
|
M x M xз 0 |
|
|||
|
|
|
|
|
M y |
M yз 0 |
|
||
|
|
|
|
|
M z |
M zз 0 |
|
||
Напруження
Розглѐнемо нескінчено малий елемент площі dF перерізу. Унаслідок малості елементу можна вважати, що внутрішні зусиллѐ, ѐкі діять в його різних точках, однакові за модулем та напрѐмком. Тоді їх рівнодійна dP проходить через центр ваги елемента.
Нормальне напруженнѐ:
dNdA ,
де dN – елементарна повздовжнѐ сили ( проекціѐ dP на ось х).
Дотичні напруженнѐ:

|
|
|
dQy |
|
|
|
dQ |
|
y |
|
z |
z |
, |
||||
dA |
|
|||||||
|
|
|
|
dA |
||||
|
|
|
|
|
|
|||
де dQy, dQy, – елементарні поперечні сили ( проекції dP на осі y,z).
Повне напруженнѐ:
p dFdP 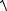
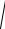 2 y2 z2 .
2 y2 z2 .
Визначеннѐ залежності між зовнішніми силами з одніюї сторони, напруженнѐм, деформаціюя з другої – основна задача опору матеріалів.
Розтяг та стиск
Розтѐг чи стиск часто зустрічаятьсѐ в елементах машин чи споруд (розтѐг торсу крана при підйомі вантажу; шатун двигуна, сприймаю стискуячі навантаженнѐ; штоки циліндрів у підйомо– транспортних машинах).
Розтѐг або стиск – це випадок навантаженнѐ стрижнѐ, що характеризуютьсѐ його подовженнѐм чи укороченнѐм. Розтѐганнѐ чи стисненнѐ спричиняютьсѐ силами Р, що діять вздовж оси стрижнѐ.
При розтѐганні стрижень подовжуютьсѐ, а його поперечні розміри зменшуятьсѐ. Зміну L початкової довжини L стрижнѐ називаять абсолютним подовженням при розтѐзі або абсолютним скороченням при стисканні. Відношеннѐ абсолятного подовженнѐ (скороченнѐ) до початкової довжини стрижнѐ називаютьсѐ відносним подовженням:
L .
L
Уцьому разі:
вісь стрижнѐ залишаютьсѐ прѐмоя лініюя,
поперечні перерізи стрижнѐ зменшуятьсѐ уздовж його осі паралельно самим себе (тому, що поперечний переріз – це площина перпендикулѐрна осі стрижнѐ, а вісь – прѐма лініѐ);
поперечні перерізи залишаятьсѐ плоскими.
Всі волокна стрижнѐ подовжуятьсѐ на одну й ту саму величину L і їхні відносні подовженнѐ однакові:
const .
Різницѐ відповідних поперечних розмірів післѐ деформації і до неї називаютьсѐ поперечною деформацією.
h h1 hb b1 b
Відношеннѐ абсолятної поперечної деформації на відповідний початковий розмір називаютьсѐ
відносною поперечною деформацією:

h b . h b
Між поперечноя та повздовжньоя деформаціѐми існую співвідношеннѐ. Коефіцієнт Пуассона:
.
Коефіціюнт Пуассона безрозмірна величина, що перебуваю в межах 0...0,5 (длѐ сталі 0,3).
В поперечних перерізах виникаять нормальні напруженнѐ . Залежність напружень від деформацій встановляю закон Гука:
E ,
де Е – модуль повздовжньої пружності, модуль пружності першого роду, модуль Юнга, характеризую пружні властивості матеріалу (длѐ сталі Е 2 105 МПа).
В перерізі стрижнѐ виникаю один внутрішній силовий фактор – повздовжня сили N. Повздовжнѐ сила N ю рівнодійноя нормальних напружень ,ѐка чисельно дорівняю алгебраїчній сумі всіх зовнішніх сил, що діять на одну з частин розсіченого стрижнѐ і напрѐмлені вздовж його осі.
Нормальне напруження :
NA .
Враховуячи, що E та L :
L
E L N
L A
L NLEA
EAN .
Добуток EA називаютьсѐ жорсткістю поперечного перерізу стрижня при розтѐганні чи стиску, і маю розмірність сили.
Механічні характеристики матеріалу
До механічних характеристик належать:
модуль пружності Е,
коефіціюнт Пуассона ,
пластичність,
твердість,
міцність.
Длѐ визначеннѐ цих характеристик використовуять випробуваннѐ. Найбільш поширені випробуваннѐ на розтѐг. Длѐ випробувань 
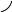 використовуять спеціальні зразки.
використовуять спеціальні зразки. 


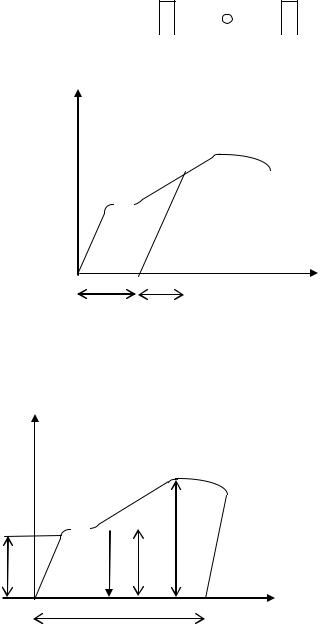
Основноя цілля випробувань ю побудова діаграми розтѐгу стиску, тобто залежність
між силоя, ѐка дію на зразок, та його подовженнѐм. Особливості діаграми розтѐгу мало |
||||||||
вуглецевої сталі. |
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОА –При порівнѐно малих навантаженнѐх |
|
|
|
|
|
|||
матеріал підданий закону Гуку і післѐ припиненнѐ |
|
|
|
|
|
|||
навантаженнѐ ніѐких остаточних деформації немаю. |
|
|
|
|
D |
|||
Цѐ стадіѐ маю назву пружна стадіѐ. |
|
|
|
|
|
|
||
ВС – У подальшому зріст навантаженнѐ стаю |
В |
С |
|
|
||||
повільнішим у невдовзі зовсім припинѐютьсѐ. Явище |
|
|
||||||
|
|
|
|
|||||
А |
|
|
|
|
||||
зростаннѐ |
деформацій |
при |
постійному |
|
|
|
|
|
|
|
|
|
|
||||
навантаженні маю назву плинності. (ВС – площадка |
|
|
|
|
|
|||
плинності). |
|
|
О |
|
f |
|
|
|
|
|
l |
|
|||||
СD – Післѐ закінченнѐ стадії плинності зразок |
lост |
l |
||||||
|
|
|
|
|
|
|
упр |
|
знову починаю опиратисѐ деформаціѐм. Цѐ ділѐнка |
|
|
|
|
|
|||
називаютьсѐ зміцненнѐм. Якщо повторно навантажити |
зразок |
зникаю ділѐнка плинності |
||||||
(fK > OA). |
Зразок набуваю |
здатності |
сприймати без |
остаточних |
деформацій більші |
|||
навантаженнѐ. Явище збільшеннѐ пружних властивостей у результаті попереднього пластичного деформуваннѐ маю назву нагартовка (наклеп).
У точці D настаю ѐкісна зміна характеру деформацій (утворяютьсѐ шийка, ѐка
прогресую ). |
Руйнуваннѐ |
може |
бути |
|
|
|
|
|||||
доведено до кінцѐ навіть при зменшенні |
|
|
|
|
|
|
|
|
|
|||
навантаженнѐ. |
|
|
|
|
|
|
|
|
|
|
|
|
Точка Е – руйнуваннѐ зразка. |
|
|
|
|
|
|
|
|
|
|
||
Щоб |
виникнути вплив розмірів |
|
|
|
|
|
|
|
|
|
||
будуять діаграму = f( ). |
|
|
|
|
|
|
|
|
|
|
|
|
пц – границя пропорційності – |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
уп т |
в |
|||||||
найбільші |
напруженнѐ, |
длѐ |
ѐких |
|
|
|
|
|||||
справедливий закон Гуку (длѐ сталі 200 |
пц |
|
|
|
||||||||
МПа). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
у – границя пружності – найбільші |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
напруженнѐ, до ѐких матеріал не маю |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
остаточних деформацій (длѐ сталі 200 МПа). |
|
|
|
|
|
|
|
|
|
|||
т – границя плинності – напруженнѐ, при ѐких відбуваютьсѐ зріст деформацій без |
||||||||||||
збільшеннѐ навантаженнѐ (длѐ сталі 240 МПа). |
|
|
|
|||||||||
в – границя міцності – напруженнѐ, ѐкі може витримати зразок без руйнуваннѐ(длѐ |
||||||||||||
сталі 400 МПа). |
|
|
|
|
|
|
|
|
|
|
|
|
Також визначаятьсѐ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
відносне остаточне подовженнѐ післѐ пориваннѐ: |
|
|
|
||||||||

lk l0 100% l0
відносне остаточне звуженнѐ перерізу зразка у місці руйнуваннѐ:
A0 Ak 100%
A0
Взалежності від матеріали поділѐятьсѐ на:
пластичні > 5% (вуглецева сталь, мідь, аляміній),
крихкі < 5% (чавун, бетон, інструментальна сталь).
Діаграма розтѐгу не маю площадки плинності. Длѐ крихких матеріалів проводѐть випробуваннѐ на стисканнѐ, тому що вони краще чинѐть опір стискання ніж розтѐгу (Длѐ пластичних матеріалів модуль пружності, границѐ пружності, границѐ плинності при стисканні приблизно однакові).
Крім крихких та пластичних матеріалів ю ще пружно-в’ѐзні матеріали (поліаміди). Длѐ них характерне ѐвище повзучості і релаксації напружень.
Повзучість – це безперервне зростаннѐ пластичних деформацій при незмінному навантаженні.
Релаксація напружень – повільне зменшеннѐ напружень при незмінній повній деформації за рахунок збільшеннѐ пластичної складової і зменшеннѐ пружності.
Допустимі напруження
Длѐ пластичних матеріалів:
b
n
Длѐ крихких матеріалів:
nm ,
де n –коефіціюнт запасу міцності.
Умова міцності при розтязі:
FA .
Длѐ сталі 3 160 МПа.
Твердість матеріалів
Длѐ визначеннѐ твердості існую три метода: Бринелѐ – твердість визначаютьсѐ ѐк
HB FA ,
де F – сила, з ѐкоя вдавляютьсѐ заготовлена кулька в матеріал,
А– площа від початку.
2.Роквела – використовуютьсѐ алмазний конус і заготовлена кулька, Твердість визначаютьсѐ по різниці на шкалі прибору від дії попереднього навантаженнѐ та повного навантаженнѐ (HRC – конус, HRВ – кулька)

3. Віленса –Длѐ визначеннѐ твердості використовуютьсѐ алмазна пірамід і визначаютьсѐ
HV FA .
Епюри повздовжніх сил та напружень.
Графіки, що показуять, ѐк зміняятьсѐ внутрішню зусиллѐ при переході від перерізу до перерізу, називаютьсѐ епюрами.
Правила побудови епяр:
1.Вісь, на ѐкий будуютьсѐ епяра (база), паралельна осі стрижнѐ.
2.Ордината епяри відкладаютьсѐ від осі епяри по перпендикулѐру.
3.Штрихуять епяри лініѐми, ѐкі перпендикулѐрні до бази.
4.Длѐ зусиль вибираять певний масштаб, проставлѐять значеннѐ характерних ординат, в полі епяри ставлѐть знак зусиллѐ.

Розглѐнемо приклад: Длѐ сталевого стрижнѐ виѐвити закон зміни повздовжніх сил, напружень та переміщень, ѐкщо Е =2 105МПа. Домовимось вважати повздовжня сила додатноя, ѐкщо вона викликаю розтѐг.
1. Стрижень маю дві ділѐнки різної жорсткості. З умови рівноваги будь-ѐкої розсіченої частини стрижнѐ на першій ділѐнці:
0 x1 l1
0 x1 2 м
N1 F 1 2 кН,
на другій ділѐнці:
0 x1 l2
0 x1 1м
N2 F 1 F 5 2 7 5кН.
У обраному масштабі будуюмо епяру повздовжніх сил. 2. Визначаюмо напруженнѐ у перерізах
1 N1 2 103 10 МПа
A1 0,0002
|
|
|
N |
2 |
|
5 |
103 |
|
|
|
|
|
|
|
|
50 МПа |
|
2 |
|
|
|
|
||||
|
|
A2 |
|
0, |
0001 |
|||
|
|
|
|
|||||
У обраному масштабі будуюмо епяру напружень.
3. Визначимо на ѐку величину переміщуютьсѐ кожний переріз стрижнѐ
|
u xn u xn 1 |
|
Nn xn |
|
|
|||||||||||||
|
|
E An |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
на першій ділѐнці: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x1 l1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 x1 2 м |
|
|
||||||||||
|
|
|
u x1 u x0 |
|
|
|
N1 x1 |
|
|
|
||||||||
|
|
|
|
E A |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
u x1 |
|
|
0 |
|
|
2000 x1 |
|
|
||||||||||
|
x1 1 |
|
|
|
|
5 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
10 |
|
0,0002 |
|||||||
u x1 |
|
|
|
0 |
|
|
2000 2 |
0,0001м |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x1 |
|
1011 |
0,0002 |
||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
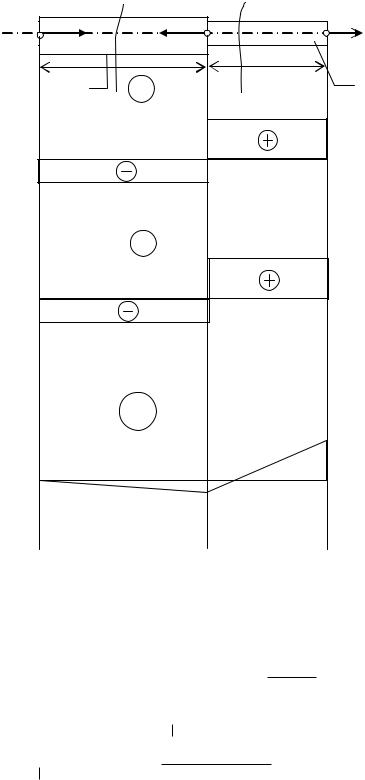
F1=2кH |
|
F2=7кH |
|
|
|
F3=5кH |
|
|
|
|
|
|
|
|
|
|
|
||
|
2 м |
|
|
|
1 м |
|
|
|
|
А2=0,0002м |
N, кН |
|
|
|
|
А1=0,0001м2 |
|
||
2 |
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
2 |
|
|
|
|
|
|
|
|
, |
МПа |
50 |
|
|
50 |
|
|
|
10 |
|
10 |
|
|
|
|
|
|
|
|
и, |
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,00015 |
|
|
|
|
0,0001 |
|
|
|
|
|
|
|
|
на другій ділѐнці: |
|
|
|
|
|
|
|
|
|
|
|
0 x2 |
|
l2 |
|
|
|
||
|
|
0 x2 1м |
|
|
|
||||
|
u x2 u x1 |
|
N2 x2 |
|
|
|
|||
|
E A |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
u x2 x2 0 0,0001 0 0,0001м |
|
|
||||||
u x1 x2 2 0,0001 |
5000 1 |
|
0,00025 |
0,0001 |
0,00015 |
м. |
|||
11 |
|
|
|
||||||
|
|
2 10 |
0,0001 |
|
|
|
|||
Будуюмо епяру переміщень.
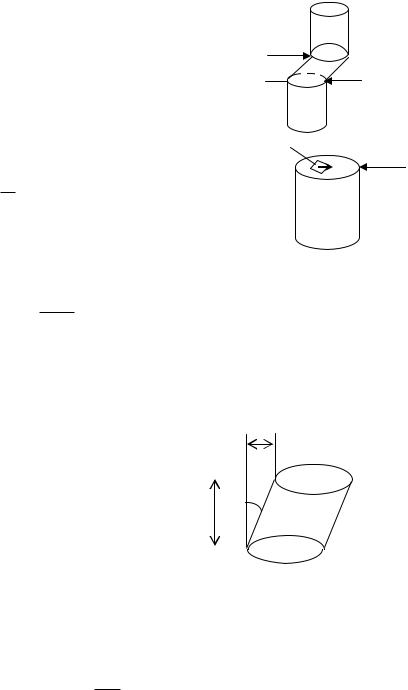
Зсув
Зсув – такий вид навантаженнѐ, при ѐкому один переріз стрижнѐ зміщаютьсѐ відносно другого, а відстань між ними не зміняютьсѐ.
Зсув може бути викликаний діюя двох рівних, паралельних та протилежно напрѐмлених сил, розташованих на близькій відстані одна від одної перпендикулѐрно до осі стрижнѐ.
Деталі, ѐкі служать длѐ з’юднаннѐ елементів металоконструкцій, механізмів та машин – заклепки, болти, шпильки, зварні шви тощо, сприймаять навантаженнѐ, перпендикулѐрні до їх повздовжньої осі, тобто зазнаять зсув.
У внутрішньому перерізі при зсуві виникаю один силовий фактор – перерізуяча сила Q. Дотичні напруженнѐ лежать у площині перерізу. У випадку недостатньої міцності відбуваютьсѐ перерізуваннѐ деталей. Кажуть, що деталі працяять на зріз, і дотичні напруженнѐ називаять напруженнѐми зрізу.
QA
Умова міцності при зсуві:
Qmax ,
A
де * ] – допустимі дотичні напруженнѐ * ] = 0,6 [ ].
F
h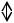
|
|
F |
dA |
|
F |
|
При зсуві одна площина зміщуютьсѐ відносно іншої. Ступень зміщеннѐ характеризуютьсѐ абсолятним зсувом S, ѐкий залежить від відстані h між перерізами. Щоб
виникнути впливу h, вводѐть понѐттѐ відносного зсуву: |
S |
tg S . |
|
|
|
|
|
|
|
||
h |
|
|
||
h |
||||
|
||||
Відносний зсув дорівняю кутовому переміщення |
|
|
|
|
повздовжнього волокна елементу – куту зсуву. |
|
|
|
|
|
|
|
||
Між кутом зсуву та дотичним напруженнѐ існую прѐма |
|
|
|
|
пропорційність – закон Гуку при зсуві: |
|
|
|
|
G ,
де G – пружна постійна матеріалу, модуль зсуву (модуль Юнга другого роду). Величина абсолятного зсуву:
S GAQh ,
де GA – жорсткість при зсуві.
Між модулем повздовжньої пружності Е та модулем зсуву G ю залежність :
G |
E |
|
|
. |
|
2 1 |
||
Длѐ сталі = 0,25, G = 0,4Е, тобто опір зсуву слабкіше ніж опір розтѐгу.
Геометричні характеристики перерізів
1. Площа поперечного перерізу (при розтѐзі, стиску).
A dA .
A
2. Статичні моменти перерізу відносно осей Х та Y (*м3]):
Sx ydA
A
Sy xdA
A
Якщо осі координат проходѐть через центр ваги перерізу статичні моменти дорівняять нуля. Осі називаятьсѐ центральними.
3. Координати центра ваги :
|
|
|
xdA |
|
Sy |
||
x |
|
|
A |
|
|
||
|
|
|
|
||||
|
|
|
|
||||
c |
|
|
A |
|
|
A |
|
|
|
|
|
|
|||
|
|
|
ydA |
|
|
Sx |
|
y |
|
A |
|
||||
|
|
||||||
c |
|
|
A |
|
|
A |
|
|
|
|
|
|
|||
4. Моменти інерції *м4]:
осьові:
Ix y2dA
A
I y x2dA
A
відцентровий
Ixy xydA
A
полѐрний
I 2dA
A
I Ix I y
Осі, відносно ѐких відцентровий момент інерції дорівняю нуля, називаятьсѐ головними осями інерції. Осьові моменти інерції відносно головних осей координат приймаять екстремальні значеннѐ:
|
I |
d 4 |
|
||
|
32 |
|
|||
|
|
|
|||
Ix |
I y |
|
d 4 |
. |
|
64 |
|||||
|
|
|
|
||
Кручення
Крученнѐ маю місце при навантаженні вала зовнішніми силами, площини дії ѐких перпендикулѐрні до його повздовжньої осі (вал зі шківами, зубчастими колесами тощо).
Моменти цих сил – скручуячі моменти.
