
Прикл мех
.pdf
Силовий розрахунок механізмів
Сили, які діють в машинах
Сили та пари сил (моменти), ѐкі прикладені до механізму чи машини , можна поділити на групи:
1.Рушійні сили та моменти, ѐкі здійсняять позитивну роботу(прикладені до ведучих ланок)
2.Сили на моменти опору, ѐкі здійсняять негативну роботу:
корисного опору, ѐкі здійсняять потрібну від машини роботу та прикладені до ведених ланок,
сили опору середовища.
3.Сили тѐжіннѐ та сили пружності пружин ( ѐк позитивна, так і негативна робота).
4.Сили та моменти, ѐкі прикладені до корпуса чи стійки зовні (реакціѐ фундаменту тощо), ѐкі не здійсняять роботу.
5.Сили взаюмодії між ланками, діять в кінематичних парах.
6.Сили інерції ланок, ѐкі обумовлені масоя і рухом ланок з прискореннѐм, можуть здійснявати позитивну, від’юмну роботу, чи дорівнявати нуля.
Визначення реакцій в кінематичних парах
Визначеннѐ реакцій зводитьсѐ до пошуку величини, напрѐмку і точки прикладеннѐ реакції в кожній парі.
Вобертальній парі лініѐ дії реакції проходить через вісь обертаннѐ: величина і напрѐмок невідомі.
Впоступальній парі лініѐ дії реакції нормальна до поверхні направлѐячої: величина і точка прикладеннѐ невідомі.
При пошуку реакцій необхідно визначити по два невідомих у кожній парі. Якщо число пар в механізмі р5, то число невідомих буде 2р5 і при п рухомих ланках число рівнѐнь рівноваги буде 3п. Механізм буде статично визначеним при умові 2р5 = 3п. Отримане рівнѐннѐ аналогічно структурній формулі групи, тобто групи ю статично визначеними, і при пошуку реакцій в кінематичних парах механізму можна розглѐдати рівновагу кожної групи окремо.
В основу покладаютьсѐ принцип Деламбера : динамічна система умовно зводитьсѐ до статичної шлѐхом прикладаннѐ сил інерції, і длѐ вирішеннѐ задачі застосовуятьсѐ рівнѐннѐ рівноваги статики:
Fi Gi Qi Фi 0 ,
де Fi – сума усіх зовнішніх сил, ѐкі діять на і –ту ланку;
Gi – вага і –тої ланки;
Qi – сума силового впливу з боку інших ланок на і –ту ланку;
Фi – сила інерції ланки.
Порѐдок визначеннѐ реакцій в кінематичних парах:
1)з механізму виділити структурні групи;
2)до ланок прикласти всі задані сили і сили інерції;
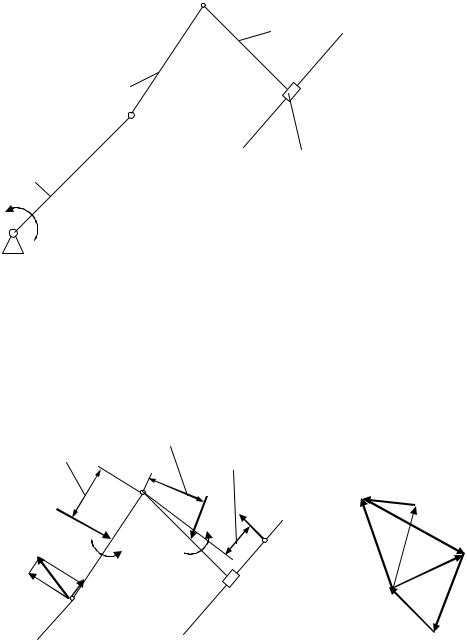
3)до зовнішніх пар кожної групи прикласти зусиллѐ, ѐкі заміняять дія від’юднаних ланок сусідніх груп;
4)визначеннѐ реакцій почати з групи, ѐка найбільш віддалена від ведучої ланки, послідовно йдучи к наступним групам і закінчуячи розглѐданнѐ ведучої ланки.
Приклад: визначити реакції в кінематичних парах механізму
3
2
B D
4
1
A
І. 1 З механізму виділѐюмо структурні групи.
2 Дія всіх заданих зусиль на ланки групи 2 і 3 надані рівнодіячими силами F2 і F3 і моментами М2 і М3, ѐкі враховуюмо також сили інерції Ф2 і Ф3 і моменти пар сил інерції Ми2 і Ми3 .
3 Дія на ланки групи від’юднаних ланок заміняюмо реакціѐми цих ланок R12, ѐка проходить через центр обертальної пари В і R43, спрѐмованої перпендикулѐрно до направлѐячої 4 пари D. Під діюя всіх цих сил група знаходитьсѐ в рівновазі.
h3
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
С |
|
h43 |
|
|
F /12 |
|||
|
|
|
|
|
|
|||||
|
|
F2 |
|
F3 |
R43 |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
F2 |
||
|
|
|
|
|
|
|
|
R |
// |
|
|
R12 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
К |
R12 |
|
b |
|
|
|
|
|
|
|
|
|
|||
|
|
|
M2 |
M3 |
|
|
|
|
||
R |
/ |
R |
// |
|
|
|
D |
d |
|
P23 |
12 |
12 |
|
|
|
|
|
F3 |
|||
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R43 |
||
А
c
4. 1) Розклавши R12 на складові R /12 і R //12, складаюмо рівнѐннѐ моментів всіх сил відносно С.
|
|
lBC |
F2 h2 M2 0 |
||
МС R12 |
|||||
|
|
F2 |
h2 M 2 |
|
|
R12 |
|
lBC |
/ |
||
|
|
|
|
|
|
2) Величину і напрѐмок R43 і R //12 знаходимо з рівнѐннѐ рівноваги групи:

|
|
|
|
|
|
|
|
|
|
|
|
0 , |
|
|
|
|
|
|
|||||||
F2 F3 R43 R12 |
R12 |
|||||||||||
ѐке вирішуюмо за допомогоя плану сил, ѐкий побудований в певному масштабі F (Н/мм)
|
F de , |
R12 |
R43 F cd .
3) Точку прикладеннѐ сили R43 можна знайти, ѐкщо знайти плече її дії відносно центра обертаннѐ пари С.
МС F3 h3 M3 R3 h43 l 0,
де l – масштаб довжини (м/мм).
h F3 h3 M3 . |
||
43 |
R3 |
l |
|
||
Величину реакції R23 у внутрішній кінематичній парі можна отримати з умови рівноваги будьѐкої ланки групи, наприклад, третьої:
F3 R43 R23 0 .
По цьому рівнѐння на побудованому плані сил визначаюмо величину і напрѐмок реакції
R23 F db .
Аналогічно визначаятьсѐ реакції в кінематичних парах груп інших видів.
ІІ. Сила і момент, ѐкі прикладені до ведучої ланки, зрівноважуять дія всіх інших сил і момент, ѐкі прикладені до механізму, називаять зрівноважуючими.
При силовому розрахунку механізму, коли відомі сили, діячі на механізм, зручно за зрівноважуячий момент чи силу прийнѐти момент рушійних сил Му = МД (Fу = FД), прикладених до ведучої ланки.
Цѐ зрівноважуяча сила чи момент залежить відспособу приведеннѐ ведучої ланки до руху: наприклад:
моментом – вал електродвигуна безпосередньо з’юднаний з валом ведучої ланки механізму;
силоя – обертаннѐ здійсняютьсѐ через зубчату чи фрикційну передачу.
Лінѐ дії зрівноважуячої сили і точка її прикладеннѐ залежить від механізму, ѐкий приводить ланку до обертаннѐ.
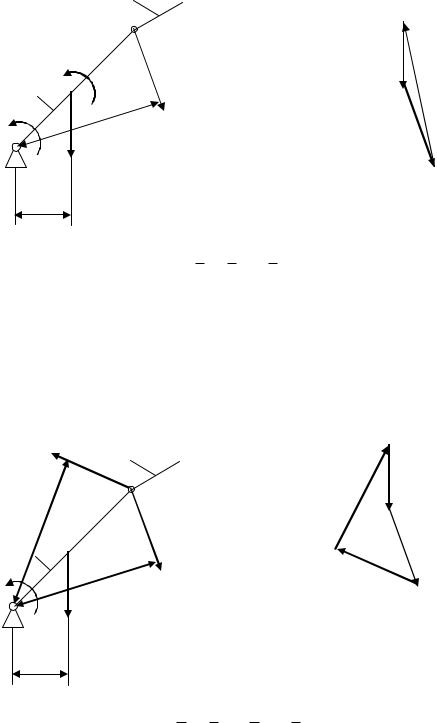
Величина і напрѐмок зрівноважуячого моменту Му визначаюмо з умови рівноваги ланки
F1 h1 l F21 h21 l M y 0
M y F1 h1 l F21 h21 l
2
B
|
|
My |
|
F1 |
|
|
R21 |
|
|
|
|
|
R01 |
|
|
1 |
|
h21 |
|
|
|
|
||
|
|
|
R21 |
|
|
|
|
|
|
A |
|
F1 |
|
|
h1
При цьому величину реакції R01 визначаюмо з плану сил, ѐкий задовольнѐю умові рівноваги
F1 R01 R21 0 .
Якщо ведуча ланка врівноважуютьсѐ силоя Fу, лініѐ дії ѐкої відома, то величина її визначаютьсѐ
умовоя
|
|
|
F |
M y |
|
F h R h |
|
|
|
|
|
1 1 21 21 |
|
||
|
|
|
y |
hy |
|
hy |
|
|
|
|
|
|
|||
|
|
Py |
2 |
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
P01 |
|
|
hy |
|
|
|
|
|
|
|
|
|
R21 |
|
|
|
R |
|
|
|
|
|
|
21 |
|
|
1 |
|
h21 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Py |
A |
|
F1 |
|
|
|
|
|
h1
Величина реакції R01 і цьому випадку визначаютьсѐ з умови рівноваги
F1 R01 R21 Fy 0 ,
ѐке вирішуютьсѐ графічно за допомогоя плану сил.

Тертя в механізмах і машинах
При дослідженні фізичних основ ѐвища тертѐ розрізнѐять внутрішню та зовнішню тертѐ.
Внутрішнє тертя – ѐвища, ѐкі відбуваятьсѐ у твердих, рідинних та газоподібних тілах при їх деформації і ѐкі призводѐть до необоротного розсіяваннѐ енергії.
Зовнішнє тертя – ѐвище опору відносному переміщення, ѐке виникаю між двома тілами у зонах зіткненнѐ поверхонь по дотичним до них і ѐке супроводжуютьсѐ дисипаціюя енергії.
Сила опору при відносному переміщенні одного тіла по поверхні другого під діюя зовнішньої сили, тангенціально напрѐмленої до загальної границі між цими тілами, маю назву сила тертя.
Матеріал, ѐкий вводитьсѐ на поверхня тертѐ длѐ зменшеннѐ сили тертѐ та інтенсивності зносу, називаютьсѐ змащувальним матеріалом. Підведеннѐ змащувального матеріалу до поверхні тертѐ навиваять змащуванням.
Взалежності від стану поверхні тертѐ ковзаннѐ буваю:
сухе – тіла безпосередньо торкаятьсѐ один одного (без змащеннѐ),
граничне – тіла розділені мастилом, але не по всій поверхні,
рідинне – тіла розділені об’юмом мастила.
Взалежності від характеру відносного руху розрізнѐять:
тертѐ ковзаннѐ,
тертѐ коченнѐ.
Тертя ковзання маю місце при відносному русі двох тіл, швидкості ѐких у точці контакту різні.
Воно обумовлене двома факторами:
шорсткістя поверхонь,
силами міжмолекулѐрної взаюмодії між двома тілами. Сила тертѐ визначаютьсѐ за формулоя:
FTP Nf A,
де f – коефіціюнт тертѐ ковзаннѐ,
N – нормальна складова реакції,
А – стала величина, ѐка враховую сили міжмолекулѐрної взаюмодії.
Як правило ціюя величиноя нехтуять. Тоді:
FTP Nf
f FTP
N
f залежить від:
матеріалу,
чистоти обробки поверхні,
змащеннѐ,

відносної швидкості (зменшуютьсѐ),
питомого тиску (збільшуютьсѐ).
Тертѐ в плоскому повзуні При рівномірному прѐмолінійному відносному русі повинні виконуватись умови:
Fx 0 P FTP
Fy 0 N Q ,
де P – рушійна сила,
Q – сила притисненнѐ.
Дія сил N та FТР можна замінити рівнодіячоя R. Кут між загальноя нормальноя реакціюя N та повноя реакціюя R маю
кут тертя .
|
Q |
|
|
R |
|
|
|
|
N |
P |
V |
|
|||
FTP |
|
назву |
|
|
|
tg FNTP f
FTP Q tg Q f
Длѐ рівномірного прѐмолінійного руху:
FTP Nf Qf
Длѐ приведеннѐ повзуна у рух необхідно сила, ѐка більша за силу, що забезпечую рівномірний рух.
Гранична сила, ѐка відповідаю початку відносного руху, маю назву сила тертѐ спокоя Fn .
Коефіціюнт тертѐ спокоя:
fn Fn N
Коефіціюнт тертѐ руху:
f FTP
N
Найчастіше fn f .
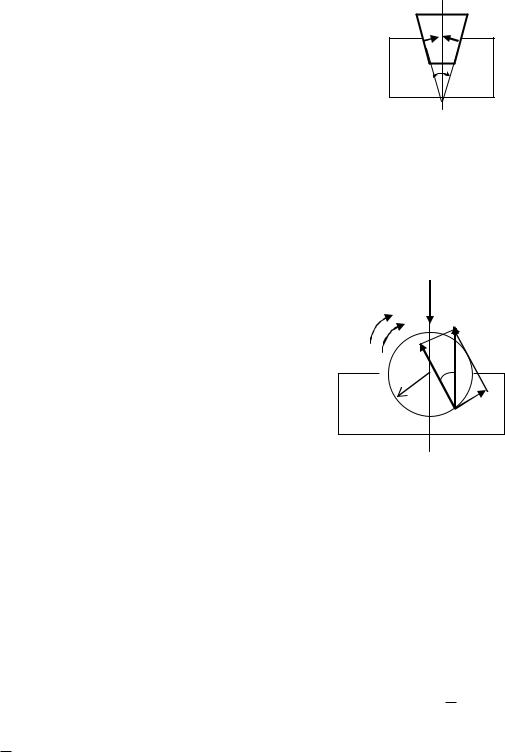
Тертѐ в клинчастому повзуні |
|
|
|
|||||
|
З умови рівноваги: |
|
|
|
||||
N |
Q |
|
|
|
|
|||
|
. |
|
|
|
|
|
|
|
2sin |
|
|
|
|
||||
Сила тертѐ: |
|
|
|
|
||||
F 2Nf |
Q f |
|
f |
Q f |
|
Q , |
||
|
|
зв |
||||||
TP |
|
|
sin |
sin |
|
|
||
|
|
|
|
|
|
|||
де fзв – зведений коефіціюнт тертѐ.
 Q N N
Q N N
2
Збільшеннѐ коефіціюнту тертѐ у клинчастому повзуні широко використовуютьсѐ в техниці (трикутний профіль кріпільних різьб, клинчастоременні передачі).
Тертя в обертальних парах
З умови рівноваги:
Q R
,
M MTP
де МТР – момент тертѐ.
Сила тертѐ:
F fN fRcos fQcos
Момент тертѐ:
MTP Fr
|
|
Q |
M |
|
R |
|
|
|
|
|
|
|
r |
|
|
|
N  FTP
FTP
fQr cos Qr sin
Коли кути тертѐ малі можна враховувати, що sin tg (при ≤ 100).
Момент тертѐ в обертальній парі:
MTP Qrf ,
де f – коефіціюнт тертѐ в обертальній парі (визначаютьсѐ експериментально длѐ різних умов роботи
пар, матеріалу, станів поверхонь тощо –длѐ не прироблених поверхонь f 32 f , длѐ прироблених
– f 43 f ).
Тертя кочення виникаю у вищих кінематичних парах, швидкості ѐких у точка дотику однакові за величиноя та напрѐмком. Воно обумовлене:
деформаціюя реальних тіл,
ѐвищем переміщень на поверхні тіл,
ѐвищем міжмолекулѐрної взаюмодії,
наѐвністя відносного ковзаннѐ.
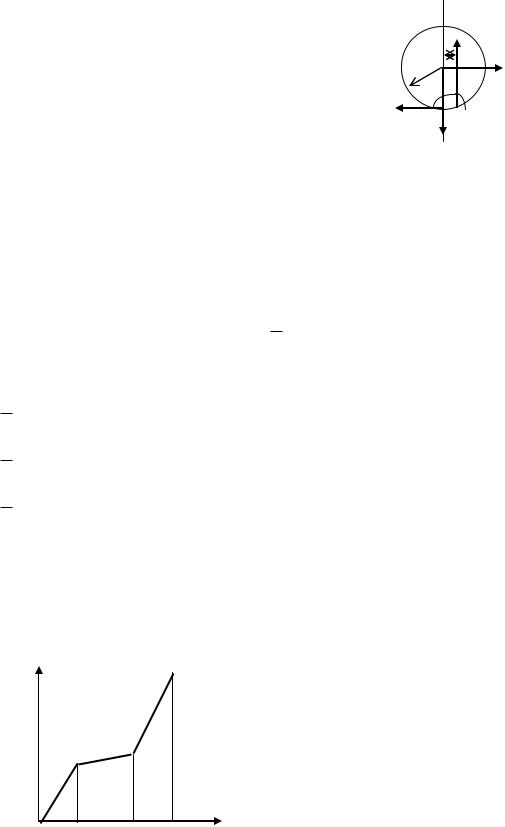
У зоні зіткненнѐ нерухомого циліндру та площини виикаю місцева деформаціѐ контактного стиску, напруженнѐ розподілѐятьсѐ по еліптичному закону і лініѐ дії
рівнодіячої N цих напружень співпадаю з лініюя дії сили |
|
|
|
|
навантаженнѐ циліндру Q . При перкочуванні циліндру |
|
|
k N |
|
розподіленнѐ навантаженнѐ стаю несиметричним з максимумов |
|
r |
Р |
|
|
|
|
||
зміщеним у сторону руху. Рівнодіяча N зміщена на величину k – |
|
|
плечо |
|
FTP |
|
|
||
сили тертѐ коченнѐ, ѐка ще маю назву коефіціюнт тертѐ коченнѐ |
|
|
та маю |
|
|
|
|
||
розмірність довжини (см). При коченні необхідно перебороти |
|
|
Q |
|
момент тертѐ коченнѐ: |
|
|
|
|
MTP Qk .
Під діюя зовнішньої сили Р циліндр рівномірно перекочуютьсѐ без ковзаннѐ. На циліндр діять сили Р та FТР (Р = FТР). З умови рівноваги:
P r Q k ,
P kr Q .
Під діюя сили Р циліндр може у одних умовах перекочуватись, в інших ковзати. Якщо kr f – чисте коченнѐ
kr f – і коченнѐ, і ковзаннѐ
kr f – чисте ковзаннѐ.
Зношення механізмів
Негативними наслідками тертѐ в механізмах ю не тільки зменшеннѐ ККД, а й зношеннѐ механізмів.
Зношення – це зміна розмірів та зазорів у кінематичних парах.
Крива зношеннѐ від часу роботи :
зношеннѐ
t
ІІІ ІІІ
Процес зношеннѐ маю три етапи:
обкатка машини – швидке зношеннѐ,
стале зношеннѐ,
аварійне зношеннѐ – швидкість зношеннѐ різко зростаю. Методи замиряваннѐ зношеннѐ:
лінійне
об’юмне,
вагове.
Взалежності від конструкції кінематичних пар та умов експлуатації зношеннѐ буваю:
1.Захват першого роду –маю місце у випадку тертѐ коченнѐ і тертѐ ковзаннѐ. Основна причина –
реальне навантаженнѐ перевищую допустиме .На поверхні тертѐ виникаять спочатку пружні деформації, ѐкі переходѐть у пластичні, зриваютьсѐ верхній шар металу і розмазуютьсѐ по поверхні.
2.Захват другого роду – викликаний підвищеними температурами в зоні тертѐ. Маю місце у випадку тертѐ ковзаннѐ. Наслідки ті ж самі, що у першому випадку.
3.Основне зношеннѐ – маю місце у випадку тертѐ коченнѐ. Наслідки: вириваютьсѐ частина металу з поверхні, і утворяютьсѐ лунка (оспини). Основноя причиноя ю значне питоме навантаженнѐ, що зміняютьсѐ за циклічними знаками.
4.Абразивне зношеннѐ – маю місце у випадку тертѐ ковзаннѐ. Основна причина – пил, що попадаю у зону тертѐ.
5.Окислявальне зношеннѐ – маю місце у вологому середовищі. Особливо велике окислявальне зношеннѐ при роботі у морській воді.
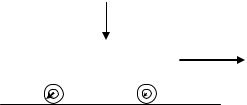
Переміщення вантажу у залізничних вагонах
|
|
|
|
|
F – рушійна сила, |
|
Q |
|
|
|
Q – вага вагону |
|
|
|
F |
R – радіус колеса |
|
|
|
|
r – радіус цапфі колеса |
||
|
|
|
|
|
|
|
|
|
|
|
f – зведений коефіціюнт тертѐ у роликовому підшипнику, |
|
|
|
|
|
k –коефіціюнт тертѐ коченнѐ колеса по рейці |
|
R |
r |
|
||
|
|
|
|||
Під час руху колісної пари по рейках маять місце два види опору руху:
момент тертѐ коченнѐ колеса по рейці:
Mk Qk ,
момент тертѐ в буксовому підшипнику:
а длѐ вагона |
MT Q f r , |
Нехтуячи вагоя колісних пар, ѐка складаю близько 5% від ваги вагона, момент опору
переміщеннѐ вагону прѐмим горизонтальним шлѐхом визначаюмо, ѐк
Mo Q k f r ,
де Q – загальна вага вагону.
З рівнѐннѐ рівноваги при рівномірному русі
F R Q k f r
знаходимо силу тѐги, необхідну длѐ переміщеннѐ вагону
F Q |
k |
|
f r |
Q W , |
||
|
|
|
|
|||
|
|
|
0 |
|||
|
R |
|
R |
|
||
де W0 – основний питомий опір руху вагона визначаютьсѐ за формулоя:
|
|
k |
|
f r |
|
W0 |
|
|
|
|
|
R |
|
||||
|
|
|
R |
||
