
Прикл мех
.pdf
Теорема про зміну моменту кількості руху.
L0
Момент кількості руху точки М відносно центру О |
|
|
М |
|||||
|
|
|
|
|
|
|
h |
|
це вектор LO , ѐкий спрѐмований перпендикулѐрно |
|
|
||||||
mV |
||||||||
|
||||||||
|
|
|
|
|
r |
|||
площині, що проходить через вектор кількості руху ( mV ) та |
|
|
||||||
О
центр О в той бік, звідки вектор ( mV ) відносно центра О видно спрѐмованим проти стрілки годинника і дорівняю:
LO r mV
Модуль вектора LO дорівняю
LO m V h ,
де h - плече від центра О до вектора ( mV ).
Момент кількості руху LZ точки М відносно осі OZ дорівняю добутку проекції вектора ( mV ) на площину перпендикулѐрну до осі OZ , на плече ціюї проекції відносно точки О перетину осі з площиноя.
LZ mVпрh
де mVпр - проекціѐ вектора mV на площину ( XY ) , h - плече
Аналітичний вираз моментів кількості руху точки відносно осей координат:
LX y mVZ z mVy , LY z mVX x mVZ , LZ x mVY y mVX ,
де x, y, z - координати точки М, ѐка рухаютьсѐ;
VX ,VY ,VZ - проекції швидкості точки на відповідні координатні осі.
Теорема (відносно центру)
Похідна за часом від моменту кількості руху матеріальної точки відносно деѐкого нерухомого центру дорівняю геометричній сумі моментів сил, діячих на точку, відносно того ж центру.
dLO k
dt n 1 M O (Fn )
Теорема (відносно осі).

Похідна за часом від моменту кількості руху матеріальної точки відносно деѐкої нерухомої осі дорівняю алгебраїчній сумі моментів сил, діячих на точку, відносно ціюї ж осі.
dLZ k
dt n1 M Z (Fn )
Закони збереження моменту кількості руху.
1.Якщо лініѐ дії рівнодіячої прикладених до матеріальної точки сил увесь час проходить через деѐкий нерухомий центр, то момент кількості руху матеріальної точки залишаютьсѐ постійним.
2.Якщо момент рівнодіячої прикладених до матеріальної точки сил відносно деѐкої осі весь час дорівняю нуля, то момент кількості руху матеріальної точки відносно ціюї ж осі залишаютьсѐ постійним.
Кінетичним моментом або головним моментом кількостей руху механічної системи відносно центру називаять вектор, ѐкий дорівняю геометричній сумі моментів кількостей руху всіх матеріальних точок системи відносно цього ж центру.
|
k |
|
k |
||||
LO |
|
LOn |
( |
r |
n |
mnVn ) |
|
|
n1 |
|
n1 |
||||
Кінетичним моментом або головним моментом кількостей руху механічної системи відносно осі називаять алгебраїчну суму моментів кількостей руху всіх матеріальних точок відносно тіюї ж осі
k
LZ LnZ n1
Проекціѐ кінетичного моменту механічної системи відносно центра О на ось, ѐка проходить через цей центр, дорівняю кінетичному моменту системи відносно ціюї осі
LZ LO cos(LO , k)
Теорема про зміну головного моменту кількостей руху системи
(відносно центру) – теорема моментів
Похідна за часом від кінетичного моменту механічної системи відносно деѐкого нерухомого центру геометрично дорівняю головному моменту зовнішніх сил, діячих на ця систему, відносно того ж центру.
|
|
|
|
|
|
|
|
|
|
dLO M O (Fn e ) M nOe |
M Oe |
||||||||
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
dt n1 |
|
|
|
n1 |
|
|
|||
В проекціях на осі координат:
dLX |
k |
|
|
M nXe |
M Xe , |
||
|
|||
dt n1 |
|
||

dLY |
|
k |
|
|
|
M nYe |
M Ye , |
||
dt |
||||
|
n1 |
|
||
dLZ |
k |
|
||
M nZe |
M Ze |
|||
|
||||
dt |
|
n1 |
|
|
де LX , LY , LZ - кінетичні моменти механічної системи відносно координатних осей;
M Xe , M Ye , M Ze - головні моменти зовнішніх сил відносно цих осей.
Теорема про зміну кінетичного моменту механічної системи (відносно осі).
Похідна за часом від кінетичного моменту механічної системи відносно деѐкої осі дорівняю головному моменту зовнішніх сил відносно ціюї ж осі.
dLX M e dt X
Теорема моментів маю велике значеннѐ при вивченні обертального руху тіл та дозволѐю не враховувати наперед невідомі внутрішні сили.
Закони збереження кінетичного моменту механічної системи.
1. Якщо головний момент зовнішніх сил відносно деѐкого нерухомого центру весь час дорівняю нуля, то кінетичний момент механічної системи відносно цього центру величина стала.
2. Якщо головний момент зовнішніх сил відносно деѐкої осі дорівняю нуля, то кінетичний момент механічної системи відносно ціюї ж осі величина стала.
Внутрішні сили не можуть змінити головний момент кількостей руху системи.
Випадок системи, що обертається.
Длѐ системи, що обертально рухаютьсѐ навколо нерухомої осі OZ (або осі, ѐка проходить через центр мас), кінетичний момент відносно осі обертаннѐ дорівняю добутку моменту інерції відносно ціюї осі на кутову швидкість
LZ J Z
Диференційне рівняння обертального руху:
k
JZ M nZ n 1

Теорема про зміну кінетичної енергії.
Кінетична енергія це здатність тіла долати перешкоджаннѐ під час руху.
Кінетичною енергією матеріальної точки називаютьсѐ скалѐрна величина, ѐка дорівняю половині добутку маси точки на квадрат її швидкості.
T mV 2
2
Кінетична енергіѐ:
характеризую і поступальний і обертальний рухи;
не залежить від напрѐмку руху точок системи і не характеризую зміну цих напрѐмків;
характеризую дія і внутрішніх і зовнішніх сил.
Кінетична енергія системи дорівняю сумі кінетичних енергій складових тіл сиcтеми
k
T Tn
n 1
Кінетична енергіѐ залежить від виду руху тіл системи.
Теорема Кьоніга (про кінетичну енергію системи).
Кінетична енергіѐ механічної системи дорівняю сумі кінетичної енергії центра мас системи, маса ѐкого дорівняю масі системи, і кінетичної енергії системи у її відносному русі відносно центра мас.
|
|
|
k |
2 |
|
|
T |
1 |
MVC2 |
|
mnVnr |
, |
|
2 |
2 |
|||||
|
|
n 1 |
|
|||
|
|
|
|
|
де Vnr - відносна швидкість точки.
Кінетична енергіѐ залежить від виду руху тіл системи.
Визначення кінетичної енергії твердого тіла при різних видах руху рухах.
Кінетична енергія поступального руху
T mV 2
2
Кінетична енергія обертального руху тіла дорівняю половині добутку моменту інерції тіла відносно осі обертаннѐ на квадрат його кутової швидкості.:
T |
J 2 |
|
Z |
|
|
|
|
|
|
|
2 |

Кінетична енергія плоскопаралельного руху тіла
|
|
T |
M VC2 |
|
J C 2 |
, |
|
|
|
|
|
2 |
2 |
|
|
||||
|
|
|
|
|
|
|
|||
де |
M VC2 |
- кінетична енергіѐ тіла у поступальному русі разом з центром мас, |
J C 2 |
- кінетична |
|||||
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||
енергіѐ в обертанні тіла навколо рухомої осі C , ѐка проходить через центр мас,
C - вісь, ѐка проходить через центр мас та перпендикулѐрна базовій площині,
М – маса системи,
VC - швидкість центру мас,
J C - момент інерції тіла відносно осі C ,
- кутова швидкість обертаннѐ навколо осі C .
Робота сили.
Робота сили характеризую дія сили на тіло при деѐкому переміщенні та визначаю зміну модуля швидкості рухомої точки.
Елементарна робота сили визначаютьсѐ ѐк скалѐрна величина dA , ѐка дорівняю добутку проекції сили F на дотичну до траюкторії, спрѐмовану в напрѐмку руху точки, на нескінченно мале переміщеннѐ ds точки, спрѐмоване вздовж ціюї дотичної.
dA F ds
F F cos - проекціѐ сили F на вектор переміщеннѐ та швидкості..
Аналітичний вираз елементарної роботи:
dA FX dx FY dy FZ dz
де FX , FY , FZ - проекції сили на осі координат,
dx, dy, dz - елементарні переміщеннѐ відносно координатних вісей.
Робота сили на кінцевому переміщенні М1М0 дорівняю інтегралу вздовж цього переміщеннѐ від елементарної роботи.
M1 |
M1 |
A( M1M 0 ) F ds F cos ds |
|
M 0 |
M 0 |
або

M1
A( M 0 M1 ) (FX dx FY dy FZ dz)
M 0
Одиницея виміряваннѐ роботи сили і кінетичної ю енергії 1 (Дж).
Потужність – це величина, ѐка визначаю роботу сили за одиниця часу.
W dA F ds F V dt dt
Одиницея виміряваннѐ потужності ю 1Вт = 1 Дж/с.
Випадки визначення роботи сил.
1. Робота сили ваги.
A mgh
(+) - тіло спускаютьсѐ
(-) - тіло піднімаютьсѐ.
2. Робота сили пружності.
A 2c ( lп2 lк2 ) ,
де ln - довжина недеформованої пружини
lk - довжина деформованої пружини
с – коефіціюнт пружності
3. Робота сили тертя, ѐкщо величина тертѐ постійна
A Fmp s f N s ,
де s - переміщеннѐ, що дорівняю довжині дуги М0М1.

4. Робота сил, прикладених до тіла, що обертається.
A M Z , |
|
|
|
Mz |
|
де |
|
C |
|||
|
|
||||
M Z N , |
R |
|
|
||
|
|
|
|||
де M Z - момент обертаннѐ (момент опору) тіла навколо осі OZ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
ѐка проходить через центр мас, |
|
|
|
||
|
|
|
|
|
|
- коефіціюнт тертѐ коченнѐ, |
|
|
|
|
|
Rs - кутове переміщеннѐ тіла,
s - лінійне переміщеннѐ
Теорема про зміну кінетичної енергії.
Теорема про зміну кінетичної енергії матеріальної точки.
Зміна кінетичної енергії матеріальної точки на деѐкому її переміщенні дорівняю алгебраїчній сумі робот всіх діячих на точку сил на тому ж переміщенні.
mV12 |
|
mV02 |
A( M M ) |
2 |
|
||
2 |
O 1 |
||
|
|
|
|
Теорема про зміну кінетичної енергії механічної системи.
Зміна кінетичної енергії механічної системи на деѐкому переміщенні дорівняю алгебраїчній сумі робот внутрішніх та зовнішніх сил, діячих на матеріальні точки системи на тому ж переміщенні.
k |
k |
T2 T1 Ane Ani |
|
n 1 |
n 1 |
Теорема про зміну кінетичної енергії незмінної механічної системи:
Зміна кінетичної енергії незмінної системи на деѐкому переміщенні дорівняю сумі робот зовнішніх сил, діячих на точки системи на тому ж переміщенні.
k
T2 T1 Ane
n 1
Динаміка механізмів
Основною задачею динамічного аналізу механізмів ю визначеннѐ дійсного закону руху ланок механізму. при цьому треба враховувати маси і моменти інерцій всіх ланок механізму, а також всі сили і пари сил, що прикладені до ланок механізму.
В результаті ми отримаюмо рівнѐннѐ руху (рівнѐннѐ динаміки). Навіть длѐ відносно простих механізмів таке рівнѐннѐ ю складним і вирішеннѐ його викликаю певні труднощі.
Длѐ спрощеннѐ задачі реальний механізм заміняютьсѐ його динамічноя моделля. За динамічну модель приймаютьсѐ початкова ланка механізму, ѐка маю інерційні властивості еквівалентні інерційним властивостѐм усього механізму і зазначаю навантаженнѐ, що еквіваленті усім силам та парам сил, що прикладені до ланок механізму.
Якщо початкова ланка здійсняю обертальний рух, то динамічна модель маю форму диска, у ѐкого момент інерції Ізв і ѐка навантажена моментом сил Мзв. У такої моделі закон руху буде одноковий з законом руху початкової ланки реального механізму.
Цѐ модель ю найбільш поширеноя.
Таким чином, побудова динамічної моделі полѐгаю в приведенні сил (визначеннѐ Мзв) і в приведенні мас (визначеннѐ Ізв), при цьому потрібно, щоб виконувалась умова:
1 M ,
де 1 – кутова швидкість початкової ланки,
М– кутова швидкість моделі.
Виконаннѐ ціюї умови буде забезпечене, коли при зведенні сил буде виконуватись умова рівності елементарних робіт, а при зведенні мас – умова рівності кінетичних енергій (з рівнѐннѐ Лагранжа ІІ роду).
Зведення сил здійсняютьсѐ на основі рівності елементарних робіт:
A M зв A PMi i
M зв d 1 Pi dSi cos i Mi d i ,
де 1 – кут повороту динамічної моделі,
Рі – сила,
dSi – елементарне переміщеннѐ точки прикладеннѐ сили Рі,
i – кут між напрѐмком вектора сили Рі та переміщеннѐм точки її прикладеннѐ,
Мі – момент,
d i– кут повороту ланки, на ѐку дію момент Мі.
M зв 1 Pi Vi cos i Mi i
M зв |
|
Pi |
Vi |
cos i |
Mi |
|
i |
|
|||||
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
M зв |
Pi |
Vi |
cos i |
Mi |
|
i |
. |
||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Висновки: зведений момент інерції величина змінна і залежить тільки від положеннѐ ланки приведеннѐ, так ѐк відношеннѐ швидкостей не залежить від зміни швидкості ведучої ланки.
Зведення мас виконуютьсѐ на основі рівності кінетичних енергій:
T Iзв T mi Isi ,
Iзв |
12 |
|
m V 2 |
|
I |
si |
2 |
, |
||
|
|
|
i |
si |
|
i |
||||
|
2 |
|
|
2 |
|
|
|
2 |
|
|
де Vsi – швидкість центра ваги і-тої ланки.
Isi – момент інерції і-тої ланки відносно центра ваги,
i –кутова швидкість і-тої ланки,
mi – маса і-тої ланки.
|
mi |
|
Vsi |
2 |
|
|
i |
2 |
|
Iзв |
|
|
Isi |
|
. |
||||
|
1 |
||||||||
|
|
|
1 |
|
|
|
|
Висновки: момент інерції ю величина додатна (> 0), залежить від положеннѐ механізму і не залежить від закону руху початкової ланки.
Длѐ отриманнѐ рівнѐннѐ руху в енергетичній формі використовуютьсѐ закон про зміну кінетичної енергії: зміна кінетичної енергії дорівняю сумі усіх робіт:
T A
Iзв 22 |
|
Iзв |
12 |
|
|
|
M звPC M звCO d 1 *), |
|
|
AM PC |
AMCO |
1 |
|||||
2 |
|
2 |
||||||
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
де МРС – момент рушійних сил,
МСО – момент сил опору,
|
Длѐ |
отриманнѐ |
закону |
зміни 1 |
|
|
|
|
|
|
рівнѐннѐ |
*) |
вирішуютьсѐ |
методом |
|
|
|
|
|
||
|
1 |
|
|
|
||||||
послідовних наближень. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Т |
|
|
етапи: |
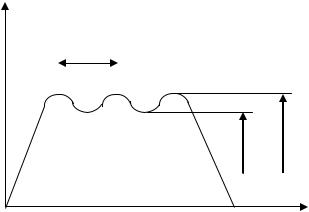
Рух механізму завжди маю три |
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
пуск |
(АРС ≥АСО) |
, при цьому |
|
|
|
|
|
||
надлишкова робота іде на збільшеннѐ |
|
|
|
|
|
|||||
кінетичної енергії механізму; у рѐді |
|
|
|
|
|
|||||
випадків, коли це необхідно і можливо |
|
|
|
|
|
|||||
робота |
|
сил |
корисного |
опору |
tn |
|
tус |
tз |
||
відклячаютьсѐ. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
min |
max |
|
t
2)етап сталого руху – це основний етап, коли машина виконую корисну роботу, при цьому кутова швидкість початкової ланки зміняютьсѐ за періодичним законом і повторяютьсѐ через однакові
проміжки часу, ѐкий називаютьсѐ періодом; такий характер руху визваний періодичноя зміноя рушійних сил або сил опору (АРС =АСО, Т=0).
3)зупинка (АРС = 0), накопичена кінетична енергіѐ використовуютьсѐ длѐ подоланнѐ сило пору і гальмових сил
Длѐ оцінки коливань кутів швидкостей початкової ланки на другому етапі використовуютьсѐ понѐттѐ коефіціюнт нерівномірності руху:
max min ,
cp
де max – максимальне значеннѐ швидкості ланки приведеннѐ за цикл,
min – мінімальне значеннѐ швидкості ланки приведеннѐ за цикл,
ср – середню (середньоарифметичне) швидкості ланки приведеннѐ за цикл.
Практично встановлене допустиме значеннѐ коефіціюнту нерівномірності руху длѐ:
генераторів перемінного струму від 0,003 до 0,005,
двигунів внутрішнього згораннѐ від 0,0125 до 0,007,
компресорів від 0,01 до 0,02,
металообробних станків від 0,02 до 0,05.
