3.1.2 Розкладання сум квадратів

Відповідно до основної ідеї дисперсійного аналізу розкладемо суму S квадратів відхилень спостережень від загального середнього на компоненти, що відповідають перерахованим факторам.

де

(3.5)

- загальна сума квадратів, характеризує розсіювання окремих спостережень у загальній сукупності за рахунок впливу усіх факторів,

(3.6)

- сума квадратів відхилень "усередині серій". Сума характеризує розсіювання окремих спостережень за рахунок впливу фактора випадковості.

(3.7)

- сума квадратів відхилень “між рядками”. Сума характеризує розсіювання середніхза рядками в результаті дії фактора випадковості (з дисперсією середнього рядка), фактораx₁ (з дисперсією ) і фактора взаємодії (з дисперсією середнього для кожного рядка).

(3.8)

-сума квадратів відхилень "між стовпцями". Сума характеризує розсіювання середніхпо стовпцях в результаті дії фактора випадковості (з дисперсією середнього стовпця), фактораx₂ (з дисперсією ) і фактора взаємодії (з дисперсією стовпця),

(3.9)

- сума квадратів відхилень "між серіями". Сума характеризує розсіювання середніхсерій в результаті дії фактора випадковості (з дисперсією середнього серії) і фактора взаємодії (з дисперсією ).

3.1.3 Оцінка дисперсій

Суми квадратів S, S₀, S₁, S₂, S₁₂, розділені кожна на відповідну їй кількість ступенів свободи , ₀, ₁, ₂, ₁₂, дають незміщені оцінки диспер-сії відтворення ².

1) вибіркова загальна дисперсія за всіма спостереженнями

(3.10)

з кількістю ступенів свободи

,

2) вибіркова дисперсія розсіювання "усередині серій" або залишкова оцінка є середньозваженою дисперсією за всіма серіями спостережень

(3.11)

з кількістю ступенів свободи

3) вибіркова дисперсія розсіювання "між рядками"

(3.12)

з кількістю ступенів свободи

4) вибіркова дисперсія розсіювання "між стовпцями"

(3.13)

з кількістю ступенів свободи

5) вибіркова дисперсія розсіювання "між серіями"

(3.14)

з кількістю ступенів свободи

Кількість ступенів свободи перевіряється за співвідношенням

(3.15)

3.1.4. Оцінка впливу факторів

Аналіз значимості впливу факторів x₁, x₂ та їхньої взаємодії x₁, x₂ проводиться за критерієм Фішера при обраному рівні значимості q у такому порядку:

1) вплив факторів x₁ і x₂ відповідно з дисперсіями

(3.16)

визнається значним якщо виявиться значною відповідно, відмінністьвід івід, тобто якщо відповідний критерій

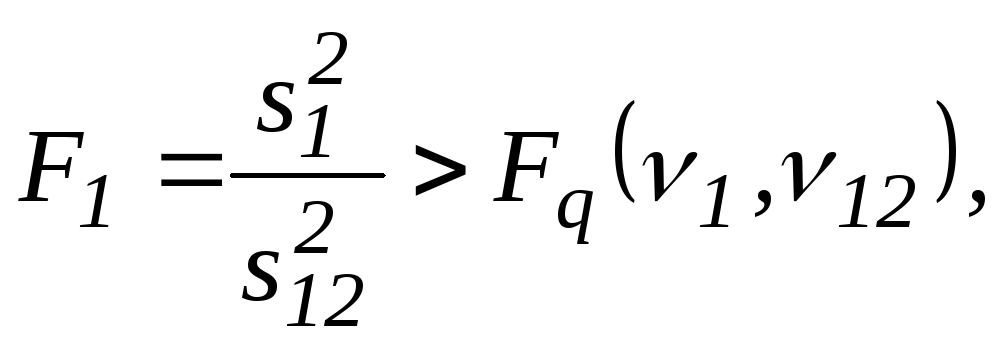
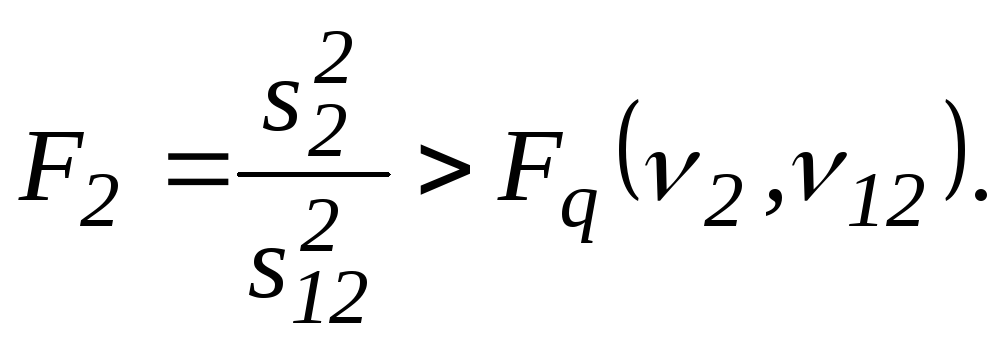(3.17)

Якщо одне з цих дисперсійних відношень незначне, тобто вплив відповідного фактора, незначне або, то для дисперсіїми одержимо дві оцінки іабоі,відповідно, які можна об’єднати в зведену оцінку

(3.18)

або

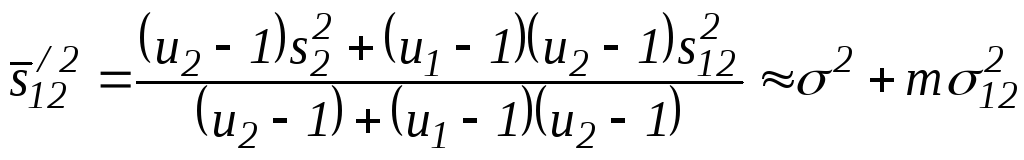(3.19)

з великою кількістю ступенів свободи

Якщо два дисперсійних відношення, тобто впливи обох факторів, незначні і, то оцінки,ідля дисперсіїможна об’єднати в зведену

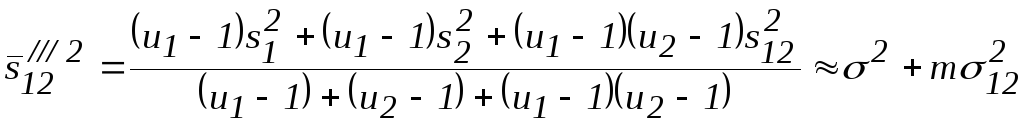(3.20)

з великою кількістю ступенів свободи

2) вплив взаємодії x₁x₂ з дисперсією

(3.21)

визнається значним якщо відмінність і виявиться значною, тобто, якщо критерій

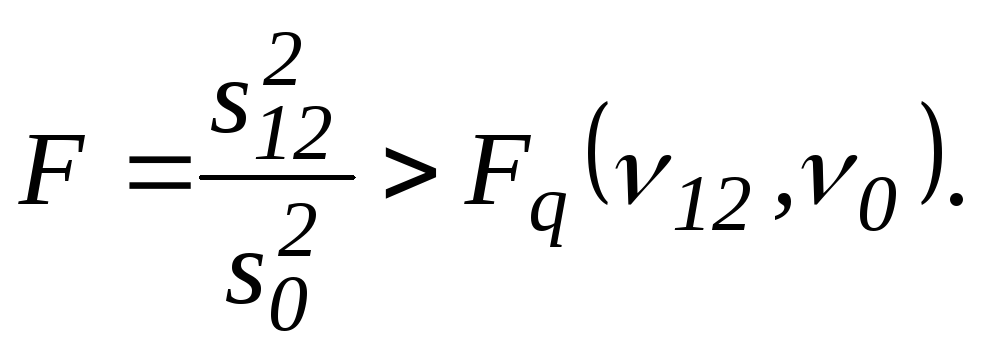(3.22)

У протилежному випадку вплив взаємодії вважається незначним і обидві оцінки і для² можна об’єднати в одну

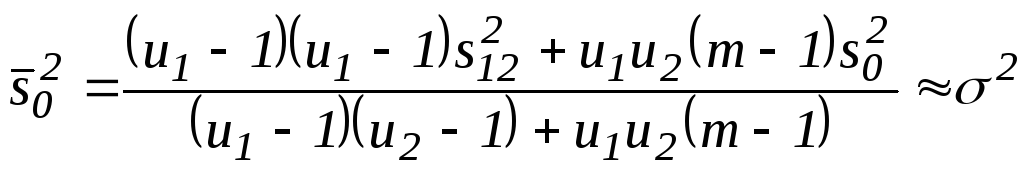(3.23)

з великою кількістю ступенів свободи

Якщо вплив факторів x₁, x₂ і їхньої взаємодії x₁x₂ незначні, то дисперсію відновлення можна оцінити вибірковою загальною дисперсією s².