
- •"Томский политехнический университет"
- •А.В. Маслов методы экономико-математического моделирования
- •Предисловие
- •Тема 1 Предмет экономико-математического моделирования
- •Моделирование как метод научного познания
- •Классификация экономико-математических моделей
- •Этапы экономико-математического моделирования
- •Взаимосвязи этапов
- •Моделирования
- •Тема 2 Системный подход к изучению экономических явлений Системный анализ как научная дисциплина
- •Вычислительная техника в системном анализе
- •Системный подход Основные определения: элементы, связи, система
- •Принципы системного подхода
- •Об использовании принципов системного подхода
- •Тема 3 Математические методы
- •И основные классы задач оптимизации
- •Общая постановка математической модели задач
- •Оптимизации
- •Тема 4 Линейное программирование
- •Пример решения станковой задачи
- •Симплекс-метод решения задач линейного программирования
- •Свойства опорных решений
- •Решение задач линейного программирования симплекс-методом
- •Конечность симплекс-метода
- •Метод искусственного базиса для отыскания начального опорного решения
- •Двойственность в линейном программировании
- •Виды математических моделей двойственных задач
- •Тема 5 Целочисленное программирование
- •Постановка задачи и метод решения
- •Метод Гомори
- •Составление дополнительного ограничения (сечения Гомори)
- •Тема 6 Транспортная задача
- •Построение первоначального опорного плана
- •Метод минимальной стоимости
- •Определение оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке
- •Тема 7 Нелинейное программирование
- •Теорема Куна – Таккера
- •Список литературы
- •Оглавление
- •Часть I
Теорема Куна – Таккера
Теорема 7.2. Для
задачи выпуклого программирования
(7.4)–(7.6), множество допустимых решений
которой обладает свойством регулярности,
план
![]() является оптимальным планом тогда и
только тогда, когда существует такой
вектор
является оптимальным планом тогда и
только тогда, когда существует такой
вектор
![]() ,
что
,
что![]() – седловая точка функции Лагранжа.
– седловая точка функции Лагранжа.
Если предположить,
что целевая функция
![]() и функции
и функции![]() непрерывны и дифференцируемы, то теорема
Куна-Таккера может быть дополнена
аналитическими выражениями, определяющими
необходимое и достаточное условие того,
чтобы точка
непрерывны и дифференцируемы, то теорема
Куна-Таккера может быть дополнена
аналитическими выражениями, определяющими
необходимое и достаточное условие того,
чтобы точка![]() была седловой точкой функции Лагранжа,
т.е. являлась решением задачи выпуклого
программирования. Эти выражения имеют
следующий вид:
была седловой точкой функции Лагранжа,
т.е. являлась решением задачи выпуклого
программирования. Эти выражения имеют
следующий вид:

где
![]() и
и![]() – значения
соответствующих частных производных
функции Лагранжа, вычисленных в седловой
точке.
– значения
соответствующих частных производных
функции Лагранжа, вычисленных в седловой
точке.
Теорема
Куна-Таккера в теории нелинейного
программирования занимает центральное
место. Она справедлива и для задач так
называемого квадратичного программирования,
т.е. где целевая функция
![]() при ограничениях:
при ограничениях:
![]() .
.
В общем случае решения задач нелинейного программирования для определения глобального экстремума задачи не существует эффективного вычислительного метода, если неизвестно, что любой локальный экстремум одновременно является и глобальным. Так, в задаче выпуклого и квадратичного программирования множество допустимых решений выпукло, то, если целевая функция вогнута, любой локальный максимум является также и глобальным.
Пример
7.3.
С помощью теоремы Куна-Таккера найдём
![]() при ограничениях
при ограничениях
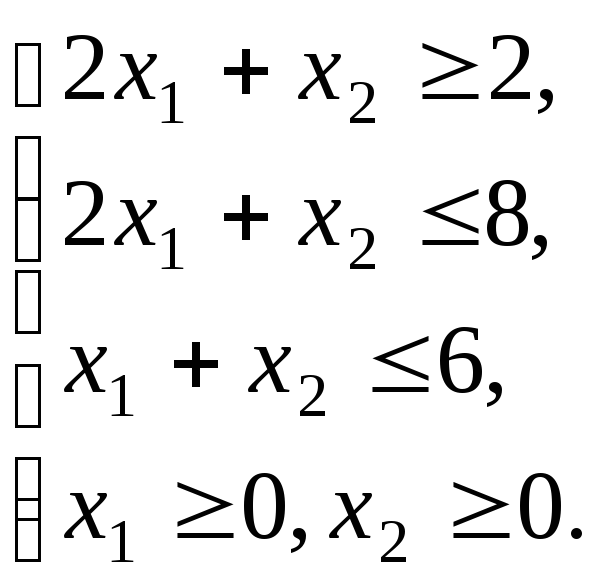
Решаем
графически (рис. 7.2) и находим:
![]() ;
;![]() ;
;![]() (более подробно решение см. ниже). Покажем,
что существует векторY0
0,
при котором в точке оптимума выполняются
условия Куна-Таккера. Составим функцию
Лагранжа:
(более подробно решение см. ниже). Покажем,
что существует векторY0
0,
при котором в точке оптимума выполняются
условия Куна-Таккера. Составим функцию
Лагранжа:
![]() .
.
Находим:
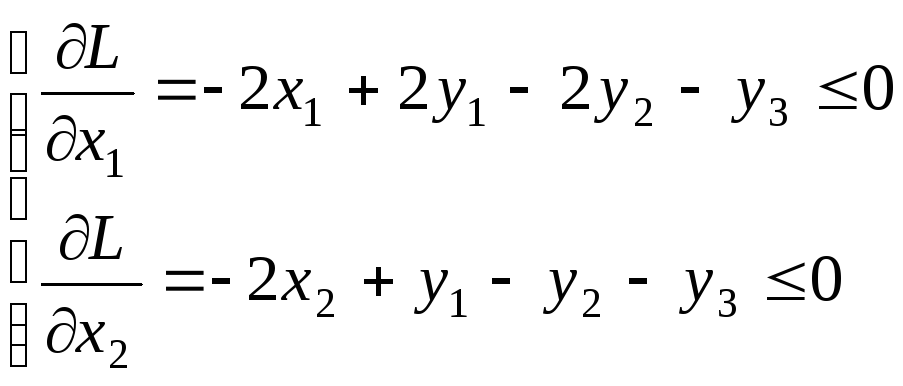
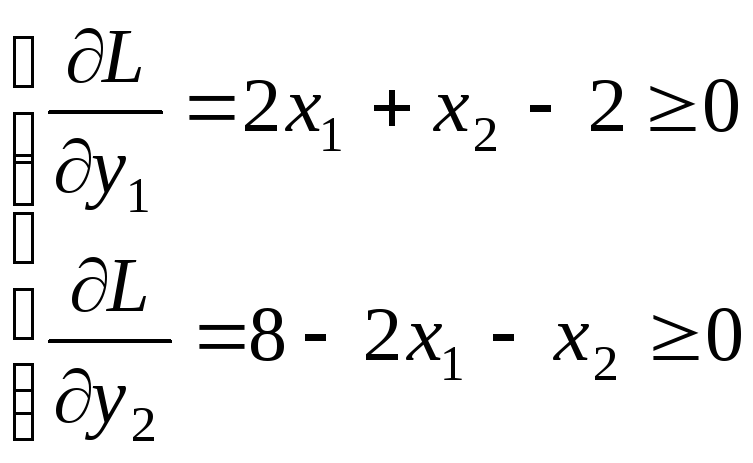
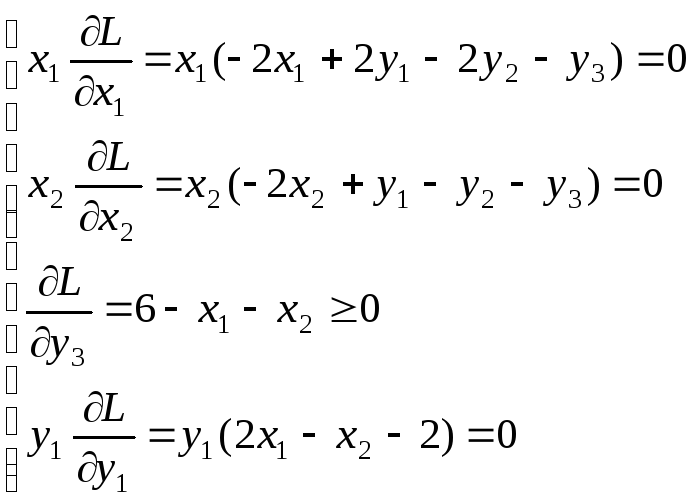
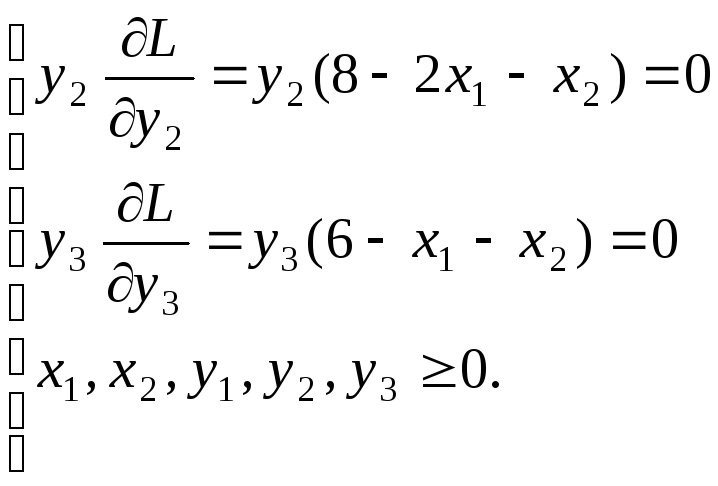
Решение
![]() находим из системы:
находим из системы: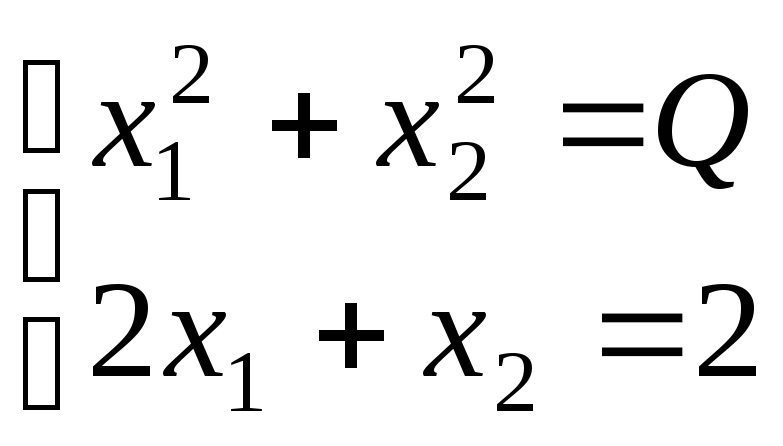 .
Из второго уравнения
.
Из второго уравнения![]() подставляем в первое уравнение системы.
Дифференцируем по
подставляем в первое уравнение системы.
Дифференцируем по![]() :
:![]() .
В выражения
.
В выражения![]() и
и![]() подставляем значения
подставляем значения![]() и
и![]() .
Имеем значения частных производных
больше нуля, а по условию должны быть
равно нулю, тогда
.
Имеем значения частных производных
больше нуля, а по условию должны быть
равно нулю, тогда
![]() =0
и
=0
и
![]() =0.
С другой стороны,
=0.
С другой стороны,![]() может принимать ненулевые значения,
т.к.
может принимать ненулевые значения,
т.к.
![]() отсюда
отсюда
![]() ;
все
;
все
![]() т.е. условия Куна-Таккера выполняются,
следовательно, эта точка – точка
экстремума.
т.е. условия Куна-Таккера выполняются,
следовательно, эта точка – точка
экстремума.
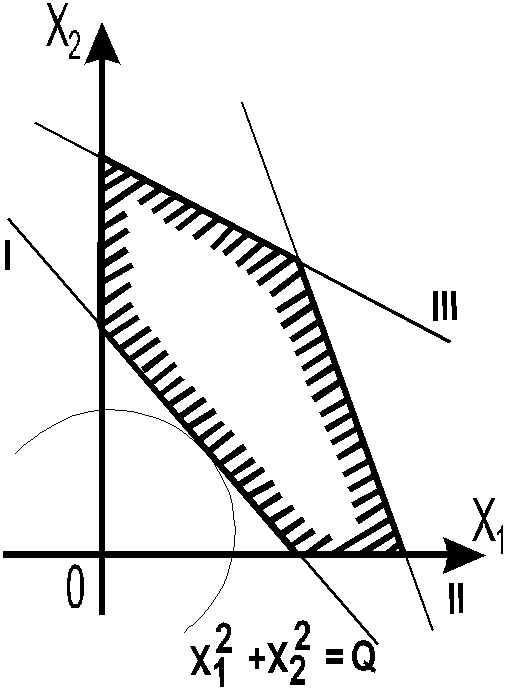
Рис.7.2. Графическое решение задачи нелинейного
программирования примера 7.3
Необходимое
условие оптимальности
для задачи нелинейного программирования
можно сформулировать следующим образом.
Пусть
![]() – оптимальное решение задачи (7.4)–(7.6),
причём функции
– оптимальное решение задачи (7.4)–(7.6),
причём функции![]() ,
,
![]() ,
,
![]() дифференцируемы в этой точке. Если
дифференцируемы в этой точке. Если![]() – неособая точка допустимого множества
задачи (7.4)–(7.6), то она является точкой
Куна-Таккера этой задачи.
– неособая точка допустимого множества
задачи (7.4)–(7.6), то она является точкой
Куна-Таккера этой задачи.
Таким образом,
если допустимое множество
![]() задачи (7.4)-(7.6) не имеет особых точек, а
функцииF(М),
gi(М),
(
задачи (7.4)-(7.6) не имеет особых точек, а
функцииF(М),
gi(М),
(![]() )
дифференцируемы во всех точках
)
дифференцируемы во всех точках
![]() ,
то оптимальное решение этой задачи
следует искать среди точек Куна-Таккера.
,
то оптимальное решение этой задачи
следует искать среди точек Куна-Таккера.
Как известно из математического анализа, особой точкой множества допустимых решений системы линейных уравнений и неравенств вида
![]() ,
,
т. е. множества допустимых решений
![]()
если в точке
![]() линейно зависимы градиенты тех функций
линейно зависимы градиенты тех функций
![]() ,
которые в ней обращаются в
,
которые в ней обращаются в![]() .
Например,
.
Например,![]() – особая точка множества
– особая точка множества
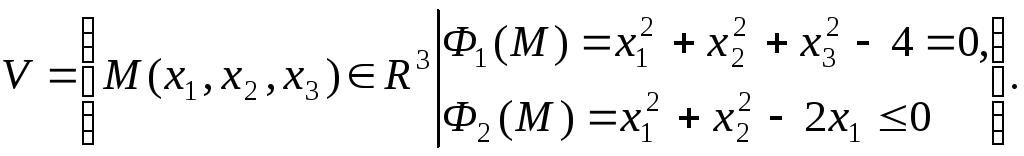
Действительно,
![]()
Таким образом,
![]() –
линейно зависимая система.
–
линейно зависимая система.
Градиент функции
![]() – это вектор, координаты которого
соответственно равны значениям частных
производных функции
– это вектор, координаты которого
соответственно равны значениям частных
производных функции![]() в точкеM0.
Этот вектор показывает направление
быстрейшего роста функции.
в точкеM0.
Этот вектор показывает направление
быстрейшего роста функции.
Необходимое условие оптимальности малопригодно для решения большинства задач нелинейного программирования, т.к. лишь в редких случаях удается найти все точки Куна-Таккера задачи нелинейного программирования.
Достаточное
условие оптимальности
для задачи нелинейного программирования:
если
![]() – седловая точка функции Лагранжа для
задачи (7.4)–(7.6), то
– седловая точка функции Лагранжа для
задачи (7.4)–(7.6), то![]() является оптимальнымрешением
этой задачи.
является оптимальнымрешением
этой задачи.
Это условие в общем случае не является необходимым: функция Лагранжа может не иметь седловых точек, в то же время исходная задача нелинейного программирования обладает оптимальным решением.
Известны различные
методы, позволяющие найти оптимальное
решение задачи нелинейного программирования
приближённо. Однако эти методы дают
достаточно хорошее приближение лишь
для задачи выпуклого программирования,
где всякий локальный экстремум является
одновременно и глобальным. В общем
случае под градиентными
методами
понимают методы, в которых движение к
точке оптимума функции совпадает с
направлением градиента этой функции,
т.е. начиная с некоторой точки
![]() осуществляется последовательный переход
к некоторым другим точкам до тех пор,
пока не выявится приемлемое решение
исходной задачи. При этом градиентные
методы могут быть подразделены на 2
группы.
осуществляется последовательный переход
к некоторым другим точкам до тех пор,
пока не выявится приемлемое решение
исходной задачи. При этом градиентные
методы могут быть подразделены на 2
группы.
К первой группе относятся методы, при использовании которых исследуемые точки не выходят за пределы области допустимых решений задачи. Наиболее распространенным из таких методов является метод Франка-Вольфа (Вулфа). К числу таких методов относится метод проектируемых градиентов Розена, метод допустимых направлений Зойтендейка.
Ко второй группе относятся методы, при использовании которых исследуемые точки могут как принадлежать, так и не принадлежать области допустимых решений. Однако в результате реализации итерационного процесса находится точка области допустимых решений, определяющая приемлемое решение.
Из таких методов наиболее часто используется метод штрафных функций или метод Эрроу-Гурвица.
При нахождении
решения задач градиентными методами,
в том числе и названными, итерационный
процесс осуществляется до того момента,
пока градиент функции
![]() в очередной точке
в очередной точке![]() не станет равным нулю или же пока
не станет равным нулю или же пока![]() ,
где
,
где![]() – достаточно малое положительное число,
характеризующее точность полученного
решения.
– достаточно малое положительное число,
характеризующее точность полученного
решения.
Решение сложных задач нелинейного программирования градиентными методами связано с большим объёмом вычислений и целесообразно только с использованием ЭВМ.
На примере покажем общий смысл градиентных методов решения задач нелинейного программирования.
Пусть имеется
функция двух переменных
![]() .
Пусть исходные значения переменных
будут
.
Пусть исходные значения переменных
будут![]() ,
а значение функции
,
а значение функции![]() .
Если
.
Если![]() не является экстремумом, то определяют
такие новые значения переменных
не является экстремумом, то определяют
такие новые значения переменных![]() и
и![]() ,
чтобы следующее значение функции
,
чтобы следующее значение функции![]() оказалось ближе к оптимуму, чем предыдущее.
оказалось ближе к оптимуму, чем предыдущее.
Каким же образом
определяется величина приращений
![]() и
и
![]() ?
Для этого в точках
?
Для этого в точках
![]() и
и![]() определяется направление изменения
функции в сторону экстремума с помощью
градиента. Чем больше значение частной
производной, тем быстрее происходит
изменение функции в сторону экстремума.
Поэтому приращения
определяется направление изменения
функции в сторону экстремума с помощью
градиента. Чем больше значение частной
производной, тем быстрее происходит
изменение функции в сторону экстремума.
Поэтому приращения![]() и
и![]() выбирают пропорциональными значению
частных производных
выбирают пропорциональными значению
частных производных![]() и
и![]() в точках
в точках![]() и
и![]() .
Таким образом,
.
Таким образом,
![]() и
и
![]() ,
где
,
где
![]() – величина, называемая шагом, котораяустанавливает
масштаб изменений
– величина, называемая шагом, котораяустанавливает
масштаб изменений
![]() и
и![]() .
.
Пример 7.4.
Пусть необходимо максимизировать функцию
![]() (максимум в точке
(3;2))
(максимум в точке
(3;2))
![]()
![]() .
.
В точке
![]() ,
,![]() при
при![]() имеем
имеем
![]() ;
;
![]() ,
,
откуда
![]() ;
;
![]() ;
;
![]() .
.
Проведём ещё одну
итерацию. В точке
![]() ,
,![]() при
при![]() имеем
имеем
![]() ;
;
![]() ,
,
откуда
![]() ;
;
![]() ;
;
![]() .
.

Рис.7.3. Геометрическая интерпретация двух шагов
градиентного метода для примера 7.4
На рис. 7.3 показано
движение по градиенту, которое было
проведено в данном примере. Отношение
![]() указывает направление изменения функции
в сторону максимума. Если градиент взять
со знаком минус, то будем двигаться в
сторону минимума.
указывает направление изменения функции
в сторону максимума. Если градиент взять
со знаком минус, то будем двигаться в
сторону минимума.
Специфической проблемой градиентных методов является выбор величины шага t. Если задаться малым шагом, то оптимум будем искать очень долго. Если выбрать его значение слишком большим, то оптимум можно "проскочить". Соответствующими методами решается промежуточная задача выбора оптимальной величины шага. Если шаг t определяется приближённо, то, как правило, попадают не в оптимум, а в его зону. Градиентные методы обеспечивают определение локальных оптимумов. При отыскании глобального оптимума с помощью градиента нередко бывает сомнение в том, что найденный оптимум является глобальным. В этом недостаток этого метода при решении задач невыпуклого программирования.
Вопросы для самопроверки
Постановка задачи нелинейного программирования.
Процесс нахождения решения задачи нелинейного программирования с использованием её геометрической интерпретации.
Алгоритм метода Лагранжа решения задачи нелинейного программирования.
Применение метода Лагранжа к решению задачи нелинейного программирования в случае, когда условия связи представляют собой неравенства.
Вспомогательные определения и теоремы, необходимые для рассмотрения центральной теоремы нелинейного программирования – теоремы Куна-Таккера.
Теорема Куна-Таккера.
Необходимое и достаточное условие оптимальности для задачи нелинейного программирования.
Общий смысл градиентных методов приближённого решения задач нелинейного программирования.
Группы градиентных методов приближённого решения задач нелинейного программирования.
