Метод искусственного базиса для отыскания начального опорного решения

Для того чтобы решить задачу линейного программирования в канонической форме, необходимо предварительно найти некоторое начальное опорное решение этой задачи. Сделать это можно методом искусственного базиса.

Рассмотрим задачу линейного программирования в канонической форме:

,

(4.13)

.

Без ограничения общности можно считать, что Для отыскания опорного решения задачи (4.13) строим вспомогательную задачу:

,

(4.14)

.

Свойства вспомогательной задачи.

1. Вспомогательная задача (4.14) всегда имеет опорное решение.

2. Вектор является опорным решением задачи (4.14).

Таким образом, принимая вектор за начальное опорное решение, вспомогательную задачу можно решить симплекс-методом. Пустьоптимальное опорное решение задачи (4.14).

Если тоопорное решение исходной задачи (4.13). Если же среди чиселесть положительные, то исходная задача (4.13) имеет пустое допустимое множество.

Таким образом, всегда можно либо найти опорное решение исходной задачи либо установить её неразрешимость.

Двойственность в линейном программировании

Понятие двойственности. С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется исходной.

Связь исходной и двойственной задач состоит в том, что коэффициенты целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные членысистемы ограничений исходной задачи служат коэффициентами функции цели двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи. Решение двойственной задачи может бытьполучено из решения исходной и наоборот.

В качестве примера рассмотрим задачу использования ресурсов. Пусть предприятие имеет m видов ресурсов в количестве (i=1,2,…,m) единиц, из которых производится n видов изделий. Для производства одной единицы j-й продукции расходуется единицi-го ресурса, а её стоимость составляет единиц. Составить план выпуска продукции, обеспечивающий её максимальный выпуск в стоимостном выражении. Обозначим черезколичество единицj-й продукции. Тогда исходную задачу сформулируем так:

найти вектор , которыйудовлетворяет ограничениям

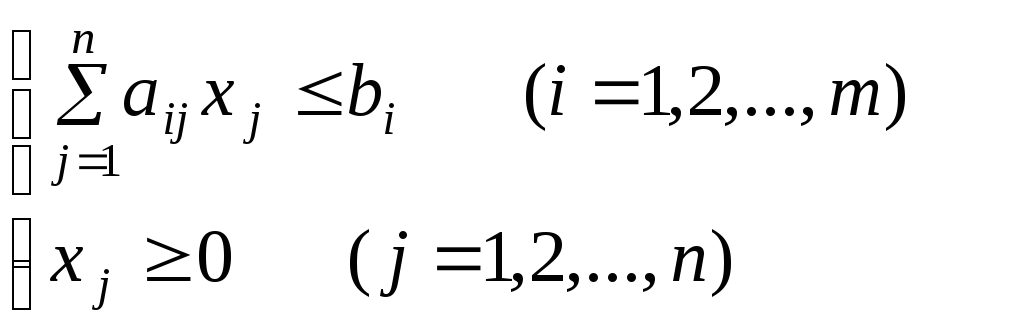
и доставляет максимальное значение линейной функции .

Оценим ресурсы, необходимые для изготовления продукции. За единицу стоимости ресурсов примем единицу стоимости выпускаемой продукции. Обозначим через стоимость единицыi-го ресурса. Тогда стоимость всех затраченных ресурсов, идущих на изготовление единицы j-й продукции, равна . Стоимость затраченных ресурсов не может быть меньше стоимости окончательного продукта (не может появиться из "ничего"), поэтому должно выполняться неравенствоСтоимость всех имеющихся ресурсов выразится величинойИтак, двойственную задачу можно сформулировать следующим образом:

найти вектор двойственных оценок , который удовлетворяет ограничениям

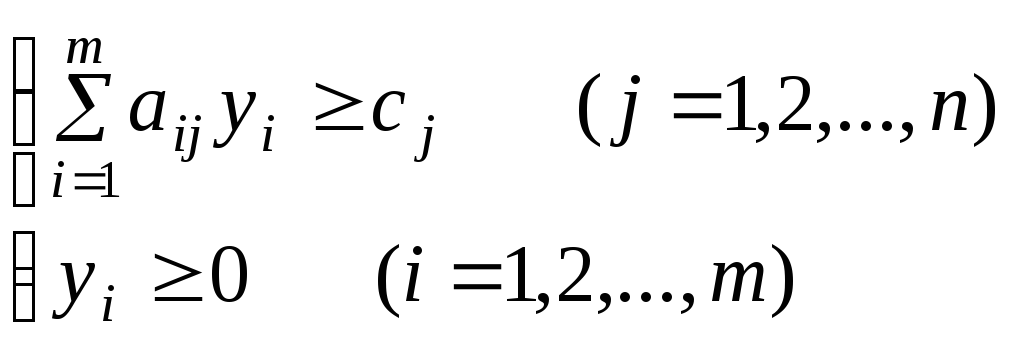
и доставляет минимальное значение линейной функции

Рассмотренные исходная и двойственная задачи могут быть экономически интерпретированы так.

Исходная задача. Сколько и какой продукции необходимо произвести, чтобы при заданных стоимостяхединицы продукции и размерах имеющихся ресурсовмаксимизировать выпуск продукции в стоимостном выражении?

Двойственная задача. Какова должна быть цена единицы каждого из ресурсов, чтобы при заданных количествах ресурсов и величинах стоимости единицы продукции минимизировать общую стоимость затрат?

Переменные называются двойственными оценками или учётными, неявными ценами. В работах Немчинова В.С., Новожилова В.В., Аганбегяна А.Г. их называют объективно обусловленными оптимальными оценками (о.о.о.о.). Им посвящено много работ, поскольку их экономический смысл в этих математических моделях очень важен для экономического анализа производственной ситуации. Например, в нашей задаче использования ресурсов эти оценки показывают степень дефицитности ресурсов. Более того, величина данной двойственной оценки показывает, на сколько возрастёт максимальное значение целевой функции прямой задачи при увеличении количества сырья соответствующего вида на 1 кг.

В результате решения задачи линейного программирования найдётся некий оптимальный план. При подстановке этого решения в задачу обнаружится, что некоторые ресурсы используются полностью, а некоторые останутся неиспользованными. Двойственные оценки соответствующих ресурсов будут положительными и нулевыми. Последнее будет наблюдаться там, где ресурсы не используются полностью. Причём самое узкое место – наиболее дефицитный ресурс – будет иметь двойственную оценку с наибольшим положительным значением. Знание этого "узкого" места уже может влиять на принятие какого-либо управленческого решения. Эти двойственные оценки имеют ещё несколько экономических интерпретаций, например, как средство балансировки между суммарными затратами и результатами.

Многие задачи линейного программирования первоначально ставятся в виде исходных или двойственных задач, поэтому имеет смысл говорить о паре двойственных задач линейного программирования.

В зависимости от вида ограничений исходные задачи линейного программирования двойственные задачи могут быть несимметричными и симметричными. В несимметричных двойственных задачах система ограничений исходной задачи задаётся в виде неравенств, причём в последней переменные могут быть и отрицательными. Для простоты постановку задачи условимся записывать в матричной форме.

Исходная задача. Найти матрицу-столбец , который удовлетворяет ограничениями минимизирует линейную функцию

Двойственная задача. Найти матрицу-строку которая удовлетворяет ограничениями максимизирует линейную функцию

В обеих задачах матрица-строка,матрица-столбец,матрица коэффициентов системы ограничений. Связь между оптимальными планами пары двойственных задач устанавливают следующие теоремы двойственности:

1)(первая теорема двойственности). Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причём для экстремальных значений линейных функций выполняется соотношение Если линейная функция одной из задач не ограничена, то другая не имеет решения.

2)(вторая теорема двойственности). План исходной задачи и пландвойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любогоj=1,2,…,n выполняется равенство 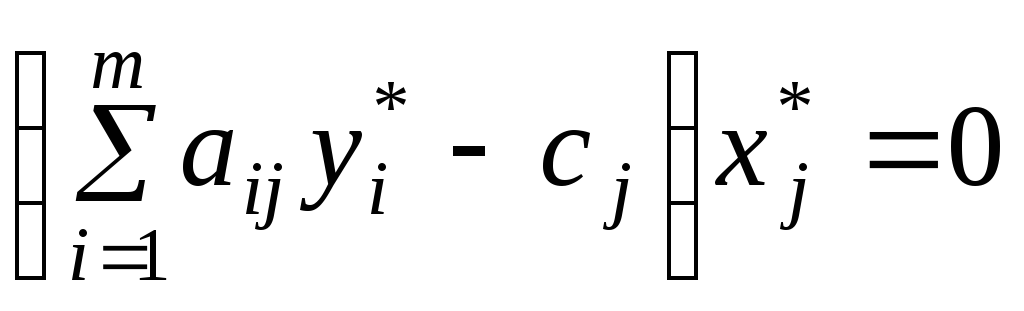. Эти теоремы позволяют при решении одной из двойственных задач находить оптимальный план другой.

Разновидностью двойственных задач линейного программирования являются двойственные симметрические задачи, в которых система ограничений как исходной, так и двойственной задач задаётся неравенствами, причём на двойственные переменные налагается условие неотрицательности.

Исходная задача. Найти матрицу-столбец которая удовлетворяет системе ограниченийи минимизирует линейную функцию

Двойственная задача. Найти матрицу-строку которая удовлетворяет системе ограниченийи максимизирует линейную функциюf=YB.

Систему неравенств с помощью дополнительных переменных можно преобразовать в систему уравнений, поэтому всякую пару симметричных двойственных задач можно преобразовать в пару несимметричных.

Используя симметричность, можно выбрать задачу, более удобную для решения симплекс-методом. Объём задачи, решаемой с помощью ЭВМ, ограничен числом включаемых строк, поэтому задача, довольно громоздкая в исходной постановке, может быть упрощена в двойственной формулировке. При вычислениях без помощи машин использование двойственности упрощает вычисления.