Составление дополнительного ограничения (сечения Гомори)

Пусть оптимальный план, полученный симплекс-методом для задачи (5.1)-(5.3), следующий: и получен на базисе Тогда последняя симплексная таблица имеет следующий вид:

Таблица 5.1

Приведённая к базису симплексная таблица для задачи целочисленного программирования

Предположим, что дробное; тогда некотороетакже дробное (в противном случае задача не имеет целочисленного решения). Обозначим черезицелые части чисели, т.е. наибольшие целые числа, не превосходящие числаи. Тогда величины дробных частейичиселиопределяются как разности:

где и

Например,

.

Так как по условию – неотрицательные целые числа, то и разностьтакже целое неотрицательное число.

Преобразуя это неравенство в уравнение, вычитая из его левой части целую неотрицательную дополнительную переменную умножим уравнение на –1, добавим к последней симплексной таблице и, применяя симплексный метод (желательно двойственный), находим новый план. Если он не является целочисленным, то по последней симплексной таблице составляем новое дополнительное ограничение.

Если в оптимальном плане задачи (5.1)-(5.3) несколько дробных то дополнительное ограничение составляют дляmax. Это ускоряет процесс получения оптимального целочисленного решения.

Рассмотрим геометрический смысл введения дополнительного ограничения (см. рис. 5.2). Пусть в точке A многогранника решений Q функция Z достигает максимального значения Z(A)=max, но координаты точки A – дробные. Тогда введенные ограничения по целочисленности I и II от области Q отсекают область с угловой точкой, координаты которой целочисленные и в которой линейная функция достигает максимального значения.

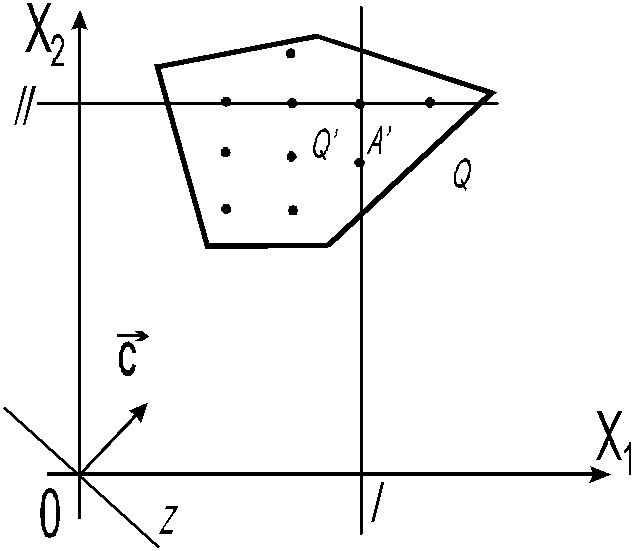
Рис.5.2. Геометрический смысл ограничения Гомори

Метод Гомори рассмотрим на примере следующей задачи.

Пример 5.1. Найти максимальное значение функции

(5.5)

при условиях

	(5.6)
	(5.7)
–целые,	(5.8)

Дать геометрическую интерпретацию решения задачи.

Решение. Для определения оптимального плана задачи (5.5)-(5.8) сначала находим оптимальный план задачи (5.5)-(5.7):

Таблица 5.2

Симплекс-таблица, приведённая к базису

x1	x2	x3	x4	x5
1	1	1	0	0	13
1	-1	0	1	0	6
-3	1	0	0	0	9
3	2	0	0	1	0

базис план – неоптимальный, .

Таблица 5.3

Симплекс-таблица, приведённая к базису

x1	x2	x3	x4	x5
0	2	1	-1	0	7
1	-1	0	1	0	6
0	-2	0	3	1	27
0	5	0	-3	0	-18

, – неоптимальный, базис , .

Таблица 5.4

Симплекс-таблица, приведённая к базису

x1	x2	x3	x4	x5
0	1	1/2	-1/2	0	7/2
1	0	1/2	½	0	19/2
0	0	1	2	1	34
0	0	-5/2	-1/2	0	-71/2

Оптимальный план , базис. Этот оптимальный план не является оптимальным планом задачи (5.5)-(5.8), поскольку две компонентыиимеют нецелочисленное значение. При этом дробные части этих чиселравны между собой. Поэтому для одной из этих переменных составляется дополнительное ограничение. Составим, например, такое ограничение для переменной(чаще берут первую строку). Из последнейсимплекс-таблицы имеем:

.

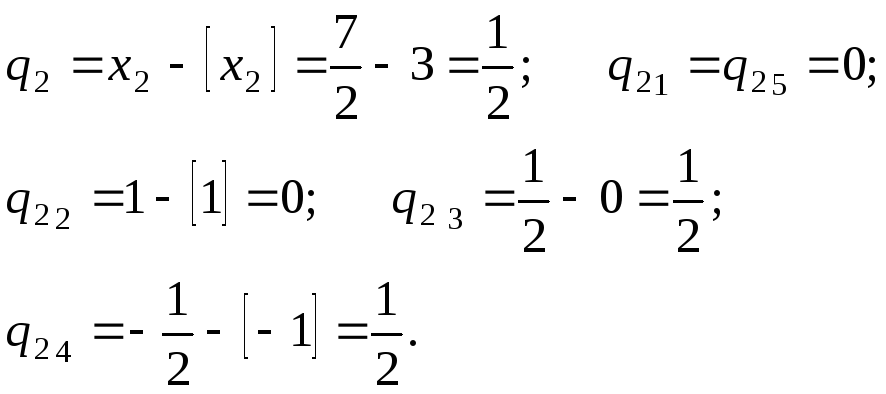
Таким образом, к системе ограничений задачи (5.5)-(5.7) добавляем неравенство

т. е.

(5.9)

Теперь находим максимальное значение функции (5.5) при выполнении условий (5.6), (5.7) и (5.9). В условие (5.9) вводим дополнительную переменную :

Таблица 5.5

Ввод в симплекс-таблицу дополнительной переменной

x1	x2	x3	x4	x5	x6
0 1 0 0	1 0 0 0	1/2 1/2 1 1	-1/2 1/2 2 1	0 0 1 0	0 0 0 -1	7/2 19/2 34 1
0	0	-5/2	-1/2	0	0	-71/2

Выберем . базис.

Таблица 5.6

Приведение симплекс-таблицы к базису

x1	x2	x3	x4	x5	x6
0 1 0 0	1 0 0 0	1 0 -1 1	0 0 0 1	0 0 1 0	-1/2 1/2 2 -1	4 9 32 1
0	0	-2	0	0	-1/2	-35

Базис ..

Запишем оптимальный план для исходной задачи: При этом плане значение целевой функции равно .

Геометрическая интерпретация решения задачи.

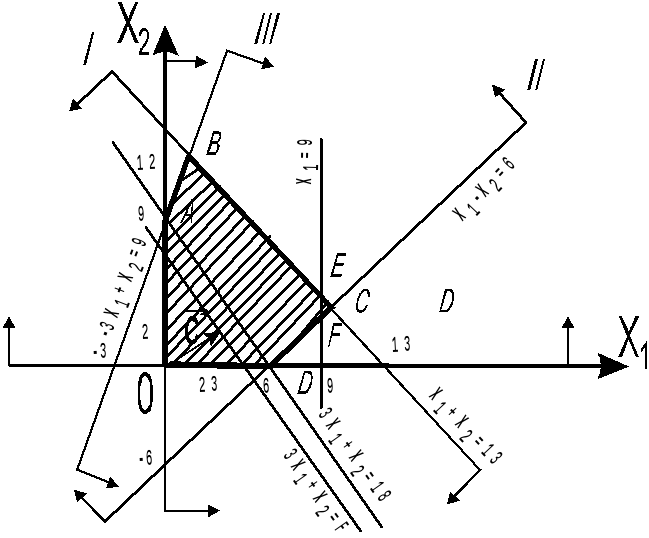
Рис.5.3. Геометрическая интерпретация решения задачи

Областью допустимых решений задачи (5.5)-(5.7) является многоугольник ОАВСD (рис. 5.3). Из рисунка видно, что максимальное значение целевая функция принимает в точке т.е.является оптимальным планом. Так как этот план не является оптимальным планом задачи (5.5)-(5.8) (числаи– дробные), то вводится дополнительное ограничение

Исключая из этого неравенства иподстановкой вместо них соответствующих значений из уравнений системы ограничений (5.6), получим.

.

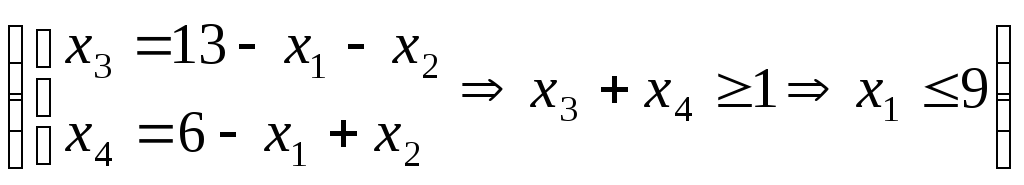Этому неравенству соответствует полуплоскость, ограниченная прямой отсекающей отмногоугольника ОАВСD треугольник EFC.

Как видно из рисунка, областью допустимых решений полученной задачи является многоугольник OABEFD. В точке E(9;4) этого многоугольника целевая функция данной задачи принимает максимальное значение. Так как координаты точки Е – целые числа и неизвестные ипринимают целочисленные значения при подстановке в уравнения (5.6) значенийитоявляется оптимальным планом задачи (5.5)-(5.8). Это следует и из таблицы симплекс-метода.

Замечание к использованию метода Гомори: если в первоначальный базис задачи входили искусственные векторы, то при составлении дополнительного ограничения искусственные переменные необходимо опустить.

Вопросы для самопроверки

1. Области применения целочисленного программирования.

2. Постановка задачи целочисленного программирования.

3. Графический способ решения задачи целочисленного программирования.

4. Алгоритм метода Гомори.

5. Правило составления дополнительного ограничения (сечения Гомори).

6. Геометрический смысл введения сечения Гомори.