Симплекс-метод решения задач линейного программирования

Рассмотрим задачу линейного программирования в канонической форме и на минимум целевой функции:

, ,,

(4.7)

где – вектора условий задачи, аВ – вектор ограничений этой задачи. Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме.

Допустимое решение задачи (4.7) в канонической форме называетсяопорным решением (планом) этой задачи, если векторы условий где– номера всех ненулевых координат образуют линейно независимую систему векторов.

Пример 4.3. Например, векторы иявляются допустимыми решениями задачи

Z=

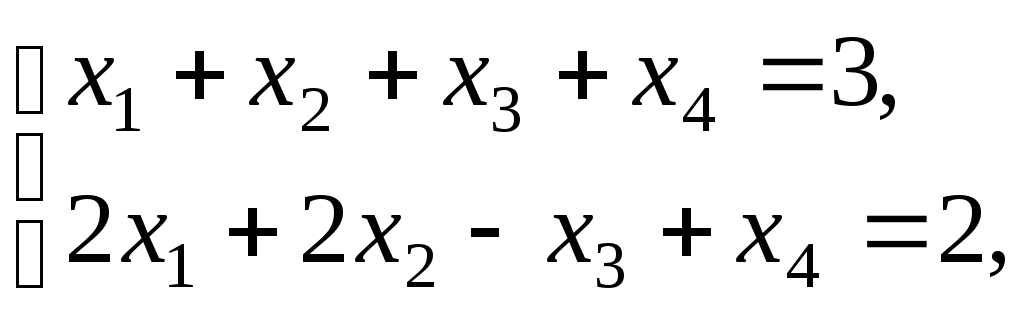
, 2, 3, 4.

Векторы условий 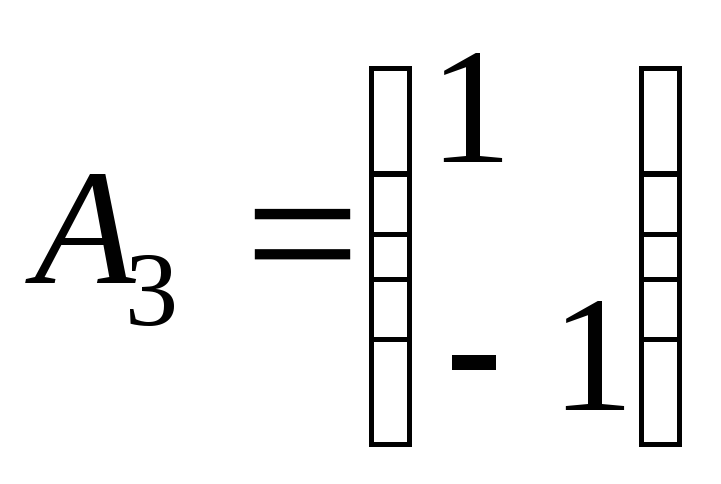,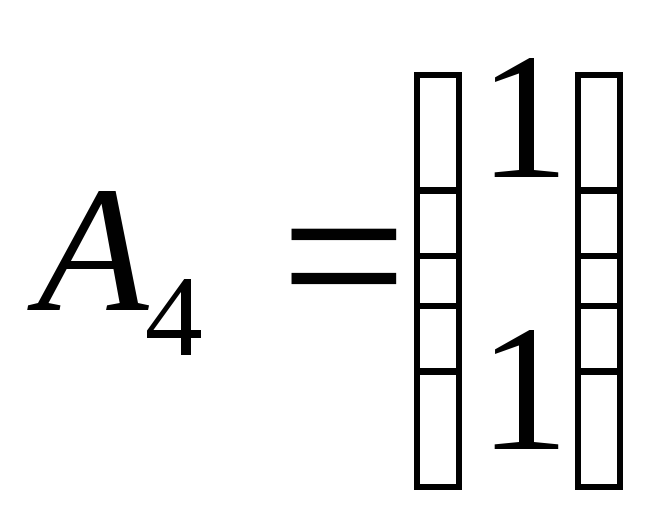образуют, очевидно, линейно независимую систему. Значит,является опорным решением данной задачи. Векторы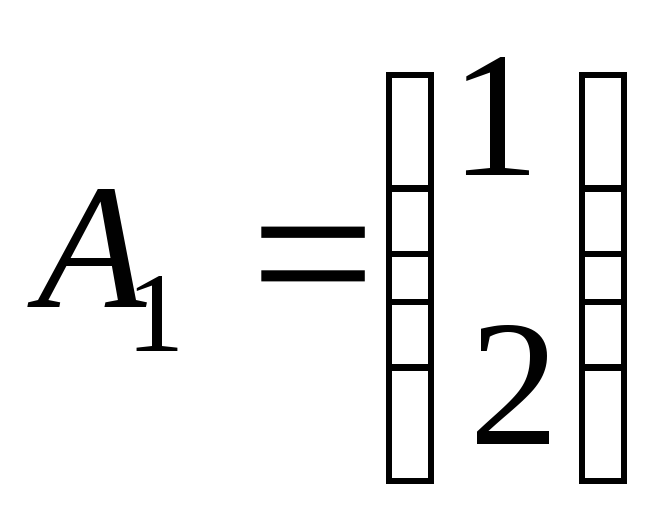,,линейно зависимы, поэтому₂ не является опорным решением.

Свойства опорных решений

1. Если допустимое множество задачи (4.7) в канонической форме не пусто, то эта задача имеет опорное решение.

2. Опорные решения задачи (4.7) являются крайними точками допустимого множества этой задачи. (Допустимое множество всегда выпукло.)

3. Задача (4.7) в канонической форме имеет лишь конечное число различных опорных решений (либо не имеет их вовсе).

Чтобы найти некоторое опорное решение задачи (4.7), достаточно выбрать базис системы векторов условий этой задачи так, чтобы вектор ограниченийВ раскладывался по нему с неотрицательными коэффициентами.

Если – такой базис итоявляется опорным решением задачи (4.7).

Базис системы векторов условийзадачи (4.7) называетсябазисом опорного решения этой задачи, еслипри.

Пример 4.4. Рассмотрим опорное решение задачи

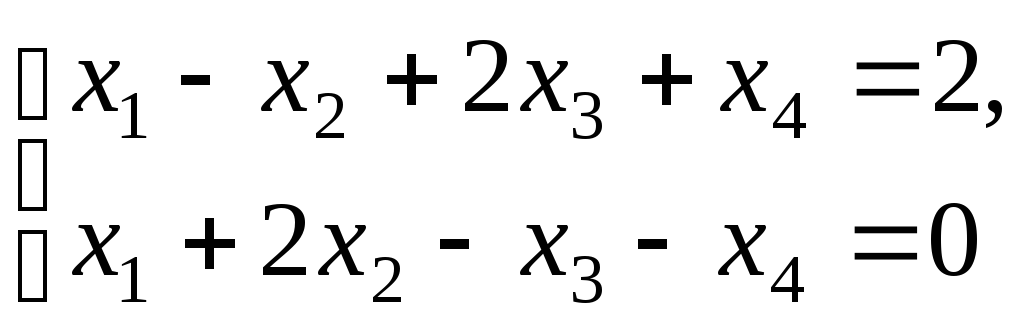
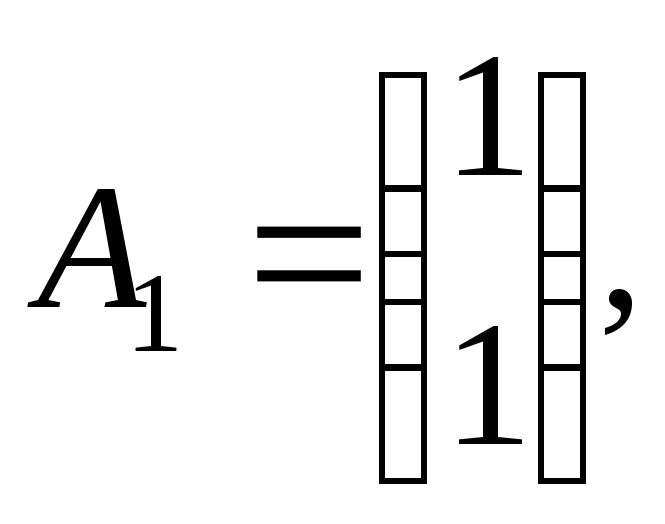
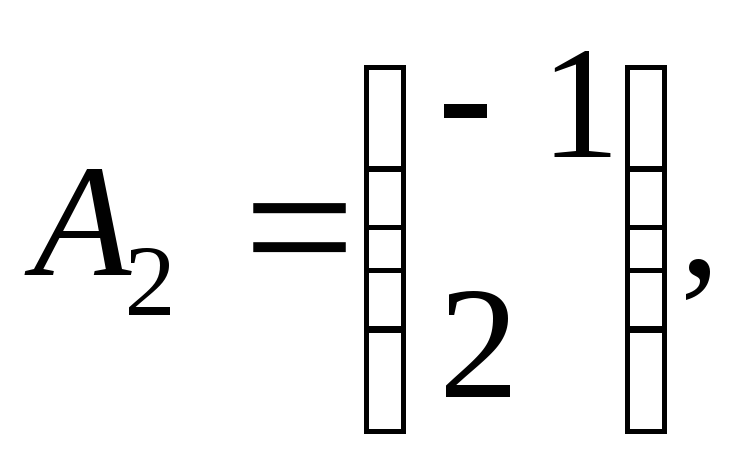
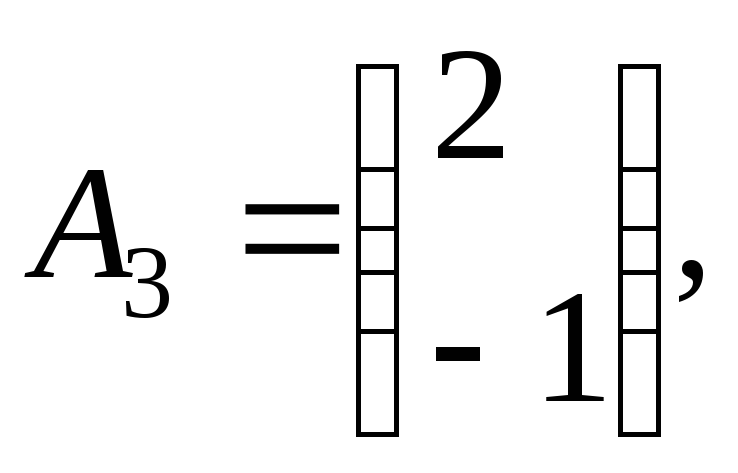
Здесь 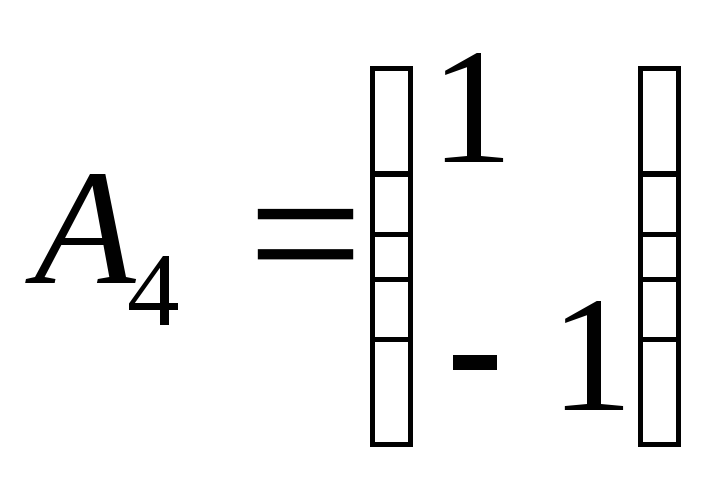ибазисы системы. Так как вторая и третья координаты вектораравны 0, тоявляется базисом опорного решения. С другой стороны, четвёртая координатаотлична от нуля. Следовательно,не будут базисом.

У любого опорного решения задачи (4.7) не может быть более, чем r ненулевых (положительных) координат, где r=rang(). Опорное решение называется невырожденным, если число его ненулевых координат точно равно r и вырожденным – в противном случае.

Любое опорное решение имеет базис, при этом у невырожденного опорного плана базис только один, а вырожденное опорное решение может иметь несколько различных базисов.

Опорные решения играют важную роль при решении задач линейного программирования в канонической форме, так как если задача имеет оптимальное решение, то одно из её опорных решений обязательно будет её оптимальным решением. Таким образом, оптимальное решение задачи линейного программирования в канонической форме можно искать только среди её опорных решений (а их лишь конечное число).

По задаче линейного программирования в канонической форме (4.7) всегда можно составить так называемую симплекс-таблицу:

Таблица 4.4

Исходная симплекс-таблица условий задачи линейного

программирования

х1	х2	...	...	хn
a11 a21 . . . am1	a12 a22 . . . am2	... ... ...	... ... ...	a1n a2n . . . amn	b1 b2 . . . bm
- c1	- c2	...	...	- cn	0

Предположим, что – некоторое опорное решение задачи (4.7), а векторыобразуют его базис. Тогда таблицу 4.4 можно преобразовать методом Гаусса в таблицу 4.5.

Прибавим к последней строке таблицы 4.5 первую строку, умножив на , вторую строку, умножив на,r-ю строку, умножив на . В результате получим новую таблицу 4.6, гдекоординаты опорного решения, соответствующие векторам базисагдеа(значению целевой функции на опорном решении).

Таблица 4.6, полученная указанным выше способом, называется симплекс-таблицей, приведённой к базису опорного решения, а числаоценками этого базиса.

Имеют место следующие утверждения (рассматривается случай задачи минимизации):

1. Если все оценки некоторого базиса опорного решения неположительны, то оно является оптимальным решением задачи линейного программирования в канонической форме (признак оптимальности).

Таблица 4.5

Приведённая к базису симплекс-таблица без изменений в последней строке

x1	...	xi1	...	xi2	...	xir	...	xs	...	xn
a'11 a'21 . . . a'k1 . . . a'r1		1 0 . . . 0 . . . 0		0 1 . . . 0 . . . 0		0 0 . . . 0 . . . 1		a'1s a'2s . . . a'ks . . . a'rs		a'1n a'2n . . . a'kn . . . a'rn	di1 di2 . . . dik . . . dir
- c1	...	- ci1	...	- ci2	...	- cir	...	- cs	...	- cn	0

Таблица 4.6

Приведённая к базису симплекс-таблица

x1	...	xi1	...	xi2	...	xir	...	xs	...	xn
a'11 a'21 . . . a'r1		1 0 . . . 0		0 1 . . . 0		0 0 . . . 1		a'1s a'2s . . . a'rs		a'1n a'2n . . . a'rn	di1 di2 . . . dir
1	...	i1	...	i2	...	ir	...	s	...	n	0

2. Для оптимального опорного решения задачи линейного программирования в канонической форме всегда существует базис, все оценки которого неположительны.

3. Предположим, что симплекс-таблица для задачи линейного программирования в канонической форме приведена к базису некоторого опорного решения. Если среди оценок этого базиса имеется положительная оценка , а все остальные элементыs-го столбца таблицы неположительны, то целевая функция не ограничена снизу на допустимом множестве. (Условие неограниченности нулевой функции – особый случай).

Пример 4.5. Рассмотрим опорное решение =(1;0;0;0) задачи:

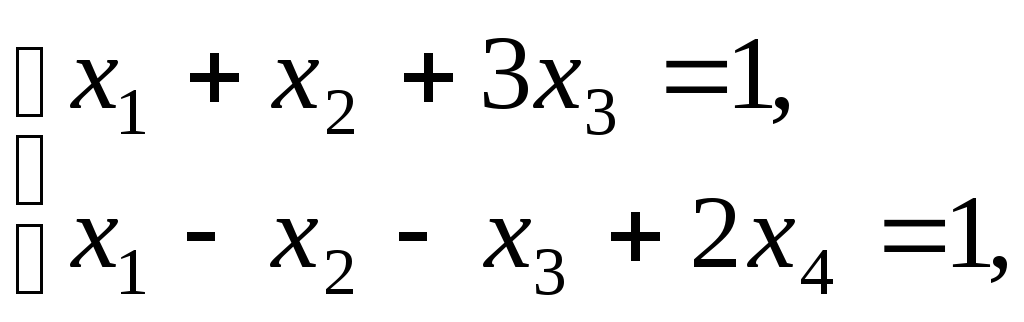
j = 1,2,3,4.

Приведём симплекс-таблицу для этой задачи к базису опорного решения.

Таблица 4.7

Ход преобразований по симплекс-методу для примера 4.5

x1	x2	x3	x4			x1	x2	x3	x4			x1	x2	x3	x4
1	1	3	0	1		1	1	3	0	1		1	0	1	1	1
1	-1	-1	2	1		0	-2	-4	2	0		0	1	2	-1	0
10	-1	9	-6	0		10	-1	9	-6	0		10	-1	9	-6	0

	x1	x2	x3	x4
	1	0	1	1	1
	0	1	2	-1	0
	0	0	1	-17	-10

Среди оценок базиса есть положительная оценка. Значит, утверждать на этом этапе, что– опорное решение, мы не можем.

С другой стороны, возьмем базис того же опорного решения. Приведя симплекс-таблицу к этому базису (таблица 4.8), получим, что все оценки базисанеположительны. Следовательно,оптимальное решение данной задачи.

Таблица 4.8

Приведённая к базису симплекс-таблица

x1	x2	x3	x4
1	-1/2	0	3/2	1
0	1/2	1	-1/2	0
0	-1/2	0	-33/2	-10