Тема 6 Транспортная задача

В настоящее время транспортная задача линейного программирования широко применяется как в теоретических разработках, так и в практике планирования различных экономических процессов. Особенно важное значение она имеет при решении вопросов рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта. Она применяется и при решении экономических проблем, которые по своему характеру не имеют ничего общего с транспортировкой груза, например, оптимальное закрепление за станками операций по обработке деталей ("станковая" задача), проблема выбора (оптимального назначения), задачи размещения производства с учётом транспортных и производственных затрат.

В общем виде постановка транспортной задачи такова. (Сейчас рассматривается классическая постановка задачи, её применение к станковой задаче рассмотрим позже).

Пусть некоторый однородный продукт, сосредоточенный у m поставщиков A_i в количестве a_i (i=1,2,…,m) единиц соответственно, необходимо доставить n потребителям B_j в количестве b_j () единиц. Известна стоимость c_ij перевозки единицы груза от i-го поставщика к j-му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребность и добиться минимальной стоимости перевозок.

Обозначим через x_ij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю; тогда условие задачи можно записать в виде таблицы, которую в дальнейшем будем называть матрицей планирования (табл. 6.1).

Таблица 6.1

Запись условий транспортной задачи

Поставщики	Потребители				Запасы
	B1	B2	...	Bn
A1	x11 С11	x12 C12	...	x1n C1n	A1
A2	x21 C21	x22 C22	...	x2n C2n	A2
...	...	...	...	...	...
Am	xm1 Cm1	xm2 Cm2	...	xmn Cmn	am
Потребности	b1	b2	…	bn	∑ai=∑bj

Составим математическую модель задачи. Так как от -го поставщика к-му потребителю запланировано к перевозкеединиц груза, то стоимость перевозки составит. Стоимость всего плана выразится двойной суммой.

Систему ограничений получаем из следующих условий задачи:

а) все грузы должны быть вывезены, т.е. ()(уравнения получаются из строк таблицы);

б) все потребности должны быть удовлетворены, т.е. () (уравнения получаются из столбцов таблицы).

Таким образом, математическая модель транспортной задачи имеет следующий вид:

Найти наименьшее значение линейной функции при ограничениях

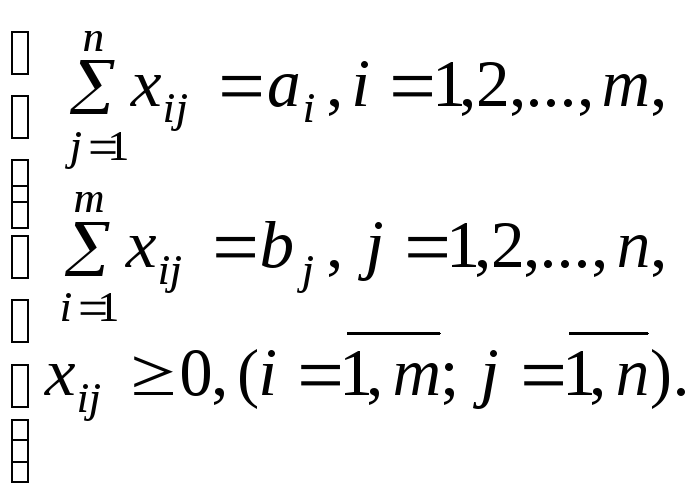
В рассмотренной модели может быть два случая: когда суммарные запасы равны суммарным потребностям, т.е. и когда не равны. В первом случае транспортная модель задачи называетсязакрытой, во втором – открытой.

Когда суммарные запасы не равны суммарным потребностям, может быть два случая:

а) суммарные запасы превышают суммарные потребности ;

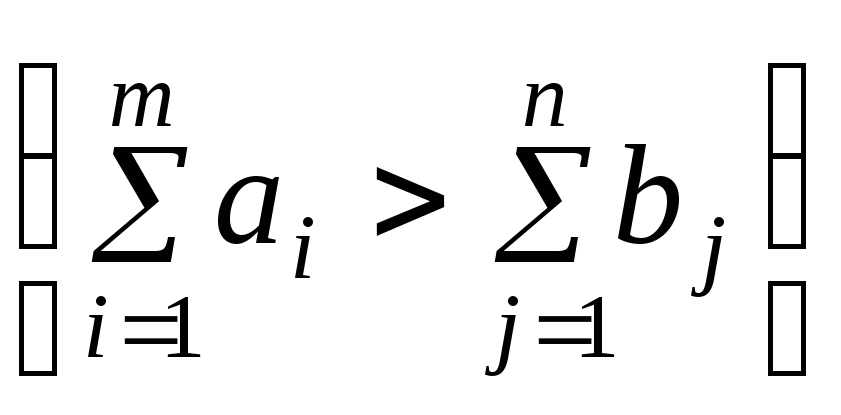б) суммарные потребности превышают суммарные запасы .

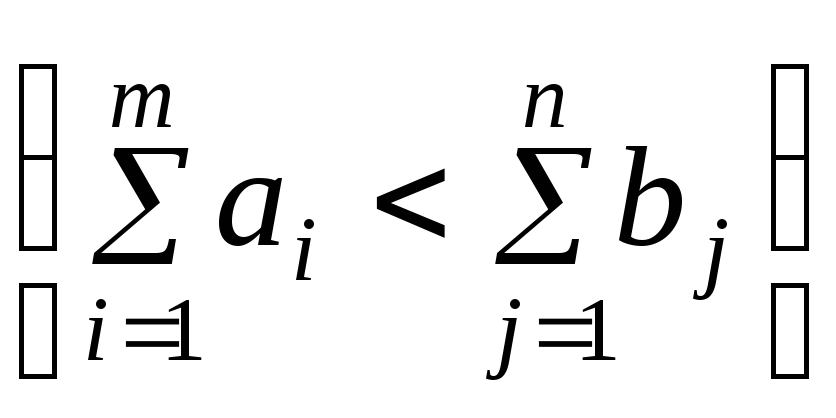Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.

В случае (а) ограничения имеют вид:

В случае (б) ограничения имеют вид:

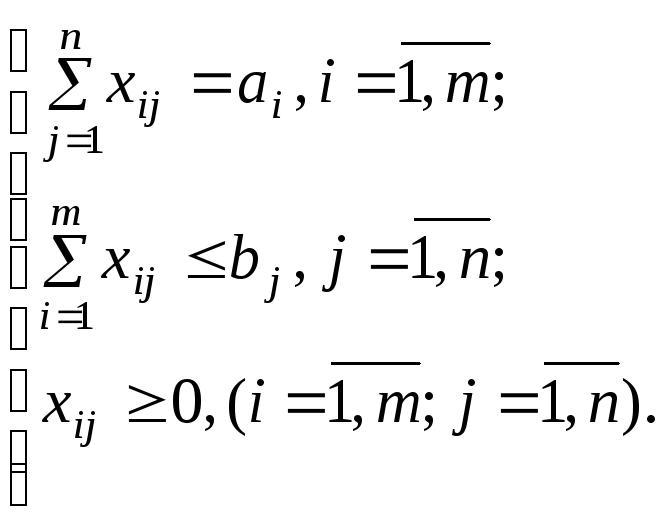
Открытая модель приводится к закрытой модели.

В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель потребности которогоВ случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщикзапасы которого

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными 0, т.к. в обоих случаях груз не перевозится. После преобразований задача принимает вид закрытой модели. Так что, прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверить, к какому виду модели она принадлежит, только после этого решать.

Существует следующая теорема.

Теорема 6.1. Любая транспортная задача, у которой суммарный объём запасов совпадает с суммарным объёмом потребностей, имеет решение.

Особенности транспортной задачи по сравнению с общей задачей линейного программирования вытекают из её математической модели: целевая функция имеет несколько другой вид (двойная сумма), вид коэффициентов специфический (там, где будет перевозка, коэффициент будет равен 1, в остальных - 0, т.е. в каждом столбце будет не более двух единиц, остальные элементы - нули). Методы решения транспортной задачи в силу этих особенностей отличны от методов решения задачи линейного программирования. Их мы рассмотрим позже.

Ранее представленная станковая задача полностью попадает под рассматриваемую модель транспортной задачи, если принять другой экономический смысл переменных. В самом деле, пусть на предприятии имеется m видов станков, максимальное время работы которых соответственно равно a_i (i=) часов. Каждый из станков может выполнять n видов операций. Суммарное время выполнения каждой операции соответственно равно b_j (j=) часов. Известна производительность c_ij i-го станка при выполнении j-й операции. Определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей.

Для составления математической модели обозначим через x_ij (i=,j=) время, которое i-й станок должен работать на j-й операции. Тогда количество деталей, обработанных на i-м станке, равно c_ijx_ij.. Количество деталей, обработанных на всех станках, можно выразить функцией .

Так как максимально возможное время работы i-го станка ограничено значением a_i, то получаем , (), если максимальное время работы станков используется полностью, или, если это время используется не полностью.

С другой стороны, время, отведённое на j-ю операцию, равно b_j часов, поэтому . Из условия следует, что общее время работы всех станков должно быть равно сумме максимальных времён работы всех станков, т.е., и времени, необходимому на выполнение всех операций, т.е.. Отсюда следует, что.

Таким образом, необходимо найти максимальное значение линейной функции при ограничениях

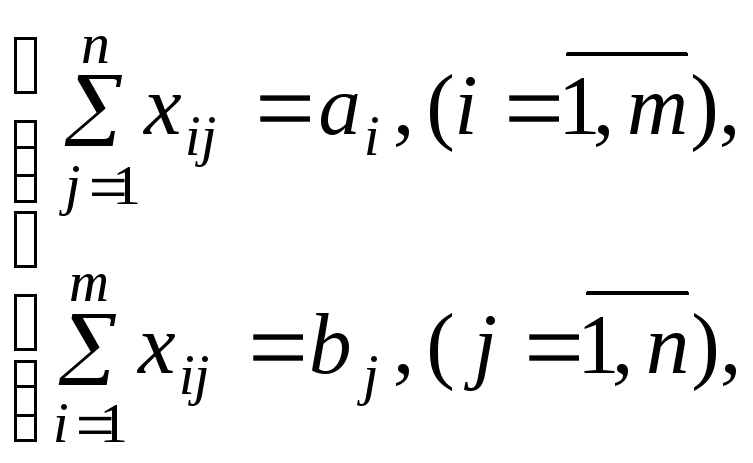
Для того чтобы решить эту задачу методом потенциалов, достаточно линейную функцию умножить на , т.е. считать в таблице матрицы планирования все значенияc_ij отрицательными (в канонической постановке транспортной задачи целевая функция должна быть на минимум).