Пример решения станковой задачи

Группа обо ру-дов.	Коли-чество ед. оборуд. в группе	Произ-водитель-ность ед. оборудо-вания		Первый вариант решения (на каждой группе изготавливают одинаковое количество изделий)		Оптимальный вариант решения (количество изделий, изготавливаемых по группам оборудования)		Оптимальный вариант решения (количество ед. оборудования, занятых изготовлением изделий)
		1-е изд.	2-е изд.	1-е изд.	2-е изд.	1-е Изд.	2-е изд.	1-е изд.	2-е изд.	Итого
I	3	10	20	20	20	26	6	8/3	1/3	3
II	3	20	30	36 (x=1,8)	36 (y=1,2)	60	-	3	-	3
III	1	30	80	21 (x=8/11)	21 (y=3/11)	-	80	-	1	1
Всего:				77	77	86	86	-	-	-

Решение этой системы линейных уравнений даёт х=2, а у=1, т.е. за первым изделием нужно закрепить 2 единицы, а за вторым – одну единицу оборудования первой группы. Суммарная производительность оборудования этой группы, соответствующая данному закреплению, и показана в таблице 4.1 в столбцах первого варианта решения.

Вычислим отношение производительностей по второму и первому изделиям для каждой группы оборудования и расположим их в порядке убывания (или возрастания) – 8/3(III), 2(I) и 3/2(II). Для группы, у которой это отношение имеет наибольшую величину, все единицы оборудования закрепим за вторым изделием, а у которой это отношение наименьшее – за первым. В оставшейся группе оборудование распределяется так, чтобы выровнять суммарное производство по изделию каждого вида. В данном примере это означает, что III группу оборудования, у которой отношение производительностей максимальное (8/3), нужно целиком закрепить за вторым изделием, а II группу с наименьшим отношением производительностей – за первым изделием. Группа I распределяется так, чтобы выровнять объём производства по обоим изделиям.

Для данного примера это выравнивание происходит путём решения системы двух линейных уравнений с двумя неизвестными.

Первое уравнение составляют так, чтобы количество первого и второго изделий, изготовляемое на всех группах оборудования, было одинаковым. В данном случае получим

10х+60=20у+80,

где х и у – количество единиц оборудования I группы, закреплённое соответственно за первым и вторым изделиями.

Второе уравнение составляется исходя из условия, что суммарное количество единиц оборудования I группы, закреплённое за первым и вторым изделиями, не должно превышать имеющегося количества, т.е. для данного случая х+у=3.

Найденное оптимальное решение позволяет увеличить выпуск изделий до 86, что по сравнению с первым возможным вариантом дает увеличение на 11,7% без каких-либо дополнительных затрат. Одновременно это приведёт и к снижению себестоимости изготовленных изделий.

Для задач большего объёма (с большим числом групп оборудования и видов изделий) найти решение значительно труднее и возможно лишь с использованием методов линейного программирования.

Запишем задачу в следующем виде:

максимизировать целевую функцию

L=10x₁₁+20x₂₁+30x₃₁→max

при условиях

где x_ij – количество единиц оборудования i-й группы, занятое изготовлением изделий j-го вида.

Если количество изделий каждого вида будет задано (что чаще практически и имеет место), то станковая задача может быть поставлена в другом виде. Вместо максимизации количества выпускаемых изделий в этом случае нужно найти минимум времени на производство всех изделий, т.е. минимум целевой функции

где х_ij – время, затрачиваемое i-й группой оборудования на изготовление изделий j-го вида;

а_ij – суммарная производительность всех единиц оборудования i-й группы в единицу времени при изготовлении изделий j-го вида;

N_j – заданное количество изделий j-го вида, которое требуется изготовить.

Так, если для рассматриваемого примера будет задано, что N₁=N₂=50, то задача запишется так:

минимизировать L=x₁₁+x₁₂ при условиях:

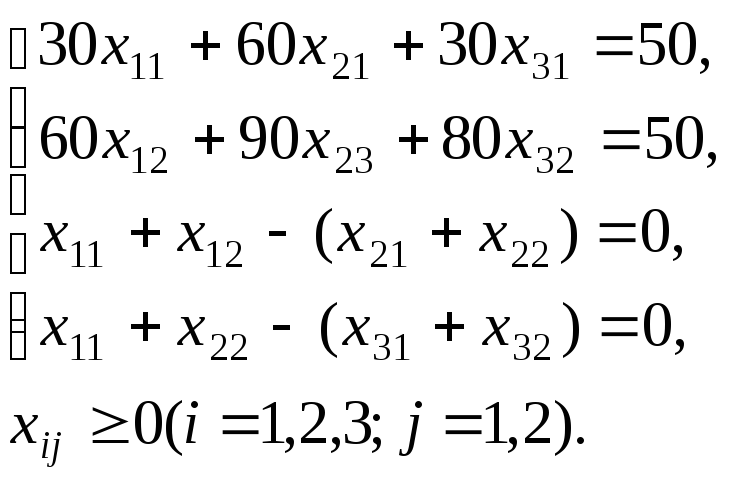
В такой задаче вместо групп оборудования могут быть взяты отдельные участки, цехи и предприятия в целом, если они выпускают одни и те же изделия. В этом случае задача ничем не будет отличаться от изложенной выше.

Для постановки и решения станковой задачи необходимо знать производительности или нормы времени на изготовление изделий по каждой группе оборудования, т.е. иметь нормы времени для всех технологических процессов, по которым будут изготавливаться эти изделия. На практике же это бывает очень редко.

Эта задача в несколько изменённом виде используется также при распределении производственной программы между предприятиями, точнее, при решении задач по размещению и концентрации производства.

Задача оптимального раскроя материала (задача по раскрою) является одним из частных случаев задачи по оптимальному использованию комплексного сырья.

Математическую модель задачи оптимального использования сырья можно представить в следующем виде.

Пусть выпускается n видов продукции, используется m видов сырья. Обозначим через S_i (i=1,…,m) виды сырья; b_i – запасы сырья i-го вида; P_j (j=1,…,n) – виды продукции; a_ij – количество единиц i-го сырья, идущего на изготовление единицы j-й продукции; с_i – величину прибыли, получаемой при реализации единицы j-й продукции.

Условия задачи запишем в таблице 4.2.

Пусть x_ij – количество единиц j-й продукции, которое необходимо произвести. Сама модель:

найти максимальное значение линейной функции

Z=c₁x₁+ +c₂x₂+…+c_nx_n

при ограничениях

,

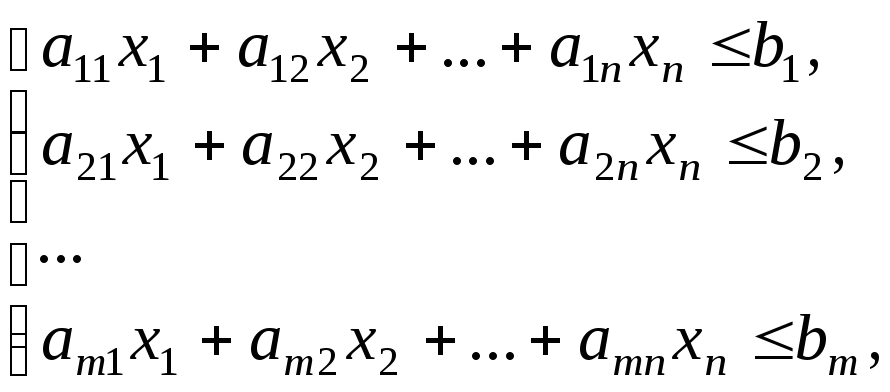
где a_ij – количество сырья, расходуемое на изготовление единицы продукции, b_i – общее количество сырья i-го вида, c_j – величина прибыли, получаемой с единицы j-й продукции.

Система ограничений и функция цели составляют математическую модель рассматриваемой экономической задачи.

Как мы уже выясняли, допустимым решением (или планом) задачи линейного программирования является совокупность чисел х=(х₁,х₂,…,х_n), удовлетворяющих ограничениям задачи. План х^*=(х₁^*,х₂^*,…,х_n^*), при котором целевая функция задачи принимает своё максимальное (минимальное) значение, называется оптимальным.

Таблица 4.2

Условия задачи оптимального использования комплексного сырья

Виды	Запасы	Количество единиц i-го сырья, идущего на изготовление единицы j-й продукции
сырья	сырья	P1	P2	...	Pn
S1	b1	a11	a12	...	a1n
S2	b2	a21	a22	...	a2n
...	...	...	...	...	...
Sm	bm	am1	am2	...	amn
Прибыль		с1	с2	...	сn

Форма записи задачи линейного программирования может быть различной. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения целевой функции при выполнении условий в виде системы неравенств и неотрицательности переменных. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении минимального значения целевой функции при выполнении условий в виде системы линейных уравнений и неотрицательности переменных. В общей задаче линейного программирования могут быть условия, как в виде системы неравенств, так и в виде равенств, причем не на все переменные может быть наложено условие неотрицательности:

.

Указанные выше три формы записи задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Для этого необходимо уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений – неравенств к ограничениям – равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти функцию L=c₁x₁+c₂x₂+…+c_nx_n, можно перейти к нахождению максимума функции L₁= -L= -c₁x₁-c₂x₂-… -c_nx_n, поскольку min L₁= -max(-L).

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид "≤", преобразовать в ограничение- равенство можно добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида "≥" – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

a_i1x₁+a_i2x₂+…+a_inx_n≤b_i

преобразуется в ограничение-равенство

a_i1x₁+a_i2x₂+…+a_inx_n+x_n+1=b_i (x_n+1≥0),

а ограничение-неравенство

a_i1x₁+a_i2x₂+…+a_inx_n≥b_i

• в ограничение-равенство

a_i1x₁+a_i2x₂+…+a_inx_n-x_n+1=b_i (x_n+1≥0).

В то же время каждое уравнение системы ограничений может быть представлено так:

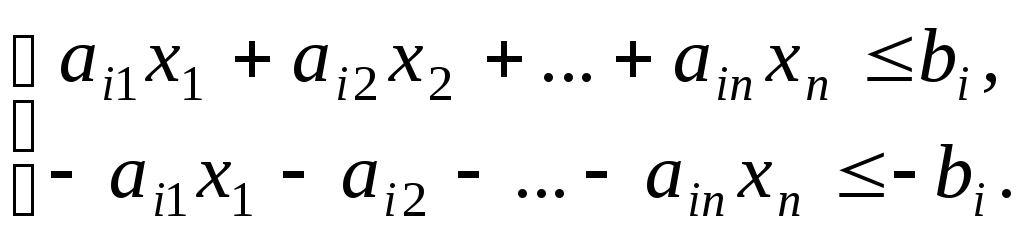
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определённый экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объёму неиспользованного соответствующего ресурса.

Отметим, наконец, что если переменная х_k не подчинена условию неотрицательности, то её следует заменить двумя неотрицательными переменными u_k и v_k, приняв x_k=u_k-v_k.

Рассмотрим каноническую задачу линейного программирования. Перепишем её в векторной форме: найти минимум функции L=CX при условиях A₁x₁+A₂x₂+…+A_nx_n=B, (*)

где C=(с₁;с₂;…;с_n), X=(х₁;х₂;…;х_n); CX – скалярное произведение векторов; А₁,…,А_n и В – m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы уравнений задачи:

.

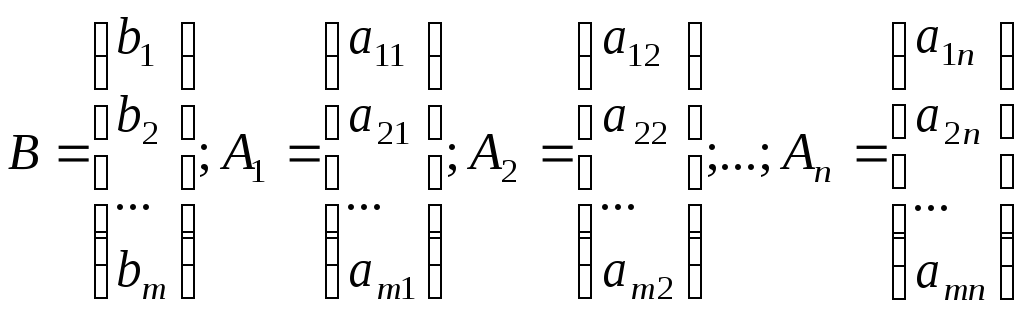Определение 4.1. План X=(х₁;х₂;…х_n) называется опорным планом канонической задачи линейного программирования, если система векторов A_j, входящих в разложение (*) с положительными коэффициентами, линейно независима.

Так как векторы A_j являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем m.

Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае он называется вырожденным.

Свойства канонической задачи линейного программирования тесным образом связаны со свойствами выпуклых множеств.

Теорема 4.1. Множество планов канонической задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов канонической задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.

Теорема 4.2. Если каноническая задача линейного программирования имеет оптимальный план, то максимальное (минимальное) значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное (минимальное) значение целевая функция задачи принимает более, чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией его вершин.

Теорема 4.3. Если система векторов А₁,А₂,…,А_k (k≤n) в разложении (*) линейно независима и такова, что А₁х₁+А₂х₂+…+А_kx_k=B, где все x_j≥0, то точка X=(х₁;х₂;…;х_k;0;…;0) является вершиной многогранника решений.

Теорема 4.4. Если X=(х₁;х₂;…х_n) – вершина многогранника решений, то вектора A_j, соответствующие положительным x_j в разложении (*), линейно независимы.

Сформулированные теоремы позволяют сделать следующие выводы.

Непустое множество планов канонической задачи линейного программирования образуют выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т.е. для одного из опорных планов) значение целевой функции является максимальным (минимальным) при условии, что функция ограничена сверху (снизу) на множестве планов. Если экстремальное значение функции принимает значение более, чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин, т. е. на отрезке.

Вершину многогранника решений, в которой целевая функция принимает экстремальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более 2-х переменных или задача, записанная в форме канонической, содержит не более 2-х свободных переменных, т.е. n-r≤2, где n – число переменных, r – ранг матрицы, составленной из коэффициентов в системе ограничений задачи.

Найдём решение задачи (записанной в форме стандартной), состоящей в определении максимального значения функции L=c₁x₁+c₂x₂ при условиях

a_i1x₁+ +a_i2x₂≤b_i (i=1,…,k),

x_j≥0 (j=1,2).

Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость с граничными прямыми a_i1x₁+a_i2x₂=b_i (i=1,…,k), х₁=0 и х₂=0. В том случае, если система неравенств совместна, область её решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей выпуклое, то областью допустимых решений задачи является выпуклое множество, которое называется многоугольником решений (многогранником, когда n≥3). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.

Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция L принимает максимальное значение (для стандартной задачи линейного программирования). Эта точка существует тогда, когда многоугольник решений не пуст, и на нём целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня с₁х₁+с₂х₂=h (где h – некоторая постоянная), проходящую через многоугольник решений, и будем передвигать её в направлении вектора =(с₁;с₂) до тех пор, пока она не пройдёт через последнюю её общую точку с многоугольником решений. Координаты указанной точки и определят оптимальный план данной задачи.

Заканчивая рассмотрение геометрической интерпретации задачи линейного программирования, отметим, что при нахождении её решения могут встретиться случаи, изображённые на рис. 4.1-4.4. Рис. 4.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке A.

Из рис. 4.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка AB. На рис. 4.3 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рис. 4.4 – случай, когда система ограничений задачи несовместна. Последние 3 случая – это особые случаи.

Рис.4.1. Случай 1

Рис. 4.2. Случай 2

Рис.4.3. Случай 3

Рис.4.4. Случай 4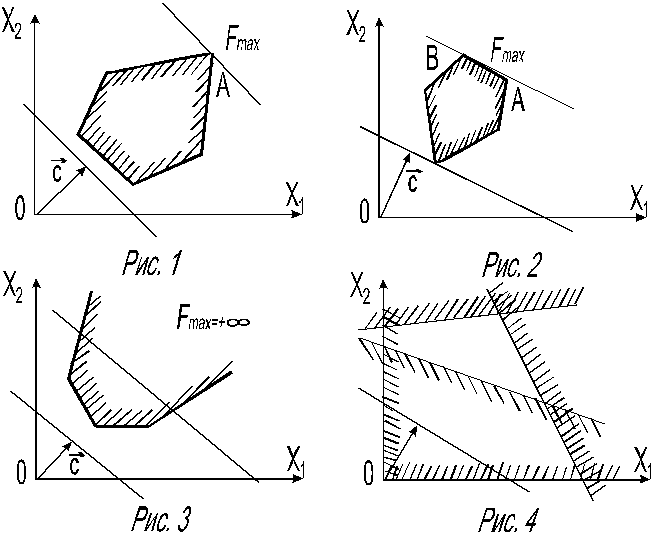

Отметим, что нахождение минимального значения линейной целевой функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня с₁х₁+с₂х₂=h передвигается не в направлении вектора =(с₁;с₂), а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении её минимального значения.

Итак, нахождение решения задачи линейного программирования на основе её геометрической интерпретации включает следующие этапы:

1. Строят прямые, уравнения которых получают в результате замены в ограничениях знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определяемые каждым из ограничений задачи.

3. Находят многоугольник решений.

4. Строят вектор =(с₁;с₂).

5. Строят прямую с₁х₁+с₂х₂=h, проходящую через многоугольник решений.

6. Передвигают прямую с₁х₁+с₂х₂=h в направлении вектора , в результате чего-либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.

7. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

Рассмотрим пример.

Пример 4.1. Для производства двух видов изделий А и В предприятие использует три вида сырья. Норма расхода сырья каждого вида на изготовление единицы продукции данного вида приведена в таблице. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.

Таблица 4.3

Условия задачи оптимального использования сырья

Вид сырья	Нормы расхода сырья (кг) на одно изделие		Общее количество
	A	B	сырья (кг)
I II III	12 4 3	4 4 12	300 120 252
Прибыль от реализации одного изделия (руб.)	30	40

Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.

Решение. Предположим, что предприятие изготовит изделий видаА и изделий видаВ. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьём каждого вида, и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства:

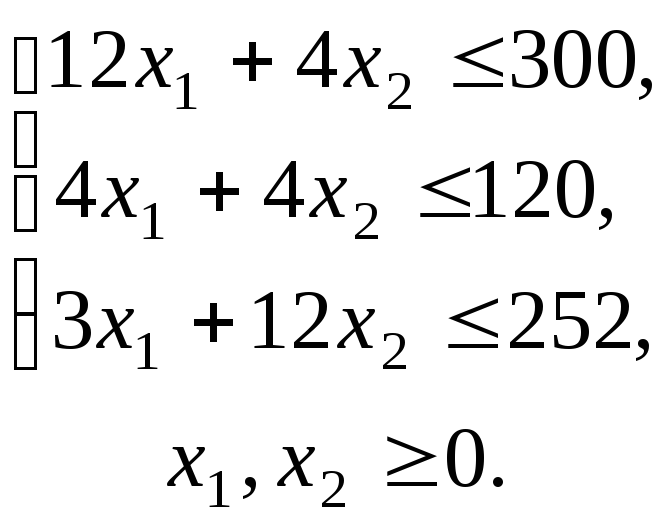
Общая прибыль от реализации изделий вида А и изделий видаВ составит F=30+ 40.

Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.

Решим сформулированную задачу геометрическим способом. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдём соответствующие прямые:

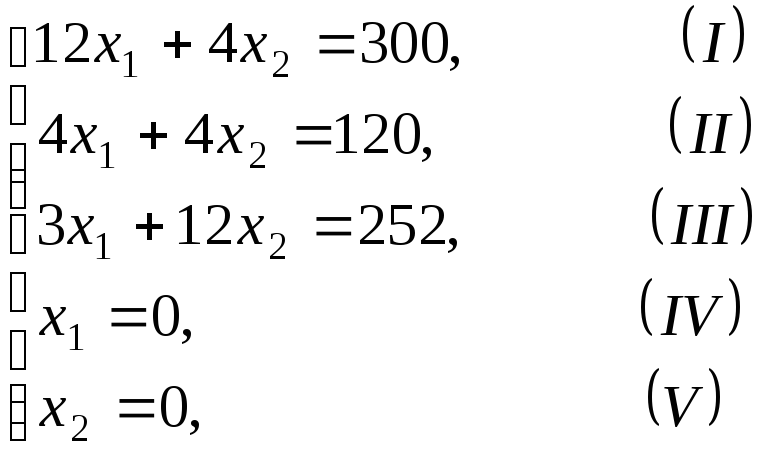
Эти прямые изображены на рис. 4.5. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли её координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.

Найдем, например, полуплоскость, определяемую неравенством 12+4<300. Для этого, построив прямую 12+4=300 (пр.I), возьмём какую-нибудь точку, принадлежащую одной из полученных полуплоскостей, например, точку O(0;0). Координаты этой точки удовлетворяют неравенству: 12, значит, полуплоскость, которой принадлежит точкаO(0;0), определится неравенством 12.

Это и показано стрелками на рис. 4.5.

Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.

Как видно из рисунка, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных.

Рис.4.5. Геометрический метод решения примера 4.1

Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение. Чтобы найти указанную точку, построим вектор и прямую 30, гдеh – некоторая постоянная такая, что прямая 30имеет общие точки с многоугольником решений. Положим, например, h=480 и построим прямую 30(рис. 4.5). Точки пересечения с осями.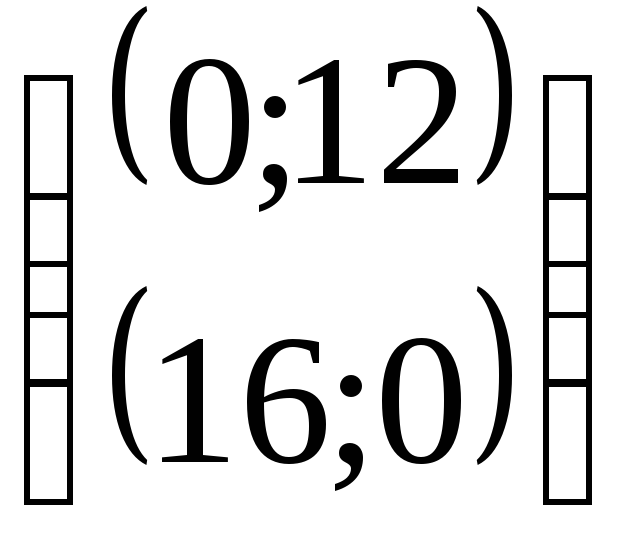

Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то её координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют план производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб.

Перемещая построенную прямую 30в направлении вектора, видим, что последней общей точкой её с многоугольником решений задачи служит точкаВ. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.

Найдем координаты точки В как точки пересечения прямых II и III. Следовательно, её координаты удовлетворяют уравнениям этих прямых:

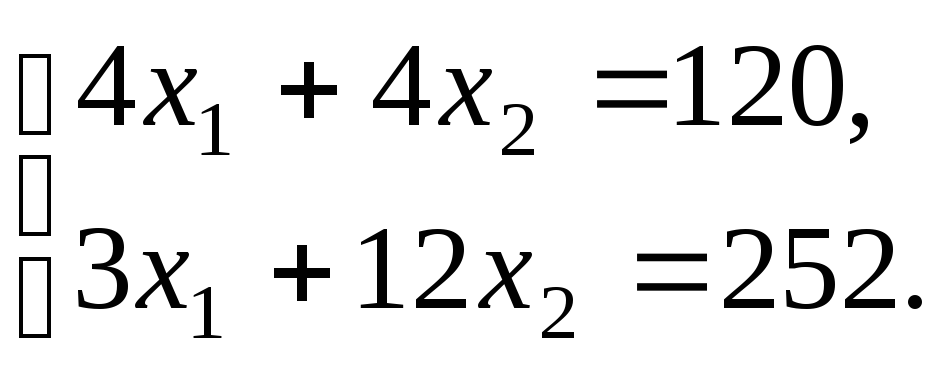
Решив эту систему уравнений, получим =12,=18. Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную =руб.

Вообще, с помощью графического метода может быть решена такая задача линейного программирования, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если n и m связаны соотношением n-m=2.

Действительно, пусть поставлена каноническая задача линейного программирования: найти минимальное значение линейной функции Z= при ограничениях

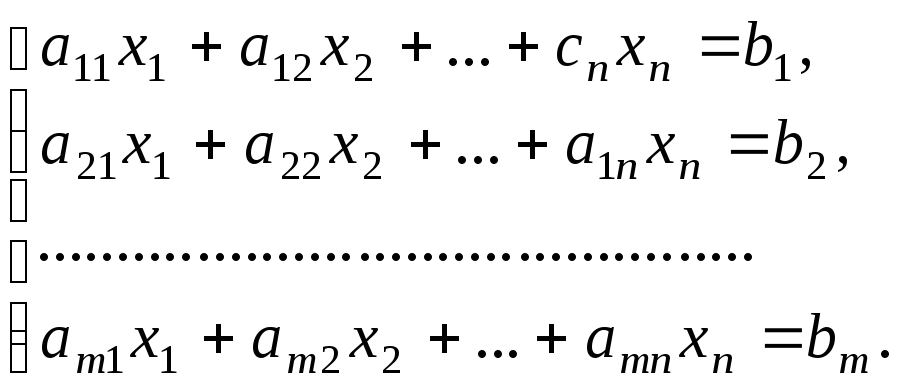
где все уравнения линейно независимы и выполняется соотношение n-m=2.

Используя метод Гаусса, производим m исключений, в результате которых базисными неизвестными оказались, например, m первых неизвестных , а свободными – два последних и , т.е. система ограничений приняла вид:

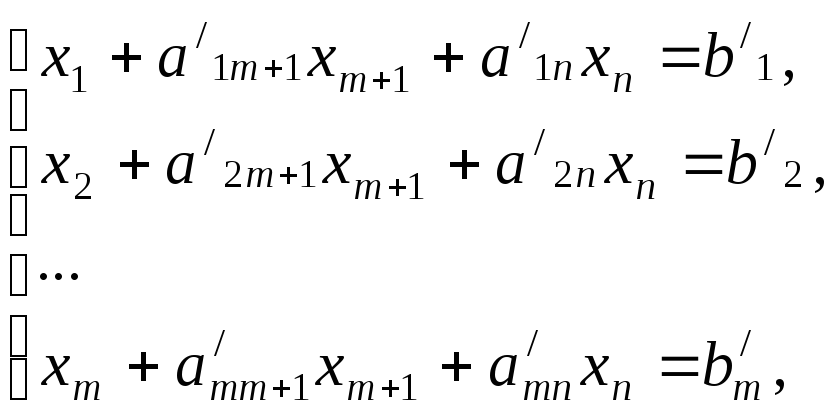(4.4)

(j=1,2,…,n).

С помощью уравнений преобразованной системы выражаем линейную функцию только через свободные неизвестные и, учитывая, что все базисные переменные - неотрицательные (,j=1,2,…,n), отбрасываем их, переходя к системе ограничений, выраженных в виде неравенств. Таким образом, окончательно получаем следующую задачу:

Найти минимальное значение линейной функции Z= при ограничениях

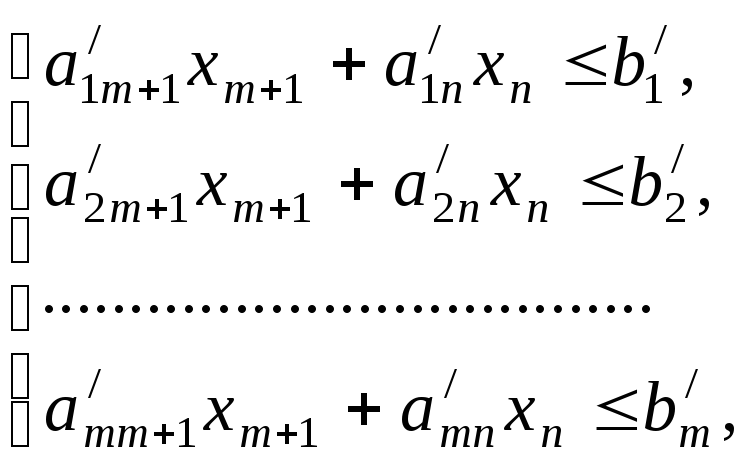
Преобразованная задача содержит две неизвестных; решая её геометрическим способом, находим оптимальные значения и, а затем, подставляя их в (4.4), находим оптимальные значения.

Пример 4.2. Геометрическим способом найти оптимальный план задачи линейного программирования, при котором линейная функция достигает максимального значения при ограничениях

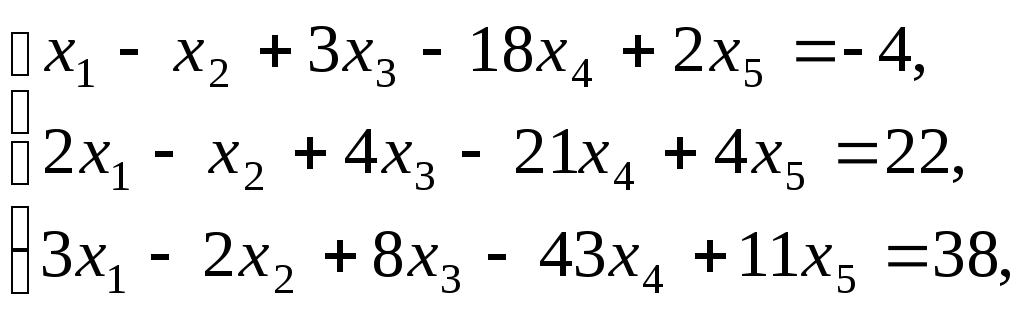(4.5)

Решение. Используя метод Гаусса, произведём три полных исключения . В результате приходим к системе

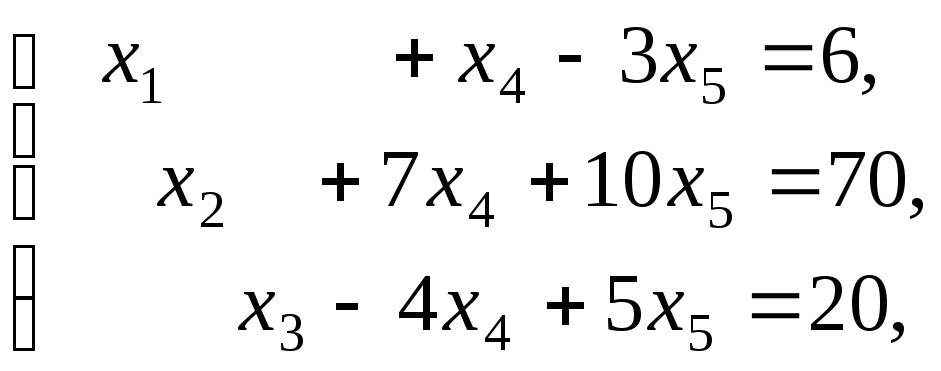откуда

(4.6)

Подставляя эти значения в целевую линейную функцию и отбрасывая в системе (4.5) базисные переменные, получаем задачу, выраженную только через свободные неизвестные и :

найти максимальное значение линейной функции при ограничениях

(подставлены значения из (4.6)).

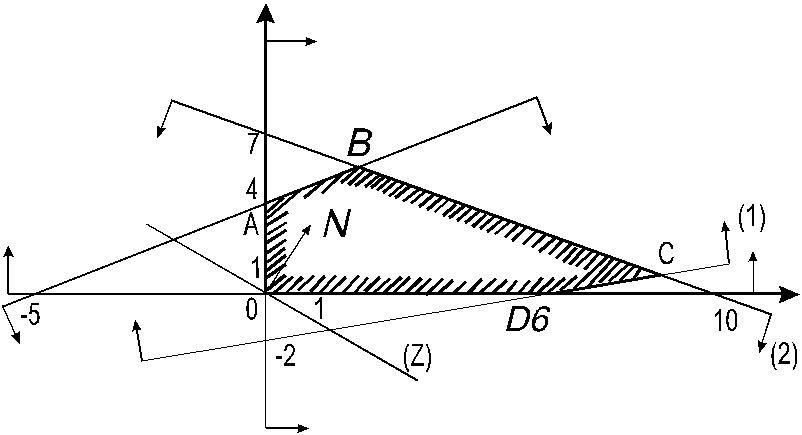
Рис.4.6. Геометрический метод решения примера 4.2

Построим многоугольник решений и линейную функцию в системе координат O (рис. 4.6). Из рисунка заключаем, что линейная функция принимает максимальное значение в угловой точке В, которая лежит на пересечении прямых 2 и 3. В результате решения системы

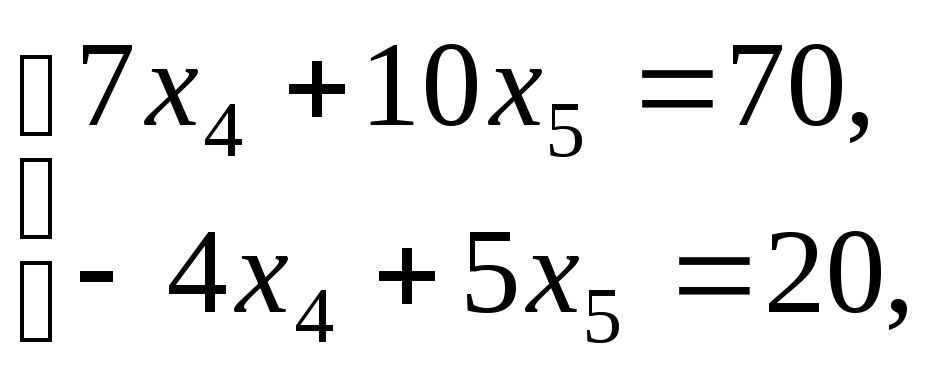находим: ,.

Максимальное значение функции -38+12+84=58. Для отыскания оптимального плана исходной задачи подставляем в (4.6) найденные значения и. Окончательно получим:; ; ;; .