3.3. Частотные характеристики параллельного колебательного контура

 

Простейший параллельный колебательный контур с потерями в ветвях R ₁и R₂ имеет вид, изображенный на рис. 4.13. Комплекс­ная входная проводимость такого контура

Из уравнения (4.56) следует, что резонанс в параллельном кон­туре возможен лишь в случае неотрицательности подкоренного вы­ражения (т. е. при R₁ < ρ и R₂< ρ или R₁> ρ и R₂ > ρ).

Реактивные составляющие токов в ветвях при резонансе равны друг другу:

При этом ток в неразветвленной части цепи определяется из уравнения

где активное сопротивление Яоэ, называют эквивалентным резо­нансным сопротивлением параллельного контура. Как следует из уравнения (4.58), входной ток контура совпадает по фазе с при­ложенным напряжением. Величину R₀₃ МОЖНО найти из условия резонанса токов. Так как при резонансе токов В = 0, то согласно (4.53) и (4.54) полная эквивалентная проводимость контура

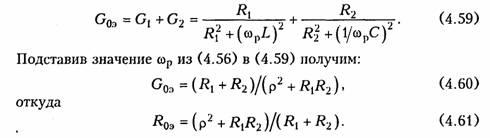
Наибольший теоретический и практический интерес представ­ляют резонанс токов в контурах без потерь и с малыми потерями.

Контур без потерь. Для контура без потерь (R₁= R₂ = 0) урав­нение резонансной частоты (4.56) принимает вид

т. е. совпадает с выражением (4.21) для последовательного кон­тура. Эквивалентное сопротивление контура без потерь R_0Э = ∞ и входной ток равен нулю, а добротность обращается в бесконеч­ность. Комплексы действующих значений токов в ветвях

т. е. ток в индуктивности отстает от приложенного напряжения на π/2, а в емкости опережает на π/2. На рис. 4.14, а изображена векторная диаграмма токов для этого случая при U = Ue^]0 = U.

Сумма энергий электрического и магнитного полей для парал­лельного контура без потерь, как и для последовательного контура

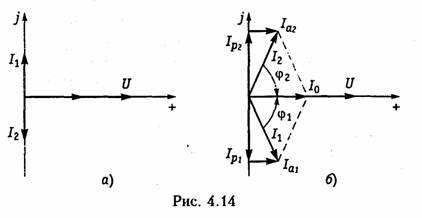
остается неизменной, т. е. энергетические процессы протекают ана­логично процессам в последовательном контуре.

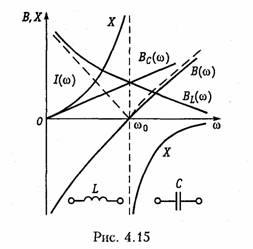
Частотные  зависимости  характеристик  параллельного  контура от частоты имеют вид

т. е. является зеркальным отображением модуля реактивной про­водимости |В(ω)| (на рис. 4.15 показано штриховой линией).

Контур с малыми потерями  Резонансная частота для этого случая будет приближенно совпадать с частотой шо. Для контура с малыми потерями можно принять, что ρ>> R₁ R₂, тогда

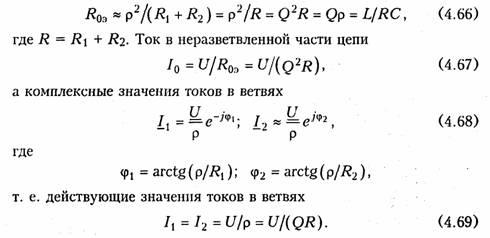
Из уравнений (4.67) и (4.69) следует, что отношение токов в ветвях к току в неразветвленной части цепи равно добротности контура:

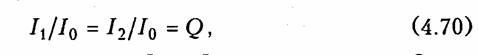
т. е. ток в реактивных элементах L и С при резонансе в Q раз больше тока на входе контура (отсюда термин «резонанс токов»). На рис. 4.14, б изображена векторная диаграмма токов для этого

 

 

 

случая. В контуре с потерями сумма энергий электрического и магнитного полей не остается постоянной с течением времени.

Интересен случай R₁ = R2 = ρ. Как; следует из уравнения (4.56), для ω_р получаем неопределенность, при этом входное со­противление контура имеет чисто резистивный характер на любой частоте (случай безразличного резонанса).

Рассмотрим частотные характеристики контура с малыми поте­рями. Комплексное эквивалентное сопротивление контура можно определить уравнением

На рис. 4.16, а изображены нормированные относительно i?₀» частотные характеристики R_a/Ro_Э, X_Э/Ro_Э, и Z_Э/Ro_Э как функции обобщенной расстройки ζ. Фазочастотная характеристика цепи оп ределится уравнением (рис. 4.16. б):

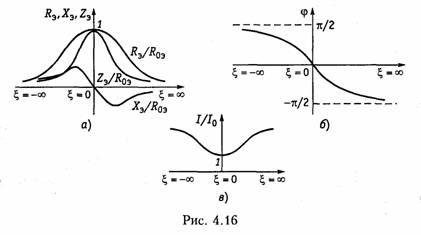
Анализ полученных зависимостей показывает, что по своему виду частотные характеристики контура с потерями существенно отличаются от характеристик контура без потерь. Это отличие касается прежде всего зависимости реактивного сопротивления кон­тура от частоты: для контура с потерями при резонансе оно ока­зывается равным нулю (см. рис. 4.16, а), а в контуре без потерь терпит разрыв (см. рис. 4.15).

Зависимость комплексного входного тока от частоты определя­ется из уравнения

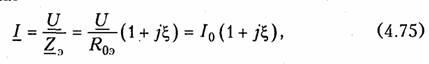
т. е. при резонансе (ζ = 0) ток принимает минимальное значение, определяемое формулой (4.58) (рис. 4.16, в).

Частотная зависимость токов I₁(ω) и I₂(ω) в ветвях определя­ется согласно закону Ома:

Сравнение формул (4.32) —(4.38) с формулами (4.78) —(4.81) показывает, что КПФ по току параллельного контура дуально соответствует КПФ по напряжению для последовательного кон­тура.

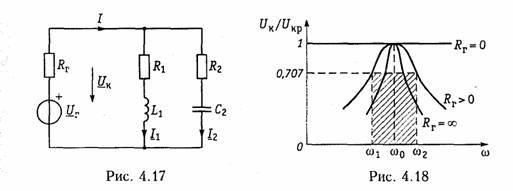
Рассмотрим, как влияет на резонансные свойства параллельного контура подключение его к источнику с задающим напряжением U_r внутренним сопротивлением R_r. При этом выходное на­пряжение снимается с контура (рис. 4.17). Нетрудно видеть, что комплексное напряжение на контуре

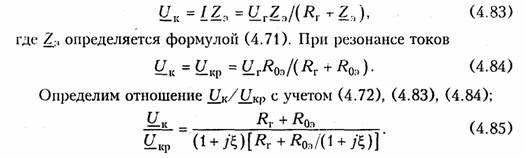
На рис. 4.18 показан характер этих зависимостей при различ­ных сопротивлениях R_r источника.

Полоса пропускания параллельного контура определяется как полоса частот, на границе которой напряжение на контуре умень­шается в √2 раз относительно U_Kp (см. рис. 4.18):

Сравнение уравнении (4.50) с уравнениями (4.91) и (4.92) показы­вает, что параллельный контур в общем случае имеет более широкую полосу пропускания, чем последовательный с такой же добротностью. И только при R_r =∞ (см. рис. 4.18) их полосы пропускания равны.

Таким образом, для улучшения избирательных свойств парал­лельного контура его необходимо возбуждать источником тока. Из уравнения (4.84) также следует, что параллельный контур нельзя использовать для усиления напряжения, если использовать незави­симый источник, так как при этом U_Kp < U_r.

Поэтому для усиления напряжения и получения высокой доб­ротности параллельного контура используют активные цепи с зави­симыми источниками тока. На рис. 4.19 приведен пример подобной схемы на базе полевого транзистора и его эквивалентная схема за­мещения.