2.5. Гармонические колебания в цепи при параллельном соединении r, l, с-элементов

Приложим к цепи, содержащей параллельно соединенные эле­менты R, L, С (рис. 3.10), напряжение

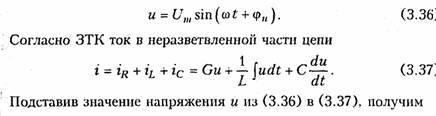
На рис. 3.11 изображена векторная диаграмма токов, описываемых уравнением (3.39).

Ток в резистивном сопротивлении I_тR называют активной со­ставляющей тока I_та, а разность тока I_тр = I_тL — 1_тс — реак­тивной составляющей тока. Для I_тa и I_тр справедливы соотно­шения

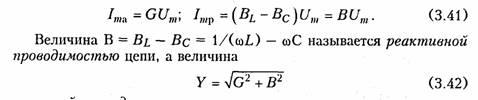
— полной проводимостью цепи.

По аналогии с треугольником напряжений и сопротивлений при параллельном соединении элементов можно ввести треугольники токов и проводимостей (рис. 3.12, а, б). Как следует из этих ри-

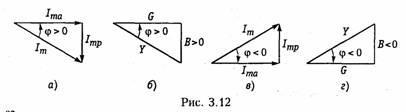
сунков, при I_тL > ImC (B_L > B_C) цепь носит индуктивный характер (общий ток отстает от приложенного напряжения) и при I_тL < I_mc (B_L < B_C) — емкостный характер (ток опережает приложенное на­пряжение). Из треугольников токов и проводимостей следует:

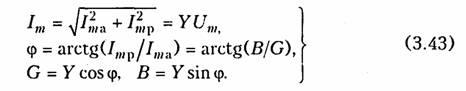
Сравнение треугольников токов и проводимостей с треугольни­ками напряжений и сопротивлений показывает их дуальный ха­рактер. Дуальны также и все соотношения, описывающие цепи при последовательном и параллельном соединении элементов, дуальны и сами цепи.

 

2.6. Символический метод расчета разветвленных цепей

 

Расчет разветвленных цепей при смешанном соединении элементов в режиме гармонических колебаний обычно осуществляется символическим методом. Это объясняется тем, что классический метод расчета приводит к громоздким интегрально-дифферен­циальным уравнениям и требует большого объема тригонометри­ческих преобразований. Символический методпозволяет тригоно­метрические операции над гармоническими колебаниями и геомет­рические операции над векторами свести к алгебраическим опера­циям над комплексными числами, что существенно упрощает рас­чет. При этом могут быть использованы все методы преобразова­ний и анализа, изложенные в гл. 1, 2. Допустимость использования символического метода объясняется тем, что в линейных цепях в режиме гармонических воздействий в цепи устанавливаются гармо­нические колебания тон же частоты. Таким образом, неизвестными параметрами токов и напряжений будут лишь амплитуды и фазы, определяемые однозначно их комплексными амплитудами. Запишем основные законы электрических цепей в символической форме.

Для резистивного элемента R связь между комплексными ам­плитудами тока I_т и напряжения U_т можно определить согласно закону Ома (1.6) путем замены мгновенных значений токов iи на­пряжений и их комплексными амплитудами:

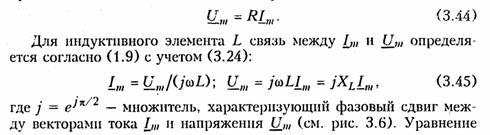
(3.45) отражает закон Ома для индуктивных элементов. Сравнение (3.45) с (1.9) показывает, что операция дифференцирования d/dt соответствует в комплексной форме умножению на jω.

Для емкостного элемента С на основании (1.12) можно записать:

т. е. операция интегрирования соответствует в комплексной форме делению на/со. Полученные уравнения (3.44) —(3.46) справедливы и для комплексных действующих значений токов и напряжений:

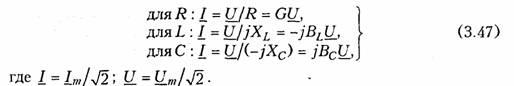
Аналогично можно получить уравнения законов Кирхгофа в комплексной форме. Так, для ЗТК (1.16) заменив мгновенные зна­чения токов i_k их комплексными амплитудами I_mk, получим

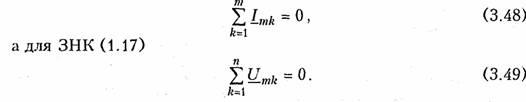
Полученные уравнения законов Ома и Кирхгофа в комплексной форме лежат в основе символического метода расчета линейных цепей при гармонических воздействиях. Причем, как показывает анализ уравнений (3.24), (3.26). (3.45) и (3.46), при переходе к комплексной записи операции дифференцирования заменяются ум­ножением на jω, операции интегрирования — делением на jω. В результате вместо системы интегрально-дифференциальных урав­нений получаем систему алгебраических уравнений, решение кото­рой определяет амплитуды и начальные фазы искомых токов и напряжений.

Применим символический метод к анализу гармонических ко­лебаний в цепи при последовательном (см. § 3.4) и параллельном (см. § 3.5) соединениях элементов R, L, С. Для последовательного

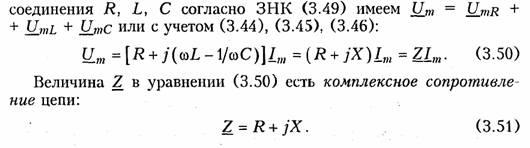
Комплексное сопротивление Z можно выразить в показательной или тригонометрической форме:

Таким образом, рассмотренное ранее полное сопротивление цепи (3.33) представляет собой модуль комплексного сопротивления:

а фазовый сдвиг φ — аргумент (arg) комплексного сопротивления:

Аналогичным образом можно получить уравнения токов и на­пряжений в комплексной форме для параллельного соединения элементов R, L, С (см. § 3.5). Так уравнение (3.39) в комплексной форме примет вид

Следовательно, полная проводимость цепи Y равна модулю комплексной проводимости Y = | Y‌‌‌‌‌‌‌|, а фазовый сдвиг φ — аргумен­ту комплексной проводимости φ = arg Y = arctg(B/G).

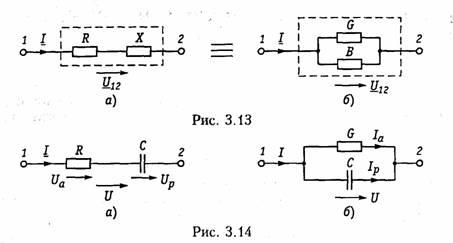
При анализе различных электрических цепей часто возникает необходимость преобразования схемы последовательно соединен­ных элементов в эквивалентное параллельное соединение и нао­борот (рис. 3.13). В основе подобных преобразований лежит прин­цип эквивалентности (см. § 1.5). Согласно этому принципу ток I и напряжение U₁₂ в исходной (рис. 3.13, а) и преобразованной (рис. 3.13, б) схемах должны остаться неизменными. Для первой

Преобразование (3.56) и (3.57) можно положить в основу раз­ложения тока в последовательном участке и напряжения в па­раллельном на активную и реактивную составляющие.

Пример. Преобразовать последовательный RC-участок (рис 3.14, я) в эк­вивалентный параллельный (рис. 3.14, б). Определить активные и реактивные составляющие токов и напряжений на обоих участках.

В соответствии с уравнением (3.57) получаем

Символический метод особенно эффективен при анализе слож­ных разветвленных цепей. Причем поскольку все методы расчета подобных цепей (метод контурных токов, узловых потенциалов, наложения и др.) базируются на законах Ома и Кирхгофа, то эти методы могут использоваться и при комплексной форме с заменой соответствующих величин (токов, напряжений, сопротивлений, проводимостей) их комплексными значениями.

Пример. Проиллюстрируем это на примере расчета цепи, изображенной на рис. 3.15 различными методами в комплексной форме. Заменим элементы вет­вей в исходной схеме их комплексными сопротивлениями, а источники на­пряжения и токи их комплексными значениями (рис. 3.16):

Рассчитаем теперь эту цепь различными методами в символической форме, используя комплексы действующих значений токов и напряжений.

1.   Метод наложения.   Сравнение схем,   изображенных  на рис.   3.16  и рис. 2.5. а показывает их одинаковую топологию. Таким образом, путем пере­хода от R к Z, от U_r к U_r и от I к Iможно сразу получить соответствующие уравнения для токов I _1, I _2, I ₃(см. § 2.3).

2.  Метод контурных токов. В соответствии с § 2.4 составляем систему из двух уравнений для контуров I и II:

 

писать уравнения для мгновенных значений i и и. Так, если угловая частота задающих источников синусоидальных колебаний u_r1 и u_r2 равна ω, то мгно­венное   значение   тока   

 

Аналогичным образом осуществляется преобразование элект­рических цепей, содержащих комплексные сопротивления. Комплексные сопротивления, соединенные звездой преобразу­ются в треугольник путем замены в формулах (2.6)—(2.9) па­раметров R и G на соответствующие комплексы Z и Y. Точно также осуществляется обратное преобразование треугольник-звезда.

Например, с учетом уравнений (1.9) и (1.12) можно получить формулы преобразования «звезда—треугольник» индуктивных и емкостных элементов. Так, для емкостных элементов при преоб­разовании «треугольник—звезда» имеем:

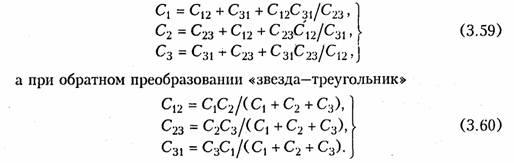
Преобразование «треугольник—звезда» и обратно для индук­тивных элементов осуществляется по формулам, аналогичным (2.6)-(2.8).

Подобным же образом преобразуются матрично-топологические уравнения цепей в комплексную форму. Например, матричные уравнения (1.18), (1.20), (2.17) в комплексной форме принимают следующий вид:

где Y_B, Y_y — матрицы комплексной проводимости ветвей и комп­лексной узловой проводимости.

Z_B, Z_K — матрица комплексного сопротивления ветви и матрица комплексного контурного сопротивления.

Uгв, JГB, Uв — матрицы-столбцы комплексных задающих напря­жений и токов ветви и напряжений ветвей.