1.2. Электрическая цепь, ее элементы и модели

 

Электрической цепью называют совокупность устройств, пред­назначенных для прохождения тока п описываемых с помощью понятий тока п напряжения. Электрическая пень состоит из ис­точников (генераторов) и приемников электрической энергии.

Источником называют устройство, создающее (генерирующее) токи п напряжения. В качестве источников могут выступать как первичные устройства, преобразующие различные виды энергии в электрическую (аккумуляторы, электромашинные генераторы, тер­моэлементы, пьезодатчики п т. д.), так и устройства, преобразую­щие электрическую энергию первичных источников в энергию электрических колебаний требуемой формы.

Приемником называют устройство, потребляющее (запасающее) пли преобразующее электрическую энергию в другие виды энергии (тепловую, механическую, световую и т. д.). Физическими элемен­тами реальной электрической цепи являются резисторы, катушки индуктивности, конденсаторы, трансформаторы, транзисторы, электронные лампы и другие компоненты электроники. При этом электрическая цепь может конструктивно выполняться либо из указанных выше дискретных компонентов, либо изготовляться в едином технологическом цикле (интегральные схемы). Электри­ческие цени, содержащие как интегральные, так и дискретные компоненты, получили наименование гибридных.

В основе теории электрических цепей лежит принцип модели­рования. При этом реальные электрические цепи заменяются не­которой идеализированной моделью, состоящей из взаимосвязан­ных идеализированных элементов. Последние представляют собой простые модели, используемые для аппроксимации (приближения) свойств простых физических элементов или физических явлений. В зависимости от точности приближения одна и та же физическая электрическая цепь может быть представлена различными моде­лями, причем, чем точнее модель, тем она сложнее. На практике обычно ограничиваются  наиболее простыми  моделями,  обеспечивающими решение задач

анализа и синтеза реальной цепи с за­данной точностью. Важно иметь в виду, что если физические эле­менты и явления могут быть описаны лишь приближенно, то идеа­лизированные элементы определяются точно. К простейшим идеа­лизированным элементам модели электрической цепи относятся не­зависимые и зависимые источники (активные элементы) и эле­менты резистивного сопротивления, индуктивности и емкости (пас­сивные элементы).

Систему уравнений, описывающую модель электрической цепи, называют математической моделью цепи. В теории электриче­ских цепей изучаются общие свойства моделей цепей, поэтому в дальнейшем под электрической цепью будем понимать ее модель, свойства которой близки к свойствам реальной физической цепи.

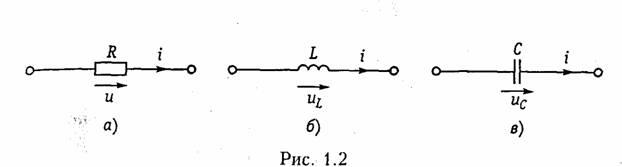
Пассивные элементы. Резистивным сопротивлением называют идеализированный элемент, обладающий только свойством необра­тимого рассеивания энергии. Условное обозначение резистивного сопротивления показано на рис. 1.2, а. Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома:

Коэффициенты пропорциональности R и G в формулах (1.6) на­зываются соответственно сопротивлением и проводимостью эле­мента и являются его количественной характеристикой, причем при согласованных направлениях тока и напряжения R и G по­ложительны и связаны обратной зависимостью R = 1/G. Измеряют в системе СИ сопротивление R в омах (Ом), а проводимость G— в сименсах (См).

Уравнение (1.6) определяет зависимость напряжения от тока и носит название вольт-амперной характеристики (ВАХ) резис­тивного сопротивления. Если R постоянно, то ВАХ линейна (рис. 1.3, а) и соответствует линейному резистивному элементу. Если же R зависит от протекающего через него тока или прило­женного к нему напряжения, то ВАХ становится нелинейной (рис. 1.3, б) и соответствует нелинейному резистивному сопротив­лению.

Мощность в резистивном сопротивлении можно определить со­гласно уравнению (1.5):

 

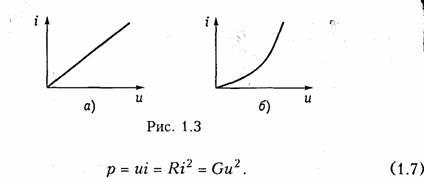
Мощность в резистивном сопротивлении всегда больше нуля, так как оно только потребляет энергию, преобразуя ее в тепло или другие виды энергии.

Индуктивным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накопления им энергии магнитного поля. Условное обозначение индуктивного элемента изображено на рис. 1.2, б.

Математическая модель, описывающая свойства индуктивного элемента определяется соотношением

где ψ — потокосцепление, характеризующее суммарный магнитный поток, пронизывающий катушку:

Коэффициент пропорциональности L в формуле (1.8) называ­ется индуктивностью. Он имеет положительное значение и является количественной характеристикой индуктивного элемента. Из­меряется индуктивность L в генри (Гн), а магнитный поток Ф — в веберах (Вб). Если величина L постоянна, то зависимость (1.8); {вебер-амперная характеристика} линейна и соответствует линейному индуктивному элементу. Если же L зависит от электричес­кого режима (тока или напряжения), то зависимость (1.8) нелинейна и соответствует нелинейному элементу индуктивности.           

Связь между током и напряжением на индуктивном элементе определяется согласно закону электромагнитной индукции выражением      

т. е. напряжение на индуктивном элементе пропорционально ско­рости  изменения протекающего через  него тока.   Следовательно, при протекании через L постоянного тока u = 0 и свойства индук­тивного элемента эквивалентны коротко замкнутому (КЗ) участку (_См. рис. 1.1, а).

Мгновенная мощность электрических колебаний в индуктивном элементе

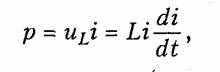
т.е. может быть как положительной (при совпадении направлений и и i), так и отрицательной (при несовпадении направлений и и i). Причем в первом случае (р>0) магнитная энергия запасается ин­дуктивным элементом, а во втором (р<0) — отдается во внешнюю цепь.

Энергия, запасенная в индуктивном элементе к моменту t, оп­ределится согласно (1.4)

т. е. всегда полoжительна.

Емкостным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накапливать энергию электрического поля. Условное обозначение емкостного элемента показано на рис. 1.2, в.

Математическая модель, описывающая свойства емкостного элемента, определяется вольт-кулонной характеристикой

q = Cu_c.                                     (1.11)

Коэффициент пропорциональности С в формуле (1.11) назы­вается емкостью и является количественной характеристикой ем­костного элемента. При согласованных направлениях тока и на­пряжения величина С всегда положительна. Измеряется С в фара­дах (Ф).

Если величина С постоянная, то вольт-кулонная характеристика (1.11) линейна и соответствует линейному емкостному элементу. Если же параметр С зависит от электрического режима, то харак­теристика (1.11) нелинейна и соответствует нелинейному элементу.

Между током и напряжением на емкостном элементе существует связь, определяемая согласно (1.1) и (1.11) равенством

т. е. ток в емкостном элементе пропорционален скорости изменения приложенного к нему напряжения. При постоянном напряжении и=const, i = 0 и емкостной элемент по своим свойствам эк­вивалентен разрыву цепи.

Мощность электрических колебаний в емкостном элементе

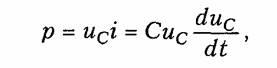
т. е. может быть как положительной, так и отрицательной в зави­симости от направлений тока и напряжения. При р>0 энергия электрического поля запасается емкостным элементом, а при р<0 — отдается во внешнюю цепь.

Энергия, запасенная в емкостном элементе к моменту t,

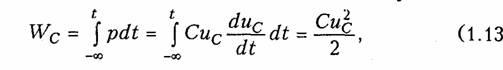
т. е. всегда положительна.

В инженерной практике резистивное сопротивление, индуктив­ный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя, по существу, элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумениям, также будем пользоваться этой терминологией.   

Рассмотренные идеализированные резистивный, индуктивный и емкостной элементы могут служить простейшими моделями резис­торов, высококачественных' катушек индуктивностей с малыми потерями и электрических конденсаторов с высокими диэлектричес­кими свойствами в области низких и средних частот. В области высоких, а особенно сверхвысоких частот модели резисторов, катушек индуктивности и конденсаторов становятся более сложными.Так, на высоких частотах резисторы уже нельзя с достаточной точностью описать идеальным резистивным элементом (1.6) из-за влияния различных «паразитных» емкостей.  Более точной здесь будет модель

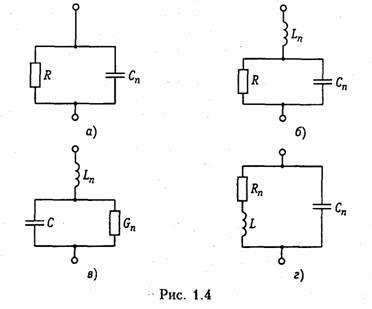
параллельного соединения R и С_П, изображенная на рис. 1.4, а. В некоторых случаях возникает необходимость учета, «паразитной» индуктивности L_П, учитывающей эффект накопления энергии магнитного поля в элементах резистора (рис. 1.4, б).

На высоких и сверхвысоких частотах также начинает прояв­ляться поверхностный эффект, выражающийся в неравномерном распределении тока по сечению проводника {скип-эффект). В ре­зультате этого сопротивление R проводника начинает расти с уве­личением частоты. Причем, чем толще проводник, тем при мень­ших частотах начинает проявляться скип-эффект. На сверхвысо­ких частотах зависимость сопротивления круглого медного про­водника от частоты f можно выразить эмпирической формулой

где Ro — сопротивление проводника постоянному току, Ом; d — диаметр сечения проводника, мм; f — частота, МГц.

Модель конденсатора, кроме емкостного элемента С, может со­держать параллельную проводимость G_П, учитывающую потерн , энергии в диэлектрике, и последовательную индуктивность L_П, учитывающую эффект запасения энергии магнитного поля в кон­структивных элементах конденсатора (рис. 1.4, в).

Модель катушки индуктивности может учитывать потери энер­гии в проводе и энергию электрического поля, запасаемую между витками катушки путем дополнительного включения сопротивления потерн R_П и «паразитной» емкости С_П (рис. 1.4, г).

В зависимости от условий применения и конструктивных осо­бенностей, требований к точности анализа могут использоваться и более сложные модели резисторов, катушек индуктивностей и кон­денсаторов.

В зависимости от соотношения между длинами цепи l и волны тока п напряжения λ различают цепи с сосредоточенными и рас­пределенными параметрами. При l<λ можно считать, что пара­метры R, L, С сосредоточены в резисторах, катушках индуктив­ности и конденсаторах; при l>> λ необходимо пользоваться моде­лью цепи с распределенными параметрами (см. гл. 13).

Рассмотренные выше резистивные индуктивные и емкостные элементы относятся к двухполюсным, так как содержат только два зажима (полюса, вывода). Однако кроме двухполюсных элементов в теории цепей и электронике широко используются трехполюсные, четырехполюсные и многополюсные элементы. Напри­мер, свойства трансформатора как физического устройства, содер­жащего две индуктивно связанные катушки, не могут быть описа­ны моделью только двухполюсных элементов с индуктивностями L₁ и L₂. Для его моделирования необходимо введение еще одного параметра  —  взаимной   индуктивности  М;   при  этом  моделью

трансформатора  будет  являться  четырехполюсный  элемент  (см. гл. 3).

Активные элементы. Активными элементами электрической це­пи являются зависимые и независимые источники электрической энергии. К зависимым источникам относятся электронные лампы, транзисторы, операционные усилители и другие, к независимым источникам — аккумуляторы, электрогенераторы, термоэлементы, пьезодатчики и другие преобразователи. Независимые источники можно представить в виде двух моделей: источника напряжения и источника тока.

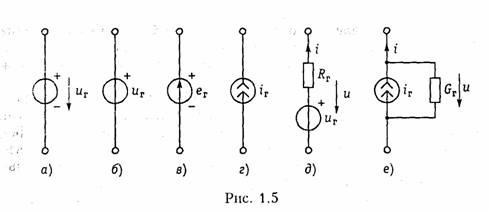
Независимым источником напряжения называют идеализиро­ванный двухполюсный элемент, напряжение на зажимах которого не зависит от протекающего через него тока. Условное обозначение источника напряжения показано на рис. 1.5, а.

Источник напряжения полностью характеризуется своим задаю­щим напряжением щ, или электродвижущей силой (ЭДС) е_Г(рис. 1.5, в). Внутреннее сопротивление источника напряжения равно нулю н иногда при изображении источника напряжения обо­значают знаком «+>> только один из зажимов и не показывают стрелкой положительное направление е_Г имея в виду, что оно дей­ствует от «+» к «—» (рис. 1.5, б). Часто при анализе цепей ограни­чиваются изображением только зажимов источника напряжения, как показано на рис. 1.1, б.

Вольт-амперная характеристика идеального источника напря­жения представляет собой прямую, параллельную оси токов (рис. 1.6. а). Такой идеализированный источник способен отдавать во внешнюю цепь бесконечно большую мощность. Ясно, что физически такой источник реализовать нельзя. Однако в определенных пределах изменения тока он достаточно близко отражает ре­альные свойства независимых источников.

Независимым источником тока называют идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах.  Условное обозначение источника тока показано на рис.  1.5,  г.  Источник тока полностью характеризуется своим задающим током i_Г. Внутренняя проводимость источника тока равна нулю (внутреннее со­противление бесконечно вели­ко) и ВАХ представляет собой прямую, параллельную осп на­пряжений (рис. 1.6, б). Такой источник также способен отда­вать во внешнюю цепь бесконечно большую мощность и является идеализацией реальных неза­висимых источников.

Свойства реальных источников с конечным внутренним сопро­тивлением R_T можно моделировать с помощью независимых ис­точников напряжения и тока с дополнительно включенными резистивными сопротивлениями R_Г или проводимостью G_Г (см. рис. 1.5, д, е). Напряжение и и отдаваемый ток i этих источников зависят от параметров подключаемой к ним цепи, а их В АХ имеет тангенс угла наклона α, пропорциональный R_Г и G_Г соответственно (штриховые линии па рис. 1.6).

Однако свойства целого ряда электронных устройств нельзя описать моделью соединенных между собой указанных выше не­зависимых источников и пассивных двухполюсных элементов. К числу таких устройств относятся электронные лампы, транзисторы, операционные усилители и другие электронные приборы. Это так называемые зависимые пли управляемые источники.

Зависимый источник представляет собой четырехполюспый элемент (рис. 1.7) с двумя парами зажимов — входных (/, /') н выходных (2, 2'). Входные ток i₁ и напряжение и₁ являются уп­равляющими. Различают следующие разновидности зависимых источников:     источник  напряжения,   управляемый  напряжением

 

 

(ИНУН); источник тока, управляемый напряжением (ИТУН); ис­точник напряжения, управляемый током (ИНУТ); источник тока управляемый током (ИТУТ). На рис. 1.7 показаны условные обо­значения зависимых источников различного типа.

В ИНУН (рис. 1.7, а) входное сопротивление бесконечно ве­лико, входной ток i₁= 0, а выходное напряжение и₂ связано со входным и₁ равенством и₂ — H_uu₁, где Н и — коэффициент, харак­теризующий усиление по напряжению зависимого источника. Ис­точник типа ИНУН является идеальным усилителем напряжения.

 ИТУН (см. рис. 1.7, б) выходной ток i₂ управляется вход­ным напряжением u₁ причем i₁= 0 и ток i₂ связан с и₁ равенством  где Н_G — коэффициент, имеющий размерность прово­димости.

В ИНУТ (рис. 1.7, е) входным током i₁ управляется выходное напряжение i₂, входная проводимость бесконечно велика: u₁=0, i₂ =H_I i_2 1, где Hi— коэффициент, имеющий размерность сопротив­ления.

В ИТУТ (рис. 1.7, г) управляющим током является i₁, а уп­равляемым i₂. Входная проводимость ИТУТ, как и ИНУТ, беско­нечно велика,  где Hi —коэффициент, характери­зующий усиление по току. Источник типа ИТУТ является идеаль­ным усилителем тока. Коэффициенты Н_u Н_G, HR, Hi, представ­ляют собой вещественные положительные или отрицательные числа и полностью характеризуют соответствующий источник.

Примером зависимого источника является операционный уси­литель (ОУ). Выпускаемые в виде отдельной микросхемы (рис. 1.8, а) ОУ широко применяются в качестве активных эле­ментов электрической цепи.

Операционный усилитель имеет два входа: 1 — неинвертирующий и 2 — инвертирующий. При подаче напряжения и₁ на вход 1 — выходное напряжение u₂ имеет ту же полярность, что и u₂ а

 

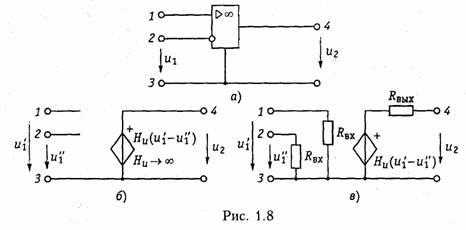
при подаче u₂на вход 2 напряжение u₂ меняет свою полярность па противоположную.

Идеальный ОУ (рис. 1.8, б) представляет собой ИНУН с бес­конечно большим коэффициентом усиления (Ни→∞), бесконечно большими входным сопротивлением и выходной проводимостью (выходное сопротивление равно нулю).

Реальный ОУ можно представить в виде ИНУНа с конечными входным R_BX и выходным R_вых сопротивлениями (рис. 1.8, в).

Кроме ОУ в качестве активных элементов электрических цепей широко используются различные электронные и полупроводнико­вые приборы: электронные лампы, биполярные и полевые транзис­торы и др.

На рис. 1.9, а приведена электронная лампа (триод) и ее модели (эквивалентные схемы замещения) в форме ИТУН (рис. 1.9, б) и ИНУН (рис. 1.9, в), где обозначены Gi = 1/Ri, — внутренняя про­водимость лампы, S = di₂/du — крутизна; μ = SRi, — коэффициент усиления лампы. Параметры G i, S, μ обычно приводятся в спра­вочниках. Эти эквивалентные схемы являются линейными и могут использоваться в области низких частот. В нелинейном режиме ра­боты активного элемента используются более сложные модели (см. гл. 10, 11). В области высоких частот в моделях активных элемен­тов появляются кроме резисторов, реактивные элементы — обычно емкость (см. табл. 1.1).

 

 

 

 

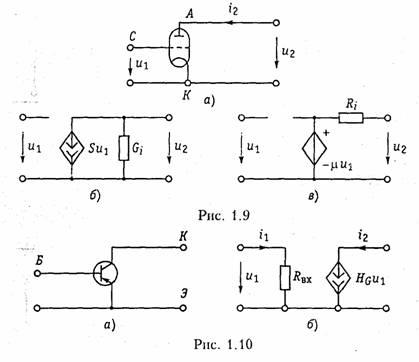
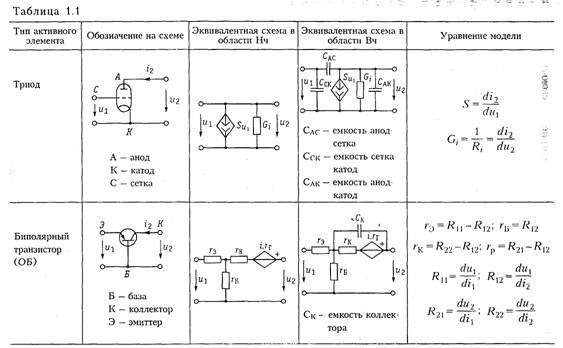
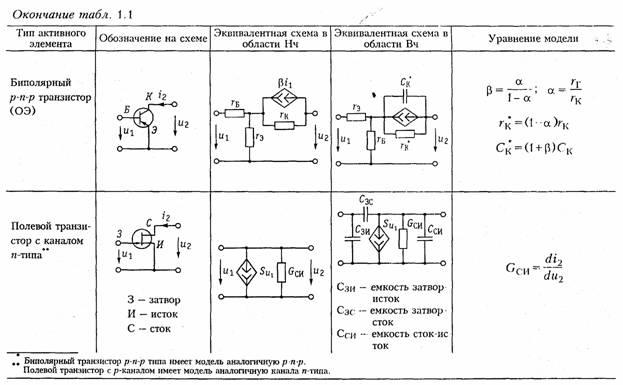
Транзисторы, как правило, имеют более сложную структуру, чем лампы и описываются в зависимости от решаемых задач более сложными моделями [2]. Наиболее распространенными для бипо­лярных транзисторов являются образные и /7-образные эк­вивалентные схемы замещения, причем, последние можно получить из первых методами преобразования «звезда — треугольник» (см. § 1.5). В табл. 1.1 приведены образные схемы замещения бипо­лярных транзисторов, включенных по схеме с общей базой (ОБ) и общим эмиттером (ОЭ) в области низких и высоких частот и ос­новные соотношения, описывающие их модели.

Иногда для анализа цепей с биполярными транзисторами ис­пользуются модель ИТУН с конечным входным сопротивлением (рис. 1.10). Для полевых транзисторов обычно используется мо­дель в форме ИТУН (табл. 1.1).

Кроме рассмотренных эквивалентных схем нередко (особенно в справочной литературе) электронные лампы и транзисторы рас­сматриваются как бесструктурные четырехполюсники с той или иной системой параметров (см. гл. 12).

Отличительной особенностью зависимых источников является их необратимость, т. е. цепи с этими источниками имеют четко выраженный вход и выход. Таким образом, для цепей с зависи­мыми источниками различают путь прямого прохождения сигнала (от входа к выходу) и обратного прохождения (с выхода на вход), реализуемого с помощью специальных цепей обратной свя­зи (ОС) (гл. 14). Необходимость введения в активные цепи ОС объясняется рядом важных качеств, которыми эти цепи обладают: возможностью моделирования различных функций (см. § 2.7) (суммирование, интегрирование, дифференцирование и др.), ге­нерированием и усилением колебаний, моделированием пассивных элементов типа R, L, С и их преобразованием (например, С и L), перемещение нулей и полюсов функции цепи (см. гл. 14, 15) и др.