
- •Математическая статистика в примерах и задачах
- •Рецензент
- •Оглавление
- •Предисловие
- •Модуль 1. Анализ вариационных рядов
- •1.1. Генеральная совокупность. Выборочный метод. Графическое и табличное представление данных Опорный конспект
- •Вопросы для самоконтроля
- •Образцы решения типовых задач
- •Задачи для самостоятельного решения
- •1.2. Выборочные числовые характеристики Опорный конспект
- •Вопросы для самоконтроля
- •Образцы решения типовых задач
- •Задачи для самостоятельного решения
- •1.3. Точечные оценки. Методы нахождения точечных оценок Опорный конспект
- •Вопросы для самоконтроля
- •Образцы решения типовых задач
- •Задачи для самостоятельного решения
- •1.4. Доверительные интервалы Опорный конспект
- •Вопросы для самоконтроля
- •Образцы решения типовых задач
- •Задачи для самостоятельного решения
- •1.5 Проверка статистических гипотез Опорный конспект
- •Вопросы для самоконтроля
- •Образцы решения типовых задач
- •Задачи для самостоятельного решения
- •Модуль 2. Линейная регрессия. Элементы корреляционного анализа
- •Вопросы для самоконтроля
- •Образцы решения типовых задач
- •Задачи для самостоятельного решения
- •Индивидуальные домашние задания.
- •Приложение
- •Литература
Вопросы для самоконтроля
1. Как ставится задача об оценке неизвестных параметров, входящих в закон распределения случайной величины?
2. Что называется точечной оценкой неизвестного параметра распределения?
3. Какая точечная оценка называется несмещенной?
4. Какая точечная оценка называется состоятельной?
5. Какая точечная оценка называется эффективной?
6. Будет ли выборочное среднее несмещенной и состоя-тельной оценкой для математического ожидания генеральной совокупности?
7. Выяснить, смещенная или несмещенная выборочная дисперсия.
8.
Исправленная выборочная дисперсия
![]() является
несме-щенной
и состоятельной
оценкой для дисперсии
генеральной
совокупности?
является
несме-щенной
и состоятельной
оценкой для дисперсии
генеральной
совокупности?
9. Какое предположение о распределении наблюдаемой случайной величины делается при применении методов моментов и метода максимального правдоподобия.
10. Опишите получение точечных оценок параметров распределения методом моментов.
11. Опишите получение точечных оценок параметров распределения методом максимального правдоподобия.
12. Объясните, чем вызван переход от функции правдоподобия к ее логарифму.
13. Опишите получение точечных оценок параметров распределения методом наименьших квадратов.
Образцы решения типовых задач
Пример 1. Известно, что число независимых опытов до первого появления события имеет геометрический закон распределения:
|
|
1 |
2 |
3 |
… |
k |
… |
|
|
р |
qp |
q2p |
… |
qk-1p |
… |
где
p
– неизвестный параметр, который равен
вероятности появления события в одном
опыте, q
= 1 – p.
Проделано 5 серий опытов до первого
появления события. Они дали следующие
результаты: ![]() ,
,
![]() ,
x3 = 2,
x4 = 11,
x5 = 3.
Найти оценку наибольшего правдоподобия
для р.
Оценить р
по методу моментов.
,
x3 = 2,
x4 = 11,
x5 = 3.
Найти оценку наибольшего правдоподобия
для р.
Оценить р
по методу моментов.
Решение. Найдем функцию правдоподобия в общем случае

Тогда



В
нашем случае  .
Значит
.
Значит

Используя
метод моментов получаем такую же оценку,
так как  А оценкой
А оценкой ![]() является
является
![]() .
.
Пример
2. Случайная
величина Х
(отклонение контролируемого размера
изделия от номинала) подчинена нормальному
закону распределения с неизвестными
параметрами а
и ![]() .
Ниже приведена таблица наблюдаемых
отклонений от номинала, подвepгнyтыx
группировке, для n
= 200 изделий
(в первой строке указаны середины
интервалов отклонений
.
Ниже приведена таблица наблюдаемых
отклонений от номинала, подвepгнyтыx
группировке, для n
= 200 изделий
(в первой строке указаны середины
интервалов отклонений
![]() (мм); во второй
строке приведена частота mi
– число
наблюдений, попадающих в данный интервал):
(мм); во второй
строке приведена частота mi
– число
наблюдений, попадающих в данный интервал):
|
|
0,3 |
0,5 |
0,7 |
0,9 |
1,1 |
1,3 |
1,5 |
1,7 |
1,9 |
2,2 |
2,3 |
|
mi |
6 |
9 |
26 |
25 |
30 |
26 |
21 |
24 |
20 |
8 |
5 |
Найти
методом моментов точечные оценки
неизвестных параметров a
и
![]() нормального распределения.
нормального распределения.
Решение. Для нахождения двух неизвестных параметров необходимо два уравнения. Первое получаем, приравнивая начальный теоретический момент первого порядка к начальному эмпирическому моменту первого порядка, а второе – приравнивая центральный теоретический момент второго порядка к центральному эмпирическому моменту второго порядка:
![]() ,
,
![]()
Находим
величины
![]() и
и
![]() по данным
выборки:
по данным
выборки:

![]()
Для
нахождения выборочной дисперсии перейдем
к условным вариантам
![]() :
:
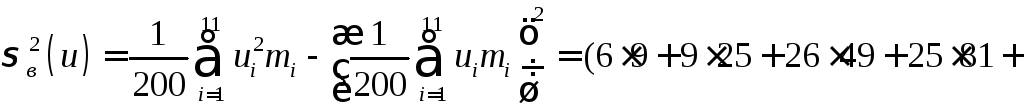
![]()
![]()
![]()

(при больших n исправленная и неисправленная выборочные дисперсии мало различаются); s = 0,498.
Пример
3. Предполагается,
что выполнение некоторой работы занимает
случайное время с распределением
Симпсона на отрезке ![]() .
Хронометраж 20 испытаний дал среднее
время работы 30 мин. и исправленную
выборочную дисперсию 24 мин2.
Оценить параметры а
и b
методом моментов. Оценить, за какое
время работа будет выполняться с
вероятностью 98 %.
.
Хронометраж 20 испытаний дал среднее
время работы 30 мин. и исправленную
выборочную дисперсию 24 мин2.
Оценить параметры а
и b
методом моментов. Оценить, за какое
время работа будет выполняться с
вероятностью 98 %.
Решение.
Для
распределения Симпсона (плотность
которого имеет вид равнобедренного
треугольника с основанием на заданном
отрезке) имеем:
 ,
, .
.
Параметры распределения можно выразить через среднее и дисперсию:
![]() ,
,
![]()
Подставляя
вместо теоретических моментов выборочные,
получаем оценки
![]() ,
,![]() ,
откуда
,
откуда![]() (мин.),
(мин.),![]() = 42 (мин.).
= 42 (мин.).
Функция распределения Симпсона имеет вид:
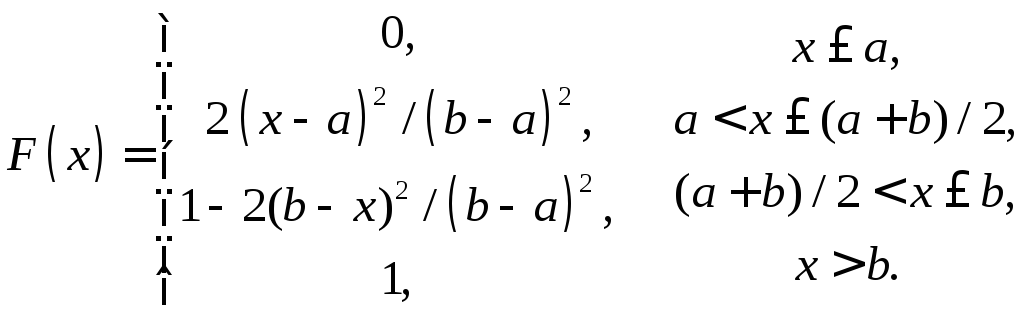
Решая
уравнение ![]() ,
находим искомое время:
,
находим искомое время:
![]() .
Подставляя полученные оценки в формулу
вместо теоретических параметров,
получаем:
.
Подставляя полученные оценки в формулу
вместо теоретических параметров,
получаем:![]() =
42 – 0,1
=
42 – 0,1![]() (42 – –18) = 39,6(мин.).
(42 – –18) = 39,6(мин.).
Пример 4. Найти методом максимального правдоподобия оценку вероятности «успеха» в схеме испытаний Бернулли.
Решение. Рассмотрим случайную величину Х: Х = 1 если имеет место «успех»; Х = 0 если имеет место «неудача». Тогда функция вероятностей случайной величины Х запишется в виде:

Логарифмическая функция правдоподобия для одного испытания будет иметь вид

Для
n
испытаний и m
«успехов» в n
испытаниях
![]() .
.
Отсюда
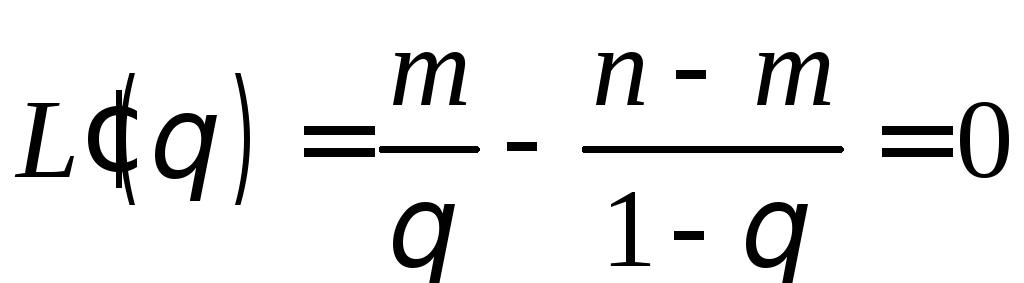 и
и .
Проверим знак второй производной:
.
Проверим знак второй производной: .
Таким образом, относительная частота
события и является оценкой вероятности
«успеха» в одном испытании Бернулли,
найденной методом максимального
правдоподобия. Поскольку
.
Таким образом, относительная частота
события и является оценкой вероятности
«успеха» в одном испытании Бернулли,
найденной методом максимального
правдоподобия. Поскольку![]() ,
то
,
то![]() является несмещенной оценкой вероятности.
является несмещенной оценкой вероятности.
Пример
5. Случайная
величина Х
(число поврежденных стеклянных
изделий в одном контейнере) распределена
по закону Пуассона с неизвестным
параметром
![]() .
Ниже приведено эмпирическое распределение
числа поврежденных изделий в 500 контейнерах
(в первой строке указано количествоxi
поврежденных изделий в одном
контейнере, во второй строке приведена
частота
.
Ниже приведено эмпирическое распределение
числа поврежденных изделий в 500 контейнерах
(в первой строке указано количествоxi
поврежденных изделий в одном
контейнере, во второй строке приведена
частота ![]() – число
контейнеров, содержащих xi
поврежденных изделий):
– число
контейнеров, содержащих xi
поврежденных изделий):
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
199 |
169 |
87 |
31 |
9 |
3 |
1 |
1 |
Найти
методом максимального правдоподобия
точечную оценку неизвестного параметра
![]() распределения Пуассона.
распределения Пуассона.
Решение. Выпишем функцию правдоподобия в виде:

Найдем
точку максимума логарифмической функции
правдоподобия, для чего приравняем
к нулю ее первую производную по
![]() :
:
 ,
,
 .
.
Получаем
![]() .
Убедимся, что полученное
.
Убедимся, что полученное![]() является точкой максимума, для чего
найдем вторую производную и проверим
ее знак в точке
является точкой максимума, для чего
найдем вторую производную и проверим
ее знак в точке
![]() :
:
 .
.
Если
в последнее уравнение подставить
![]() ,
то вторая производная будет
отрицательной, а значит,
,
то вторая производная будет
отрицательной, а значит,
![]() является
точкой максимума. Найдем значение
является
точкой максимума. Найдем значение
![]() для рассматриваемого примера:
для рассматриваемого примера:
![]()
 .
.
Пример
7. Найти
методом максимального правдоподобия
по выборке ![]() точечные оценки параметров а
и
точечные оценки параметров а
и ![]() нормального
распределения, плотность которого
нормального
распределения, плотность которого
 .
.
Решение. Выпишем функцию правдоподобия в виде:
 .
.
Логарифмическая функция правдоподобия имеет вид

Найдем точку максимума, решив систему из двух уравнений, получающихся путем приравнивания к нулю первых двух частных производных по неизвестным параметрам:


 .
.
Проверим,
является ли точка ![]() точкой максимума функции правдоподобия:
точкой максимума функции правдоподобия:

Как
известно из математического анализа,
чтобы функция ![]() достигала максимума
в некоторой точке, достаточно, чтобы
матрица второго дифференциала функции
достигала максимума
в некоторой точке, достаточно, чтобы
матрица второго дифференциала функции
![]() в этой точке
была определена отрицательно. По критерию
Сильвестра для этого необходимо и
достаточно, чтобы ее главные миноры
чередовались по знаку, а именно
в этой точке
была определена отрицательно. По критерию
Сильвестра для этого необходимо и
достаточно, чтобы ее главные миноры
чередовались по знаку, а именно ![]() .
Рассмотрим матрицу производных:
.
Рассмотрим матрицу производных:

Отсюда
 ;
;
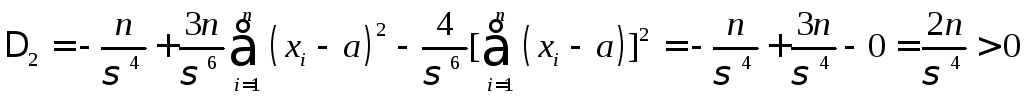 .
.
Следовательно,
точка
![]() – действительно точка максимума, и
полученные оценки являются оценками
максимального правдоподобия.
– действительно точка максимума, и
полученные оценки являются оценками
максимального правдоподобия.
Пример
8. Найти
оценку максимального правдоподобия
для параметра сдвига
![]() распределения Коши, заданного плотностью
распределения Коши, заданного плотностью по выборке из двух наблюдений, если:
по выборке из двух наблюдений, если:
а)
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() .
.
Решение. Функция правдоподобия для двух наблюдений имеет вид
 .
.
Введем
функцию
 ,
тогда задача максимизации функции
правдоподобия эквивалентна задаче
минимизации
,
тогда задача максимизации функции
правдоподобия эквивалентна задаче
минимизации![]() .
.
а)
если
![]() ,
,
![]() ,
то
,
то
![]()
![]() Функция R
достигает минимума в точке
Функция R
достигает минимума в точке
![]() ,
так что это и есть оценка максимального
правдоподобия;
,
так что это и есть оценка максимального
правдоподобия;
б)
если
![]() ,
,
![]() то
то
![]()
![]() ,
и производная
,
и производная ![]() будет иметь три нулевых значения: в
точках
будет иметь три нулевых значения: в
точках
![]() и
и![]() .
При этом точка
.
При этом точка![]() оказывается точкой максимума. Точкам
оказывается точкой максимума. Точкам![]() соответствует
минимум
R, причем в
обеих этих точках величина R
одинакова. Таким образом, оба значения
соответствует
минимум
R, причем в
обеих этих точках величина R
одинакова. Таким образом, оба значения
![]() являются
в данном случае оценками максимального
правдоподобия.
являются
в данном случае оценками максимального
правдоподобия.
Замечание.
Ни метод моментов, ни метод максимального
правдоподобия не могут дать хороших
оценок для параметра сдвига
распределения Коши. Тем не менее
существует простая оценка для него –
выборочная медиана: ![]() поскольку
поскольку
 .
.
Пример 9. Найти методом максимального правдоподобия оценки параметров а и b равномерного закона распределения:

Решение.
Для равномерного
закона не выполняется одно из условий
регулярности, так как область возможных
значений исследуемой случайной величины,
в которой
![]() ,
зависит в данном случае от
,
зависит в данном случае от![]() ,
где
,
где![]() – оцениваемый параметр или вектор
оцениваемых параметров. В данном случае
система уравнений (или одно уравнение
при оценке одного неизвестного
параметра распределения), получаемая
путем приравнивания к нулю первых
частных производных логарифмической
функции правдоподобия, не определена
или не имеет решений, в то время как
точка максимума существует. В подобных
ситуациях оценку следует искать другим
способом.
– оцениваемый параметр или вектор
оцениваемых параметров. В данном случае
система уравнений (или одно уравнение
при оценке одного неизвестного
параметра распределения), получаемая
путем приравнивания к нулю первых
частных производных логарифмической
функции правдоподобия, не определена
или не имеет решений, в то время как
точка максимума существует. В подобных
ситуациях оценку следует искать другим
способом.
Запишем функцию правдоподобия для равномерного распределения:
 ,
если
,
если
![]() ;
;
![]() –в
противном случае.
–в
противном случае.
Условие,
что все наблюдения принадлежат отрезку,
можно выразить через неравенства для
крайних членов вариационного ряда:
![]() ,
,![]() .
При фиксированнома
функция правдоподобия убывает по b
при
.
При фиксированнома
функция правдоподобия убывает по b
при
![]() и, следовательно, принимает максимальное
значение при
и, следовательно, принимает максимальное
значение при![]() .
При фиксированномb
функция правдоподобия возрастает по а
при
.
При фиксированномb
функция правдоподобия возрастает по а
при
![]() и, следовательно, принимает максимальное
значение при
и, следовательно, принимает максимальное
значение при![]() .
Таким образом, оценками максимального
правдоподобия будут
.
Таким образом, оценками максимального
правдоподобия будут![]() ,
,![]() .
.
Пример
10. Построить
оценку методом максимального правдоподобия
параметра сдвига ![]() для распределения Лапласа, заданного
плотностью
для распределения Лапласа, заданного
плотностью  ,
,
![]() .
.
Решение. Функция правдоподобия имеет вид
 .
.
Логарифмируя,
получаем
 .
.
Заметим,
что эта функция не дифференцируема во
всех точках
![]() ,
а в остальных точках производная имеет
вид:
,
а в остальных точках производная имеет
вид:

Отсюда
следует, что функция правдоподобия
возрастает, если слева от ![]() находится меньше членов вариационного
ряда, чем справа, и убывает – в противном
случае. Следовательно, максимума она
достигает посередине вариационного
ряда. Если
находится меньше членов вариационного
ряда, чем справа, и убывает – в противном
случае. Следовательно, максимума она
достигает посередине вариационного
ряда. Если ![]() ,
то это происходит в точке
,
то это происходит в точке ![]() .
Если
.
Если ![]() ,
то функция постоянна в интервале
,
то функция постоянна в интервале ![]() ,
где принимает наибольшее значение,
и в качестве оценки можно взять середину
этого интервала. Таким образом,
оценкой максимального правдоподобия
оказывается выборочная медиана:
,
где принимает наибольшее значение,
и в качестве оценки можно взять середину
этого интервала. Таким образом,
оценкой максимального правдоподобия
оказывается выборочная медиана:
![]() .
.
Пример
11. Найти
оценку параметра ![]() распределения
Пуассона методом наименьших квадратов.
распределения
Пуассона методом наименьших квадратов.
Решение.Найдем точку
минимума функции  :
:
 ;
;
Из
уравнения ![]() находим критическую
точку:
находим критическую
точку:
 ,
,
т.е.
 ,
,
 ,
,
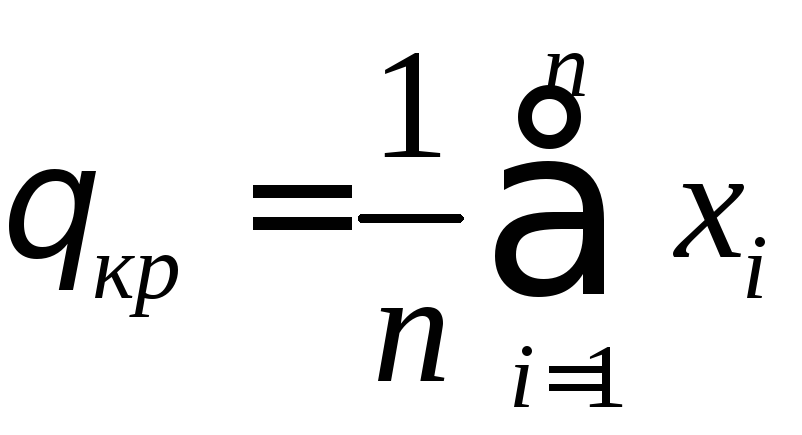 .
.
А так как
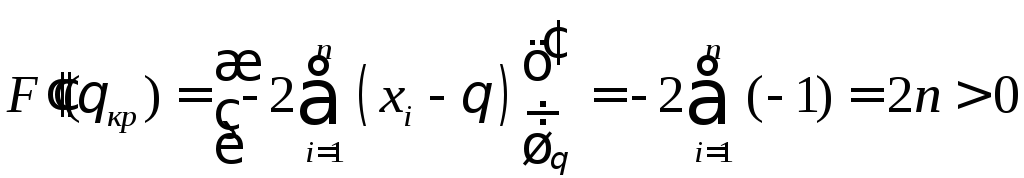
при
любом значении ![]() ,
то
,
то  – точка минимума функции
– точка минимума функции ![]() .
.
Таким
образом, оценкой параметра ![]() в распределении
Пуассона
в распределении
Пуассона  ,
,
![]() согласно МНК,
является
согласно МНК,
является 
Можно доказать, что:
![]()

