Модуль 2. Линейная регрессия. Элементы корреляционного анализа

Одной из основных задач математической статистики является исследование зависимости между двумя или несколькими переменными. Строгая функциональная зависимость реали­зуется редко, так как одна или обе величины подвержены еще и случайным факторам. Статистической называется зависи­мость, при которой изменение одной из величин влечет за собой изменение распределения другой. Основная цель изуче­ния зависимостей между случайными величинами заключается в прогнозировании с данной вероятностью области изменения одной случайной величины на основании наблюдаемых значе­ний другой случайной величины. На практике при исследова­нии зависимости между случайными величинами Х и Y часто ог­раничиваются исследованием зависимости между Х и условным математическим ожиданием . Функция называется функцией регрессии первого рода или модельной функцией регрессии Y на X, а график ее – линией рег­рессии.

Линейной регрессией называется сведение наблюдаемой на опыте зависимости некоторой переменной (зависимой или объясняемой) от одной или более других переменных (независимых или объясняющих) к линейной зависимости (в предположении, что строгая линейная зависимость между ними нарушается случай­ными ошибками). Для проведения линейной регрессии часто ис­пользуется метод наименьших квадратов.

В простейшем случае речь идет о двух переменных. Пусть х – независимая переменная, у – зависимая и между ними сущес­твует следующая связь:  где a и b – числовые коэффициенты, – случайные ошибки. Задача состоит в том, чтобы по имеющимся на­блюдениям ..., построить оценки для a и b. Согласно методу наименьших квадратов необходимо решить следующую математическую задачу:

Решаем задачу, вычисляя частные производные суммы квадратов по каждому из коэффициентов и приравнивая эти произ­водные к нулю. Получаем систему нормальных уравнений, которая позволяет получить оценки параметров а и b:

Уравнение вида называется уравнением линейной регрессии, а получаемые из него значения называют­ся предсказанными значениями, в отличие от наблюдаемых значе­ний y_i . Важным и практически значимым результатом линейной регрессии является то, что она позволяет «предсказывать» значения зависимой переменной даже для таких значений независимых, которые реально не наблюдались. Таким образом, например, можно строить прогнозы на будущее.

На практике часто бывает важно знать, существует ли зависимость между некоторыми наблюдаемыми величинами, и если да, то какая она — сильная или слабая, положительная или отри­цательная. Для выяснения этих обстоятельств используется кор­реляционный анализ.

Выборочным коэффициентом корреляции для выборки вида ..., называется выборочная характеристика

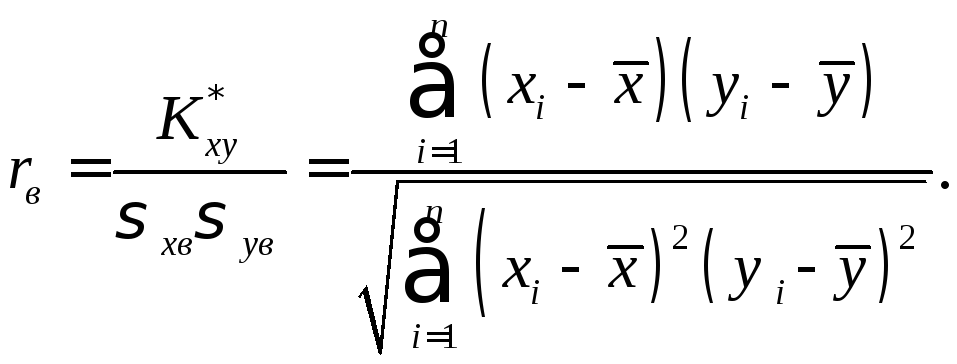
Отметим основные свойства коэффициента корреляции:

1. Выборочный коэффициент корреляции может принимать значения от – 1 до + 1. В зависимости от того, насколько приближается к 1, различают связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную, т.е. чем ближе к 1, тем теснее связь.

2. Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно и то же число раз, то величина коэффициента корреляции не изменится.

3. При корреляционная связь представляет линейную функциональ­ную зависимостъ.

4. При r = 0 линейная корреляционная связь отсутствует.

Таким образом, по абсолютной величине и знаку коэффициента можно судить о степени зависимости (сильной или слабой) и о ее характере (положительной или отрица-тельной).

В том случае, когда варианты парной выборки встречаются по нескольку раз, причём с одним значением варианты x_i может встретиться несколько вариант , их обычно представляют в виде корреляционной таблицы. На пересечении строк и столбцов этой таблицы отмечается частота выбора соответствующей парыа частоты вариантнаходятся как суммы значенийпо соответствующей строке или столбцу. Например, в корреляционной таблице

xi yj	10	20	30
5	3	–	2	5
10	5	4	2	11
	8	4	4	n = 16

пара (10; 5) встречается 3 раза, т.е. а частота появления величинынаходится как суммаОчевидно, что

Для коэффициента корреляции случайных величин X и Y в случае сгруппированных данных используется выражение

После подсчёта и получают выборочное уравнение линейной регрессии Y на X в виде

или выборочное уравнение линейной регрессии X на Y в виде

Для упрощения расчетов часто используются условные варианты, которые подсчитываются по формулам

где С₁, С₂ – ложные нули (выбираемые значения); h₁, h₂ – разности между соседними значениями X и Y.

Соответственно, для обратного перехода применяются выражения

где – средние значения условных вариант;средние квадратичные отклонения условных вариант.

Для подсчёта выборочного коэффициента корреляции в этом случае используются формула

Подсчитав выборочный коэффициент корреляции через условные варианты и осуществив переход к первоначальным переменным, получаем соответствующие уравнения регрессии.

Выборочный коэффициент корреляции обычно использует­ся в предположении нормальности данных. Как известно, в этом случае из равенства нулю теоретического коэффициента следу­ет независимость случайных величин (в более общем случае это неверно). В случае нормального распределения можно проверить гипотезу . Пусть

Если гипотеза верна, то Т имеет распределение Стьюдента с п – 2 степенями свободы. При уровне значимости выберем критическую точку  =  (; п – 2) для двусторонней области. Если | Т | < , то гипотеза принимается, иначе – отвергается.

В случае, когда нормальность данных нарушается, приме­нение выборочного коэффициента корреляции может вести к ошибкам: либо мы «не заметим» зависимость между величина­ми, либо получим ложную корреляцию. Существуют коэффици­енты и методы, свободные от предположения о нормальности.

Наблюдения всегда можно упорядочить по возрастанию какой-либо переменной (х или у). Рангом наблюдения называет­ся его номер в таком ряду. Если какое-то значение переменной встречается несколько раз, ему приписывается средний ранг. Обозначим ранги наблюдений по возрастанию х и у через r_i, и s_i соответственно. Пусть

Коэффициентом ранговой корреляции Спирмена называется величина

Этот коэффициент также может принимать значения от – 1 до + 1. Аналогичным образом он отражает силу и характер зависимости между величинами. Для проверки гипотезы о незави­симости случайных величин существуют специальные таблицы критических точек. Однако при больших п можно проверять гипотезу так же, как для обычного выборочного коэффициента корреляции.

Заметим, что с помощью коэффициента Спирмена можно анализировать также ситуации, когда некоторый признак объек­та («качество», «привлекательность» и т.п.) нельзя строго выра­зить численно, но можно упорядочить объекты по его возраста­нию или убыванию, т.е. проранжировать их.