Вопросы для самоконтроля

1. В чем различие между функциональной и статистической зависимостью двух переменных?

2. Какие основные задачи корреляционного анализа и регрессионного анализа?

3. Что называется функцией регрессии? Что понимают под регрессионной моделью?

4. В чем состоит сущность метода наименьших квадратов при подборе параметров модели регрессии?

5. По каким формулам определяются МНК-оценки коэффициентов двумерной регрессионной модели?

6. При каких предположениях данных используется выборочный коэффициент корреляции?

7. Существуют коэффициенты корреляции, свободные от предположения о нормальности данных?

8. Дать определение коэффициента ранговой корреляции Спирмана.

9. Какие значения может принимать коэффициента ранговой корреляции Спирмана?

10. Что отражает коэффициента ранговой корреляции Спирмана?

11. По какой формуле рассчитывается выборочный парный коэффициент корреляции ?

12. Перечислить основные свойства выборочного парного коэффициента корреляции.

13. Пусть . Что можно сказать о связи между признаками?

14. Пусть . Что можно сказать о связи между признаками?

15. Какой критерии применяется для проверки гипотез относительно коэффициента корреляции генеральной совокупности?

Образцы решения типовых задач

Пример 1.Найти коэффициент корреляции между произво-дительностью трудаY(тыс. руб.) и энерговооруженностью трудаX (кВт) (в расчете на одного работающего) для 14 предприятий региона по следующим данным, представленным в таблице

xi	2,8	2,2	3,0	3,5	3,2	3,7	4,0	4,8	6,0	5,4	5,2	5,4	6,0	9,0
yi	6,7	6.9	7.2	7.3	8,4	8,8	9,1	9,8	10.6	10,7	11,1	11,8	12,1	12,4

Решение. Вычислим необходимые суммы:

= 2,8 + 2,2 + ... + 6,0 + 9,0 = 64,2;

= 2,8² + 2,2² +... + 6,0² + 9,0² = 335,26;

 = 6,7 + 6,9 +... + 12,1 + 12,4 = 132,9;

 = 6,7² + 6,9² +... + 12,1² + 12,4²  = 1313,95;

 = 2,8 ∙ 6,7 + 2,2 · 6,9 +...+ 6,0 · 42,1 + 9,0 ∙ 12,4 = 650,99.

Получим

,

что говорит о тесной связи между переменными.

Этот пример можно решить, используя статистическую функцию в MS Excel КОРРЕЛ. Для этого необходимо:

1. Сформировать таблицу исходных данных:

2. Выбрать ячейку, в которую будет помещен результат.

3. Перейти на вкладку Формулы–Другие функции–Статистические и в раскрывающемся списке выбрать КОРРЕЛ.

4. В появившемся окне функции в качестве Массива1 выбрать диапазон значений x_i (B1:O1), а в качестве Массива2 выбрать диапазон значений y_i (B2:O2):

5. Полученный результат полностью совпадает с значением, вычисленным вручную (≈0,898).

Пример 2. Найти выборочный коэффициент корреляции по данным корреляционной таблицы

X Y	10	20	30
5	3	–	2	5
10	5	4	2	11
	8	4	4

Решение. Найдем оценки числовых параметров распре-деления. Вычисляем выборочные средние:

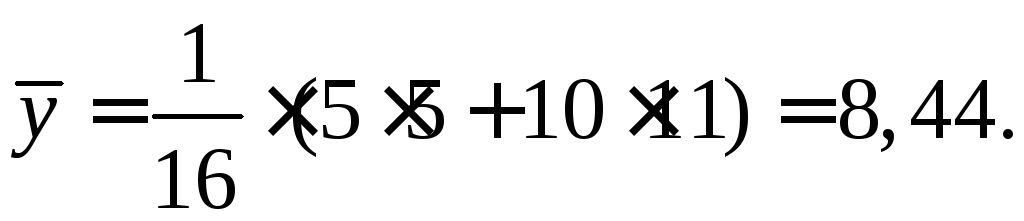
Несмещенные выборочные дисперсии:

Выборочные средние квадратичные отклонения:

Выборочный корреляционный момент:

.

Таким образом, выборочный коэффициент корреляции равен:

Выборочный коэффициент корреляции приближается к нулю, полому зависимость между случайными величинами не является линейной, она мо­жет быть выражена какой-либо иной зависимостью.

Пример 3. Из двухмерной нормальной генеральной совокупности извлечена выборка объемом n = 122. Найден выборочный коэффициент корреляции r_в = 0,4. Проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при уровне значимости и конкурирующей гипотезе Н₁.

Решение. Находим

По условию конкурирующая гипотеза Н₁: , поэтому критическая область – двусторонняя. По уровню значимости и числу степеней свободы 122 – 2 = 120 находим из таблицы 3 критических точек распределения Стьюдента для двусторонней критической областиt_кр =  (0,05, 120) = 1,98.

Так как Т_набл > t_кр, (4,79 > 1,98), то нулевую гипотезу отвергаем, т.е. выборочный коэффициент значимо отличается от нуля, следовательно, X и Y коррелируемы.

Пример 4. В таблице представлены средние цены на расти­тельное масло и сахар-песок (в руб.) в 12 городах Центрального района России на июнь 1996 года.

Город	Цена на масло	Цена на сахар
Брянск	7726	3410
Владимир	7880	3183
Иваново	6182	3209
Калуга	8237	3400
Кострома	8750	3600
Москва	11024	4418
Орел	8456	3634
Рязань	9172	4033
Смоленск	8320	3909
Тверь	7083	3416
Тула	8259	3486
Ярославль	7991	3938

Вычислить выборочный коэффициент корреляции между ценами на растительное масло и сахар. Проверить нулевую гипотезу на уровне значимости .

Решение. Выборочный коэффициент корреляции оказывает­ся равным r = 0,82. Имеем

,

в то время как (0,1; 10) = 1,81. Таким образом, нулевая гипотеза отвергается. Связь между ценами на растительное масло и сахар оказывается довольно сильной и положительной.

Пример 5. Знания десяти студентов проверены по двум тестам: А и В. Оценки по стобалльной системе оказались следующими (в первой строке указано количество баллов по тесту А, а во второй – по тесту В):

95 90 86 84 75 70 62 60 57 50

92 93 83 80 55 60 45 72 62 70

Найти выборочный коэффициент ранговой корреляции Спирмена между оценками по двум тестам.

Решение. Присвоим ранги r_i оценкам по тесту А. Эти оценки расположены в убывающем порядке, поэтому их ранги r_i равны порядковым номерам:

Ранги r_i 1 2 3 4 5 6 7 8 9 10

оценки по тесту A 95 90 86 84 75 70 62 60 57 50

Присвоим ранги оценкам по тесту В, для чего сначала рас­положим эти оценки в убывающем порядке и пронумеруем их:

1	2	3	4	5	6	7	8	9	10
93	92	83	80	72	70	62	60	55	45

Напомним, что индекс i при у должен быть равен порядковому номеру оценки студента по тесту А.

Найдем ранг s₁. Индекс i = 1 указывает, что рассматривается оценка студента, который занимает по тесту А в ряду первое место (эта оценка равна 95); из условия видно, что по тесту В студент получил оценку 92, которая расположена в ряду на второй месте. Таким образом, ранг s₁ = 2.

Найдем ранг . Индекс i = 2 указывает, что рассмат-ривается оценка студента, который занимает по тесту А в ряду второе место; из условия видно, что студент получил по тесту В оценку 93, которая расположена в ряду на первом месте. Таким образом, ранг .

Аналогично найдем остальные ранги: = 3,  = 4,  = 9, = 8, = 10, = 5, = 7, = 6.

Выпишем последовательности рангов r_i и s_i:

r_i 1 2 3 4 5 6 7 8 9 10

s_i 2 1 3 4 9 8 10 5 7 6

Найдем разности рангов: ; . Аналогично получим остальные разности рангов: 0, 0, – 4, – 2, – 3, 3, 2, 4. Вычислим сумму квадратов разностей рангов:

= 1 + 1 + 16 + 4+9 + 9 + 4+16 = 60.

Найдем искомый коэффициент ранговой корреляции Спирмена учитывая, что п = 10:

Решим эту задачу, используя инструменты MS Excel. Для этого:

1. Сформируем таблицу исходных данных:

2. Выберем ячейку С2 и перейдем на вкладку Формулы – Другие функции – Статистические и в раскрывающемся списке выберем функцию РАНГ.СР. В появившемся окне введем данные: Число – B2, Ссылка - $B$2:$B$11 (диапазон ранжируемых значений)

3. Снова выберем ячейку С2 и, зажав квадратик в нижнем правом углу ячейки, растянем формулы по столбцу до последнего значения. Все значения по тесту А будут проранжированы:

4. То же самое проделаем со столбцом Ранг по тесту B.

5. Теперь найдем разности рангов. В ячейку F2 введем функцию =D2-B2 и перенесем формулы по столбцу до последнего значения, как было сделано в п.3.

6. Посчитаем квадраты разности рангов. Для этого выберем ячейку G2 и перейдем на вкладку Формулы – Математические и в раскрывающемся списке выберем функцию СТЕПЕНЬ. В появившемся окне в поле Число вводим F2, в поле Степень – 2 и переносим формулы по столбцу до последнего значения.

7. Выделим диапазон G2:G11 и перейдя на вкладку Формулы выберем инструмент Автосумма:

8. Осталось посчитать коэффициент ранговой корреляции Спирмена по известной формуле. Для этого выберем ячейку G13 и введем в неё формулу: =1 – (6*G12/(1000-10)). По нажатию кнопки Enter в G13 появится значение ≈ 0,64.

Пример 6. Два контролера А и В расположили образцы изделий, изготовленных девятью мастерами, в порядке ухудшения качества (в скобках помещены порядковые номера изделий одинакового качества):

A 1 2 (3, 4, 5) (6, 7, 8, 9)

B 2 1 4 3 5 (6, 7) 8 9

Найти выборочный коэффициент ранговой корреляции Спирмена между рангами изделий, присвоенными им двумя контролерами.

Решение. Учитывая, что ранги изделий одинакового качества равны среднему арифметическому порядковых номеров изделий: (3 + 4 + 5)/3 = 4, (6 + 7 + 8 + 9)/4 = 7,5, (6+7)/2 = 6,5, напишем последовательности рангов, присвоенные изделиям контролерами:

r_i 1 2 4 4 4 7,5 7,5 7,5 7,5

s_i 2 1 4 3 5 6,5 6,5 8 9

Найдем выборочный коэффициент ранговой корреляции Спирмена, учитывая, что n = 9.

Пример 7. Преподавателю и студенту было предложено рас­положить 10 профессий в порядке их общественной значимости. От­веты перечислены ниже.

Оценка преподавателя	Профессии		Оценка студента
3	профессор		2
1	врач		1
4	учитель школы		7
2	директор магазина		4
8	бухгалтер		5
6	банкир		3
9	водитель		9
5	журналист		8
10	ди-джей		10
7	программист	6

Какова корреляция рангов между двумя рядами оценок? Одина­ково ли мнение преподавателя и студента по этому вопросу?

Решение. Определим разности рангов, их квадраты и суммы:

	1	0	–3	–2	3	3	0	–3	0	1
	1	0	9	4	9	9	0	9	0	1

Имеем:

Проверим, существует ли положительная корреляционная связь между мнениями преподавателя и студента. Для этого используем t­-статистику Студента с степенями свободы

.

Нулевая гипотеза – коэффициент корреляции не является статистической значимой . Альтернативная гипотеза –существует положительная корреляционная зависимость .

При уровне значимости для односторонней (правосторонней) критической области:

2,8264 > 1,86.

Следовательно, связь между мнениями преподавателя и студента является статистически значимой при 5% -ном уровне значимости.

Пример 8. Два эксперта проранжировали 11 фирм в порядке их привлекательности для инвестиций. Получены следующие последовательности рангов фирм:

	1	2	3	4	5	6	7	8	9	10	11
	1	2	3	5	4	9	8	11	6	7	10

Проверить, насколько согласуются мнения экспертов, с по­мощью коэффициента Спирмена. Проверить нулевую гипотезу на уровне значимости .

Решение. Вычисляем

1² + 1² + 3² + 1² + 3² + + 3² + 3² + 1² = 40,

отсюда

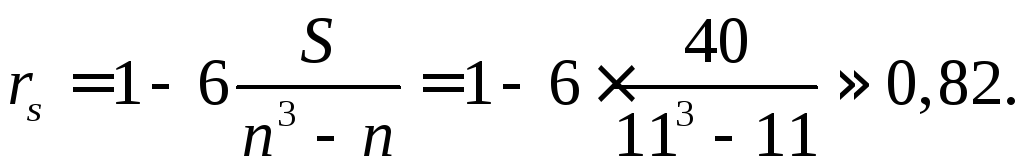
Для проверки нулевой гипотезы вычисляем

и (0,05; 9) = 2,26,

так что нулевая гипотеза отвергается. Мнения экспертов достаточно хорошо со­гласуются между собой.

Пример 9. Вычислить выборочный коэффициент коре-ляции и построить линейные регрессионные модели но данным корреляционной табли­цы

Y X	12,5	22,5	32,5	42,5	52,5	6,5
30	5	7	–	–	–	–
40	–	20	23	–	–	–
50	–	–	30	47	2	–
60	–	–	10	11	20	6
70	–	–	–	9	7	3

Решение. Для определения выборочных характеристик подсчитаем час­тоты появления значений случайных величин X и Y и представим их отдель­ными таблицами

X	12,5	22,5	32,5	42,5	52,5	62,5
	5	27	63	67	29	9

Найдем выборочное среднее для X:

Найдем выборочную дисперсию и выборочное среднее квадратичное отклоне­ние:

Аналогичные вычисления выполним и для величины Y.

Y	30	40	50	60	70
	12	43	79	47	19

Для нахождения выборочного корреляционного момента вычислим сумму:

Окончательно получаем:

Следует отметить, что близость выборочного коэффициента корреля­ции по модулю к единице является серьезным аргументом в пользу выбора линейной регрессионной модели.

Подставляем найденные выборочные характеристики в уравнение ли­нейной регрессии Y на X ):

Таким же образом находим уравнение линейной регрессии X на Y:

Если построить обе прямые регрессии на одном графике, то они пересекутся в точке с координатами .

Выборочный коэффициент корреляции по модулю приближается к единице, поэтому угол между прямыми линиями – острый.

Пример 10. Имеются следующие выборочные данные о стоимости квартир и общей их площади в городе.

Y	13,8	13,8	14	22,5	24	28	32	20,9	22	21,5	32	35	24	37,9	27,5
Х	33	40	36	60	55	80	95	70	48	53	95	75	63	112	70

Х – общая площадь квартиры, кв. м; Y – рыночная стоимость квартиры, тыс. у. е. Требуется:

1.  Построить график зависимости между переменными, по которому необходимо подобрать модель уравнения регрессии.

2.  Рассчитать параметры уравнения регрессии методом наименьших квадратов.

Решение. 1. График зависимости переменных X и Y строится в прямоугольной системе координат. На оси абсцисс откладываются значения факторного признака X, а по оси ординат – результативного признака Y. Учитывая небольшое число пар значений переменных, по каждой из них выделим пять интервалов, используя формулу: где h – длина интервала, k –  число интервалов. Для переменной X: Длина интервала округляется в сторону увеличения до удобного значения, h = 16. В результате получим следующие границы интервалов: 33+16=49; 49+16=65; 65+16=81; 81+16=97; 97+16=113.

Аналогично, для переменной Y: h = 4,82; h = 5. Границы интервалов составят: 13; 18; 23; 28; 33; 38.

На график накосятся точки, координаты которых соответствуют значениям X и Y.

Характер расположения точек на графике показывает, что связь между переменными может выражаться линейным уравнением рег­рессии

3.  Параметры уравнения регрессии находим методом наименьших квадратов, путем составления и решения системы нормальных урав­нений

Для проведения всех расчетов строится вспомогательная таблица

№	х	у			ху
1	33	13,8	1089	190,44	455,4
2	40	13,8	1600	190,44	552
3	36	14	1296	196	504
4	60	22,5	3600	506,25	1350
5	55	24	3025	576	1320
6	80	28	6400	784	2240
7	95	32	9025	1024	3040.
8	70	20,9	4900	436,81	1463
9	48	22	2304	484	1056
10	53	21,5	2809	462,25	1139,5
11	95	32	9025	1024	3040
12	75	35	5625	1225,1	2625
13	63	24	3969	576	1512
14	112	37.9	12544	1436.41	4244,8
15	70	27,5	4900	756,25	1925
Итого	985	368,9	72111	9867,85	26466,7
Среднее значе­ние	65,667	24,593	4807,4	657,857	1764,447

Учитывая, что п = 15; параметры уравнения регрессии также можно найти по форму­лам, вытекающим из системы нормальных уравнений.

Таким образом, уравнение регрессии имеет вид

4,7743 + 0,3018x.

Коэффициент регрессии показывает, что при увеличении общей площади квартиры на 1 м² стоимость квартиры в среднем увеличива­ется на 0,3018 тыс. у.е., или на 301,8 у.е.

Этот пример легко решить с помощью инструментов MS Excel. Для этого необходимо выполнить следующие действия:

1. Сформировать таблицу исходных данных:

2. Выбрать диапазон значений величин X и Y (B1:P2) и перейти на вкладку Вставка, в окне выбора диаграмм выбрать точечную. На экране появится график.

3. Нажав на поле диаграммы, в верхней части окна появятся две новые вкладки (КОНСТРУКТОР и ФОРМАТ) под заголовком РАБОТА С ДИАГРАММАМИ. Выбрать вкладку КОНСТРУКТОР и перейти к инструменту Добавить элементы диаграммы. В появившемся окне выбрать Линия тренда и в раскрывающемся списке выбрать Дополнительные параметры линии тренда.

4. После проделанных действии в правом углу появится окно Формат линии тренда. В этом окне выбираем тип линии тренда – Линейная, и отмечаем необходимость отображения на диаграмме уравнения регрессии и величины достоверности:

5. Для нахождения параметров регрессии методом наименьших квадратов воспользуемся статистической функцией ЛИНЕЙН.

6. Для этого выберем диапазон ячеек из двух столбцов и пяти строк (А4:В4) и перейдем на вкладку Формулы – Другие функции – Статистические и в раскрывающемся списке выбрать ЛИНЕЙН.

7. В поле Известные_значения_y вводим диапазон значений B2:P2, в поле Известные_значения_x вводим диапазон значений В1:Р1, в поля Конст и Статистика вводим ИСТИНА:

8. После введения данных нажимаем сочетание клавиш Ctrl+Shift+Enter для представления вычисления в виде массива данных, иначе отобразится только коэффициент b. Результат будет представлен в следующем виде:

b

a

Пример 11. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты X и числа уволившихся за год рабочих Y:

X	100	150	200	250	300
Y	60	35	20	20	15

Найти линейную регрессию Y на X и выборочный коэффициент корреляции.

Решение. Составим расчётную таблицу:

i	xi	yi
1	100	60	10000	6000	3600
2	150	35	22500	5250	1225
3	200	20	40000	4000	400
4	250	20	62500	5000	400
5	300	15	90000	4500	225
	1000	150	225000	24750	5850

Определяем коэффициенты a и b:

Выборочное уравнение регрессии примет вид

Из расчетной таблице следует, что

Находим выборочный корреляционный момент

Найдём по формулам

Откуда

Таким образом,

Пример 12. В магазине постельных принадлежностей в течение пяти дней подсчитывали число покупок простыней X и подушек Y:

xi	10	20	25	28	30
yi	4	8	7	12	14

Найти выборочное уравнение линейной регрессии Y на X и выборочный коэффициент корреляции.

Решение. Составим таблицу подсчётов.

Номер опыта i
1 2 3 4 5	10 20 25 28 30	4 8 7 12 14	100 400 625 784 900	40 160 175 336 420	16 64 49 144 196
	113	45	2809	1131	469

Находим a и b :

Уравнение регрессии запишется в виде

Подсчитаем корреляционный момент:

Находим

Определим выборочную дисперсию величин X и Y:

Откуда

Пример 13. Найти выборочное уравнение линейной регрессии X на Y на основании корреляционной таблицы

X Y	15	20	25	30	35	40
100	2	1	–	7	–	–
120	4	–	2	–	–	3
140	–	5	–	10	5	2
160	–	–	3	1	2	3

Решение. Для упрощения расчётов введём условные варианты

и составим преобразованную корреляционную таблицу с услов-ными вариантами, в которую внесём значения и:

U V	–3	–2	–1	0	1	2
–1	2	1	–	7	–	–	10
0	4	–	2	–	–	3	9
1	–	5	–	10	5	2	22
2	–	–	3	1	2	3	9
	6	6	5	18	7	8	n = 50

Затем составим новую Таблицу. Произведение частоты на варианту u, т.е. и записывают в правом верхнем углу клетки, содержащей значение частоты. Например, в правых верхних углах клеток первой строки записаны произведения:

Складывают все числа, помещенные в правых верхних углах клеток одной строки, и их сумму помещают в клетку этой же строки «столбца U». Например, для первой строки

Умножают варианту V на U и полученное произведение записывают в соответствующую клетку «столбца U». Например, в первой строке таблицы следовательно,

Сложив все числа «столбца U», получают сумму , которая равна сумме Например, в нашем случае

Для контроля, аналогичные вычисления производят по столбцам. Произведение записывают в левый нижний угол клетки, содержащий значение частоты: все числа, помещенные в левых нижних углах клеток одного столбца, складывают и их сумму помещают в «строку V»; умножают каждую варианту u на V и результат записывают в клетках последней строки.

X Y	–3	–2	–1	0	1	2
–1	–6 2 –2	–2 1 –1	–	0 7 –7	–	–	–8	8
0	–12 4 0	–	–2 2 0	–	–	6 3 0	–8	0
1	–	–10 5 5	–	0 10 10	5 5 5	4 2 2	–1	–1
2	–	–	–3 3 6	0 1 2	2 2 4	6 3 6	5	10
	–2	4	6	5	9	8	–
	6	–8	–6	0	9	16		–

Сложив все числа, последние строки получают сумму , которая также равна искомой сумме

Находим и :

Находим :

Определяем :

Вычисляем выборочный коэффициент корреляции :

Осуществляем переход к исходным вариантам:

Находим уравнение регрессии X на Y:

или

Пример 14. Найти выборочное уравнение линейной регрессии Y на X на основании корреляционной таблицы.

Y	X						ny
	10	20	30	40	50	60
15 25 35 45 55	5 – – – –	7 20 – – –	– 23 30 10 –	– – 47 11 9	– – 2 20 7	– – – 6 3	12 43 79 47 19
nx	5	27	63	67	29	9	n = 200

Решение. Введём условные варианты:

Для подсчёта можно использовать преобразованные корреляционные таблицы. Вначале составляем таблицу, в которой запишем условные варианты (C₁ = 40, C₂ = 35).

v	u						nv
	–3	–2	–1	0	1	2
–2 –1 0 1 2	5 – – – –	7 20 – – –	– 23 30 10 –	– – 47 11 9	– – 2 20 7	– – – 6 3	12 43 79 47 19
nu	5	27	63	67	29	9	n = 200

После этого составим таблицу, по которой найдем .

v	u
	–3	–2	–1	0	1	2
–2	–15 5 –10	–14 7 –14	–	–	–	–	–29	58
–1	–	–40 20 –20	–23 23 –23	–	–	–	–63	63
0	–	–30 30 0	–	0 47 0	2 2 0	–	–28	0
1	–	–	–10 10 10	0 11 11	20 20 20	12 6 6	22	22
2	–	–	–	0 9 18	7 7 14	5 3 6	13	26
	–10	–34	–13	29	34	12	–
	30	68	13	0	34	24		–

Таким образом,

Находим также и :

По формулам определяем средние квадратичные отклонения:

Подставляем рассчитанные данные в формулу для :

Затем рассчитываем по формулам

Получаем

Подставляем полученные значения в уравнение регрессии:

окончательно получаем

Пример 15. В результате измерений отклонений от номиналов высот моделей (х_i) и отливок к ним (у_j) получены следующие результаты:

хi	0,9	1,22	1,32	0,77	1,3	1,2	1,32	0,95	0,45	1,3	1,2
yi	–0,3	0,1	0,7	–0,3	0,25	0,02	0,37	–0,7	0,55	0,35	0,32

Cоставить корреляционную таблицу и вычислить коэффициент корреляции.

Решение. Разобьем весь интервал, в котором заключены значения признаков, на пять частей. Возьмем для х_i наименьшее значение 0,40 и наибольшее – 1,40, тогда ширина одного интервала будет равна 0,20. Наименьшее y_j = –0,7, а наибольшее – 0,7. Ширина интервала 0,28. Откладываем интервалы изменений х_i по горизонтали, а у_j – по вертикали; данные заносим в таблицу

X Y	0,4– 0,6	0,6– 0,8	0,8 – 1	1 – 1,2	1,2– 1,4	ny
– 0,7…  – 0,42 – 0,42…  – 0,14 – 0,14 – 0,14 0,14 – 0,42 0,42 – 0,7	– – – – 1	– 1 – – –	1 1 – – –	– – – 2 –	– 1 1 2 1	1 3 1 4 2
nx	1	1	2	2	5	n = 11

Определим коэффициент корреляции. Для этого найдем средние значения и , предполагая, что х_i и у_j – середины соответствующих интервалов:

,

Коэффициент корреляции  = 0,82 близок к единице, следовательно, между случайными величинами Х и Y достаточно тесная корреляционная связь.

Пример 16. Распределение 40 заводов области по количеству Y ремонтных слесарей и числу X станкосмен представлено следующей корреляционной таблицей

Y X	10– 15	15– 20	20– 25	25– 30	30– 35	35– 40	nx
0 – 0,2 0,2 – 0,4 0,4 – 0,6 0,6 – 0,8 0,8 – 1,0 1,0 – 1,2	4 2 – – – –	– 2 – 6 – –	– – 2 – – –	– – – 4 – –	– – – 4 6 –	– – – – 6 4	4 4 2 14 12 4
ny	6	8	2	4	10	10	n = 40

Составить уравнение прямой регрессии Y на X, установить тесноту связи между признаками. Для каждого интервала значений Y вычислить фактические значения частных средних и теоретические значения, найденные из уравнений регрессии.

Решение. За значения признаков примем середины интервалов и составим корреляционную таблицу в условных вариантах, приняв в качестве условных нулей C₁ = 0,7 и C₂ = 27,5. (Эти варианты имеют частоту, равную 4, и находятся в середине корреляционной таблицы.)

V U	–3	–2	–1	0	1	2	nu
–3 –2 –1 0 1 2	4 2 – – – –	– 2 – 6 – –	– – 2 – – –	– – – 4 – –	– – – 4 6 –	– – – – 6 4	4 4 2 14 12 4
n	6	8	2	4	10	10	n = 40

Находим:

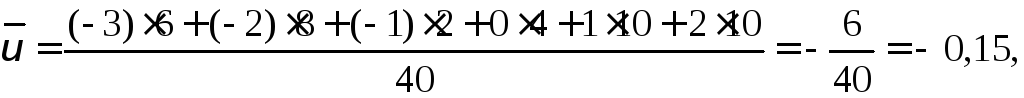
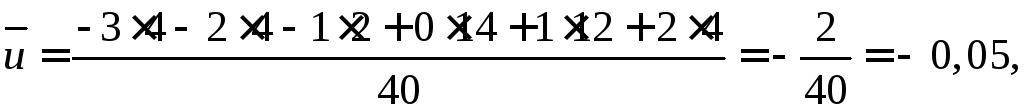
Найдем искомый коэффициент корреляции:

Вычислим :

Подставим полученные значения в уравнение регрессии:

или

Вычислим для каждого интервала изменения х фактические значения частных средних:

,

,,

, .

Вычислим для каждого интервала изменения х теоретические значения из полученного уравнения:

, ,

, ,

, .

Cравнивая полученные теоретические значения, видим, что они близки к фактическим.

Пример 17. Затраты х на развитие производства и у – величина годовой прибыли фирмы в течение пяти лет – представлены в ус­ловных единицах таблицей:

X	6	3	7	5	10
Y	33	27	32	28	42

На величину прибыли влияют случайные факторы. Предполагается, что имеет место линейная зависимость между затратами х и прибылью у. Каждый год случайное влияние не коррелировано с предыдущими годами. Оценить параметры а и b.

Оце­нить годовую прибыль в случае, если на развитие производства будет затрачено 12 у.е.

Решение. Перейдем к условным вариантам

, .

и	0	–3	1	–1	4
V	0	–6	–1	–5	9

Получаем = (0 – 3 + 1 – 1 + 4)/5 = 0,2;  = (0–6–1– –5+ 9)/5 = – 0,6. Отсюда = 6,2; = 32,4. Далее, вычисляем

= 18 – 1 + 5 + 36 + 0,6 = 58,6;

= 9 +1 + 1 + 16 – 0,2 = 26,8.

Получаем  = 58,6/26,8  2,187;  = 32,4 – 2,1876,2  18,843. Имеем (12) 45 у.е.