
1. Пл-ть комп. чисел.
опр. компл. числом z наз. выражение вида z=x+iy, где x,yR и i - мнимая единица.
опр. z=x+iy, тогда Re z=x - действит. часть, Jm z=y - мнимая часть z. зам. если Re z=0 - число чисто мнимое.
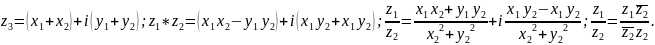
опр.
комп. число x-iy
наз. сопряженным к z=x+iy
и обозн.
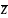 .
.
опр.
модулем. комп. числа наз. длина вектора
его изображ.
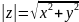 .
.
опр. аргументом наз. угол на кот. нужно повернуть положит. часть оси Ox до совпадения с вектором, изображ. комп. число z. Arg z.
опр.
гл. аргументом наз.
 и обозн. arg
z.
и обозн. arg
z.
Тригоном.
форма:
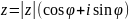 (
(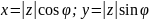 ).
).
св-ва
модулей:

св-ва
аргументов:
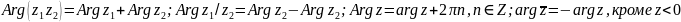 .
.
2. Предел пос-ти с комп. членами.
опр. задана посл-ть компл. чисел если каждому натур. числу по некот. правилу поставлено в соотв. единств. компл. число.
опр.
Комп. число а наз. пределом посл-ти zn
если
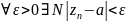 и обозн.
и обозн.
 .
.
опр.
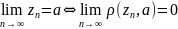 .
.
теор.
задана посл-ть zn=an+ibn.
Тогда
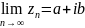 т и т т, когда
т и т т, когда
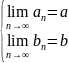
теор.
если
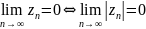 .
.
док-во:
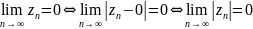
опр.
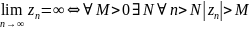 .
.
3. Числ. ряды с комп. членами.
опр.
числ. рядом наз. символ вида
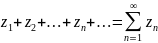 .
Члены посл-ти наз. членами ряда.
.
Члены посл-ти наз. членами ряда.
опр.
Сумма n
первых членов ряда наз. n-ой
част. суммой
 .
.
опр.
числ. ряд наз. сх-ся если сущ. конечный
предел посл-ти его част. сумм
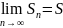 .
В противном случае - расходящимся.
.
В противном случае - расходящимся.
сх-ть числ. ряда эквивалентно сх-ти 2х числ. рядов с действит. членами, сост. из действит. и мнимой частей исх. ряда.
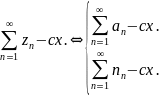
зам. числ. ряды комп. анализа обладают всеми привычными св-вами числовых рядов.
опр.
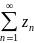 -
абс. сх-ся если сх-ся ряд из модулей
членов данного ряда.
-
абс. сх-ся если сх-ся ряд из модулей
членов данного ряда.
опр.
если
-
сх-ся, а
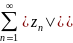 - не сх-ся, то сам ряд наз. условно
сходящимся.
- не сх-ся, то сам ряд наз. условно
сходящимся.
4. Функция комплексного переменного. опр. на мн-ве D задана ф-ция компл. перем. z если каждой т. мн-ва D по некот. правилу поставлено в соответствие одно или неск. компл. чисел w. w=f(z). При этом если z соотв. 1 число, то ф-цию наз. однозначной, в противном сл. - многозначной.
зам. задание ф-ции комп. переем. эквивалентно заданию 2х действ. ф-ций 2х переменных.
z=x+iy, w=f(x+iy)=U(x,y)+i*V(x,y); U(x,y)=Re f(z), V(x,y)=Jm f(z).
В отличии от ф-ций одной действ. переем., где принято изображать график на координатной пл-ти, для ф-ций компл. переем. принято откладывать знач. незав. переем. z на одной пл-ти, а знач. ф-ции на другой пл-ти. Ф-ция комп. переем. - отображение мн-ва D пл-ти z на мн-во E пл-ти w. Если разл. т. мн-ва D соотв. различные т. мн-ва E (биекция), то ф-ция наз. однолистной.
5. Линейная ф-ция. Ее геометрический смысл. Задана ф-ция w=az+b, abC - const, a0, D(w)=C.
1. a=1, w=z+b - ф-ция w осущ. параллельный перенос на радиус-вектор числа b.
2. a1 a. |a|=1; w=az+b; w-z0=a(z-z0), |w-z0|=|z-z0|; Arg(w-z0)=Arg(a)+Arg(z-z0); z0=b/(1-a);
лин. ф-ция задает поворот вокруг точки b/(1-a)на угол Arg(a).
b. |a|1, Arg(a)=0; w-z0=a(z-z0), z0=b/(1-a); |w-z0|=|a|*|z-z0|; Arg(w-z0)=Arg(z-z0);
Лин. ф-ция представляет собой гомотетию с центром в т. z0 и коэфф., равным |a|.
c. запишем a в тригонометрической форме: a=ρ(cosφ+isinφ)= ρτ; |ρ|=|a|, Arg(ρ)=0; |τ|=1, Arg(τ)= φ=Arg(a); w-z0=a(z-z0); w-z0= ρτ(z-z0); введем доп. ф-цию h= ρ(z-z0)+z0; w-z0= τ(h-z0); т.о. w явл. композицией гомотетии с центром в т z0 с коэфф. |a| и поворота вокруг т. z0 на угол Arg(a).
зам. Рассм. лин. ф-цию вида w-z0=a(z-z0)+c. Данная ф-ция это композиция гомотетии, поворота и парал. переноса, то есть явл. преобразованием подобия.
6. Предел и непрерывность ф-ции комп. переем. Ф-ция w=arg(z). Задана однозначная ф-ция w=f(z) в некот. окр. т. z0=x0+iy0.
Комп.
число bC
наз. пределом
ф-ции w=f(z)
в т. z0
если ε>0
δ>0
z0U(z0),
0<|z-z0|<
δ =>|f(z)-b|<
ε
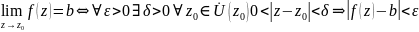
опред. предела связано с понятием расстояния, с метрич. простр-вом, все осн. св-ва предела переносятся на случай комп. перем. Но здесь рассм. толкьо 3 вида пределов, в кот. участвует беск. удаленная точка:
1.
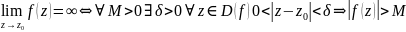
2.

3.
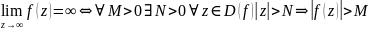
теор. задана т. z0=x0+iy0 и число b=b1+ib2 и в окр. т z0 опред. ф-ция f(z)=U(x,y)+iV(x,y). Тогда число b явл. пределом ф-ции f(z) в т. z0 тогда и только тогда когда ф-ции U(x,y) и V(x,y) имеют пределы в т. (x0,y0) равные b1 и b2 соответственно.
опр.
ф-ция f(z)
наз. непрерывной в т. z0
если
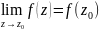 .
.
w=arg(z); D(w)=C/{0}; z0-x, x>0;
Возьмем
произв.ε>0;
δ=|z0|sinε;

7.
Понятие
производной ф-ции комп. перем.
Условия
Коши-Римана.
опр.
если сущ. конечный предел отношения
приращения ф-ции к приращению аргумента,
когда последний стремится к 0, то он наз.
производной ф-ции f(z)
в т. z0,
и обозн. f’(z)
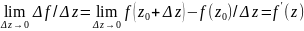 .
.
В комп. анализ переносятся все правила дифф-ния, теор. о произв. сложной и обратной ф-ции.
опр.
ф-ция w=f(z)
наз. дифф-мой в т z0
если ее приращение в этой т. можно
представить в виде:
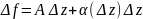 ,
где A
- const,
α-б/м
величина при Δz0.
(дифф-сть эквивалентна наличию произв.
ф-ции в т. z0,
причем A=f’(z0))
,
где A
- const,
α-б/м
величина при Δz0.
(дифф-сть эквивалентна наличию произв.
ф-ции в т. z0,
причем A=f’(z0))
теор. Условия Коши-Римана. Для того, что бы ф-ция f(z)=U(x,y)+iV(x,y) была дифф-ма в т. z0=x0+iy0 необх. и дост. чтобы ф-ции U(x,y) и V(x,y) были дифф-мы в т. (x0,y0) и их частн. произв. в т. (x0,y0) удов. условиям:
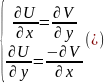
док-во:
1.необх. дано:f(z)-диф-ма
в т.z0.
док-ть:(*).
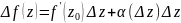 ,
обозн.
,
обозн.
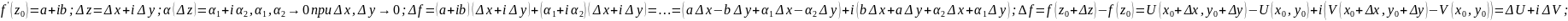
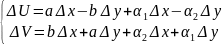 ,
отсюда вытекает, что ф-ция U
дифф-ма в т.
,
отсюда вытекает, что ф-ция U
дифф-ма в т.
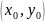 ,
причем
,
причем
 .
Аналогично ф-ция V
диф-ма в т.
.
Аналогично ф-ция V
диф-ма в т.
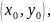
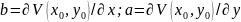 ,
т.о. следует (*).
,
т.о. следует (*).
2.дост.
дано:U,V-диф-мы.
док-ть:f(z)-диф-ма
в т.z0.
нужно показ. что сущ. произв. f’(z0).
т.к. U
и V
диф-мы в т.
,
то их приращ. можно предст. в виде:
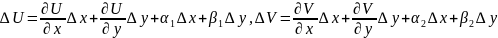 ,
где
,
где
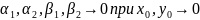 .
Сост. приращ. ф-ции f(z):
.
Сост. приращ. ф-ции f(z):
 .
.
8. Геом. смысл Модуля аргумента. Понятие конформного отображения.
Задана
ф-ция w=f(z)
имеющ. произв. в т. z0,
f’(z0)0.
Предп. что из т. z0
вых. кривая γ,
имею. касат. в т. z0.
Рассм. произв. т. zγ.
Тогда вектор
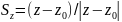 будет явл. еденичным секущим вектором.
|Sz|=1.
Arg
Sz=αz
т.к. в т. z0
суш. касат., то сущ.
будет явл. еденичным секущим вектором.
|Sz|=1.
Arg
Sz=αz
т.к. в т. z0
суш. касат., то сущ.
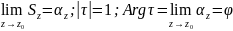 .
На пл-ти w:
.
На пл-ти w:
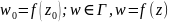 .
Рассм. вектор
.
Рассм. вектор
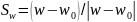 - ед. вектор секущей дял кривой Г.
Преобразуем
- ед. вектор секущей дял кривой Г.
Преобразуем
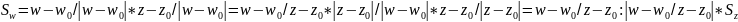 Перейдем к пределу при zz0
в Sw:
Перейдем к пределу при zz0
в Sw:
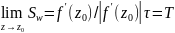 .
Т.о. в т. w0
кривая Г имеет касат. для кот. справедл.
соотношения:
.
Т.о. в т. w0
кривая Г имеет касат. для кот. справедл.
соотношения:
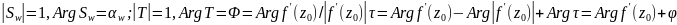 .
Получим рав-во:
.
Получим рав-во:
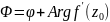 .
Т.о. при
отображ. f(z)
Arg
f’(z0)
представл. собой угол
поворота,
кот. совершает касат. к кривой. То есть
при отображ. f(z)
сохр. угол между кривыми.
.
Т.о. при
отображ. f(z)
Arg
f’(z0)
представл. собой угол
поворота,
кот. совершает касат. к кривой. То есть
при отображ. f(z)
сохр. угол между кривыми.
опр. отображение, сохраняющее углы, наз. конформным.
Геом.
смысл модуля произв.:
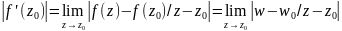 ,
т.о. |f’(z0)|
- коэфф.
деформации
(растяжения или сжатия) отображ. f(z)
в т. z0.
,
т.о. |f’(z0)|
- коэфф.
деформации
(растяжения или сжатия) отображ. f(z)
в т. z0.
9. Показательная ф-ция и ее св-ва. Опред. ф-цию w=ez след. образом: ez=ex+iy=ex(cosy+isiny). (если Jm(z)=0, z=x, то ez=ex).
Осн.
св-ва: 1.
| ez|=
ex;
2.
если Re(z)=0,
z=iy,
то ez=cosy+isiny
(ф-ла Эйлера); 3.
ez
явл. аналитичной во всей комп. пл-ти,
причем (ez)’=
ez;
4.
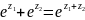 ,док-во:
,док-во:
 ;
5.
ф-ция ez
явл. периодической с периодом T0=2πi;
6.
ф-ция w=ez
осущ. конформное отображение комп.
пл-ти;
;
5.
ф-ция ez
явл. периодической с периодом T0=2πi;
6.
ф-ция w=ez
осущ. конформное отображение комп.
пл-ти;
10. Логарифмическая ф-ция. опр. число w наз. натуральным логарифмом комп. числа z если ew=z и обозначается w=Ln z.
теор.
любое, отличное от нуля, комп. число z
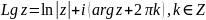 .
.
док-во:
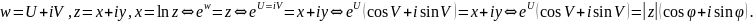
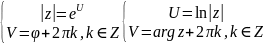
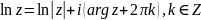 ,
что и
требовалось доказать.
,
что и
требовалось доказать.
св-ва:
1.
w=Ln
z
явл. многозначной. 2.

опр.
главным логарифмом наз. значение
логарифма опред. по формуле
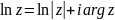 .
.
св-ва
главного логарифма:
1.
Гл. логарифм определен
 .
2.
Гл. логарифм явл. непрерывной ф-цией на
всей комп. пл-ти с разрезом вдоль отриц.
действит. полуоси. 3.
Гл. логарифм явл. аналит. ф-цией во всей
комп. пл-ти с разрезом вдоль отриц.
действит. полуоси, причем производная
.
2.
Гл. логарифм явл. непрерывной ф-цией на
всей комп. пл-ти с разрезом вдоль отриц.
действит. полуоси. 3.
Гл. логарифм явл. аналит. ф-цией во всей
комп. пл-ти с разрезом вдоль отриц.
действит. полуоси, причем производная
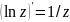 .
.
11.
Тригонометрические
ф-ции. синус
комп. числа z
опред. по формуле:
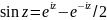 ;
;
косинус
комп. числа z
оред. по формуле:
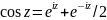 ;
;
зам.
данные определения естественны (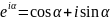 ).
).
Осн.
св-ва: 1.
cos
- четная ф-ция, sin
- нечетная ф-ция. 2.
sin
и cos
явл. периодическими с периодом 2π.
3.
Для sin
и cos
сохр. все привычные тригоном. тождества
(как
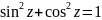 ).
4.
sin
и cos
явл. аналит. во всей комп. пл-ти. 5.
sin
и cos
явл. неограниченными.
).
4.
sin
и cos
явл. аналит. во всей комп. пл-ти. 5.
sin
и cos
явл. неограниченными.
опр.
гиперб. косинусом наз. величина
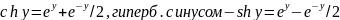 .
.
6.

12. Интеграл от ф-ции комп. перем. Условия его сущ.
На
пл-ти комп. перем. задана спрямляемая
кривая Г и вдоль этйо кривой определена
ф-ция w=f(z).
Разобьем Г точками z0,…,Zn
на част. дуги и выберем на каждой из них
точку ck,
k=1,…,n.
Составим след. сумму
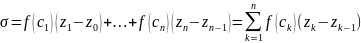 .
.
опр.
Сумма вида σ
наз. интегр. суммой для w=f(z)
на кривой Г соотв. данному разбиению
кривой на част. дуги и выбору т. ck.
Обозн. наиб из длин
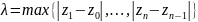 .
.
опр.
если сущ. конечный предел инегр. сумм σ
при λ0,
то его наз. интегралом от f(z)
по кривой Г и обозн.
 .
.
теор. если Г - гладкая кривая на пл-ти комп. перем., а f(z) - непрерывна на Г, то сущ интеграл .
док-во:
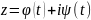 - ур-ние Г,
- ур-ние Г,
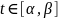 .
Разобъем кривую Г т. z0,...,zn
на част. дуги. Выберем на каждой из них
т. ck,
k=1,…,n.
И пусть на Г задана непр. ф-ция
.
Разобъем кривую Г т. z0,...,zn
на част. дуги. Выберем на каждой из них
т. ck,
k=1,…,n.
И пусть на Г задана непр. ф-ция
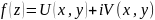 .
Введем обозн.:
.
Введем обозн.:
 .
Сост. интегр. сумму
.
Сост. интегр. сумму
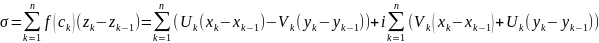 ;
Введем обозн.:
;
Введем обозн.:
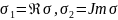 .
Заметим, что
.
Заметим, что
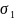 - интегр. сумма для ф-ции
- интегр. сумма для ф-ции
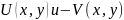 вдоль кривой Г, а
вдоль кривой Г, а
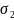 - для
- для
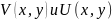 .
Т.к. f(z)
непрер-на вдоль Г, то непрерывны и
.
Т.к. f(z)
непрер-на вдоль Г, то непрерывны и
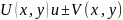 ,
а значит по теор. о сущ. криволин. интегр.
2 рода сущ. пределы:
,
а значит по теор. о сущ. криволин. интегр.
2 рода сущ. пределы:
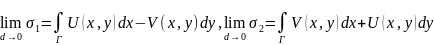 ,
d
- диаметр разбиения Г на част. дуги. Т.к.
,
d
- диаметр разбиения Г на част. дуги. Т.к.
 .
.
зам. из док-ва видно, что вычисл. интегр. от ф-ции комп. перем. сводится к вычисл. 2х криволин. интегр. 2 рода.
зам.:
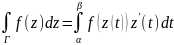 .
.
13. Интегральная теор. Коши.
теор.
Коши:
Пусть ф-ция f(z)
аналитична в односвязной обл. D
конечной пл-ти и Г -замкн. спрямл. аривая
целиком лежащая в D.
Тогда
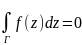 .
.
опр. D - наз. односвязной если любая кусочно-гладкая простая замкн. кривая целиком лежаая в D ограничивает обл., все точки кот. принадлежат D. зам. односвязнйо наз. обл. если ее граница состоит из одной простой замкн. кривой. опр. обл. наз. n-связной (многосв.) если ее граница состоит из n замкн. кривых, не имеющих общих точек.
док-во:
при условии, что f’(z)
непрерывна в D,
f(z)=U(x,y)+iV(x,y)
т.к. f(z)
аналит., то ф-ции U(x,y)
и V(x,y)
- дифф-мые.
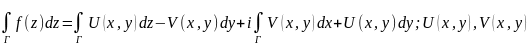 - непрерывны, то дял каждого криволин.
интегр. справедлива формула Грина:
- непрерывны, то дял каждого криволин.
интегр. справедлива формула Грина:
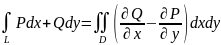 .
.
 ,
в силу аналитичности f(z),
для нее вып. все условия Коши-Римана:
,
в силу аналитичности f(z),
для нее вып. все условия Коши-Римана:
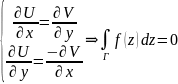 ,
что и требовалось док-ть.
,
что и требовалось док-ть.
зам.
теор. Коши остается в силе и в случае
многосвязной обл-ти при условии, что
кривая Г огрна. обл. целиком сост. из т.
D.
Сл.1:
если Г1
и Г2
спрямл. кривые целиком лежащие в обл. D
аналитичности f(z)
имеющие общий конец и начало, то
 ,
интеграл не зависит от пути интегрирования.
Сл.2:
f(z)
аналит. в двусвязной обл. D,
границей кот. явл. кривые Г и γ.
Тогда
,
интеграл не зависит от пути интегрирования.
Сл.2:
f(z)
аналит. в двусвязной обл. D,
границей кот. явл. кривые Г и γ.
Тогда
 .
.
14. Первооброзная. Формула Ньютона-Лейбница.
теор. если f(z) аналитична в обл. D то F(z) так же аналитична в D, причем справедливо равенство F’(z)=f(z) zD.
опр.: ф-ция Ф(z) наз. первообразной для f(z) если она аналитична в обл. D и справедливо р-во: Ф’(z)=f(z) zD.
Вспомогат.
фундам.
теор.:
 .
.
док-во:
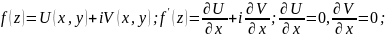
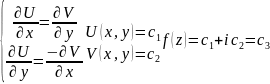
теор.: Если F(z) и Ф(z) явл. первообразными для f(z)в обл. D, то Ф(z)=F(z)+c, c=const.
ф-ла
Ньютона-Лейбница:
Г - произв. кривая с началом в т. z1
и концов в т z2
и f(z)
аналитична в некот. обл. D
содержащей Г. Тогда:
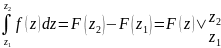 .
.
15. Интегральная формула Коши.
Теор.
Пусть ф-ция f(z)
аналитична в односвязн. обл. D
и на ее границе Г, тогда aD
справеливо
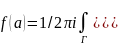 .
.
док-во:
рассм. произв. aD.
Выберем произв. ε>0,
т.к. f(z)
аналит. в т. a,
то и непрерывна в ней, тогда ε>0
δ>0
zD
|z-a|<δ
=> |f(z)-f(a)|<ε.
Рассм. круг с ц. в т. a
радиуса r<δ,
K(a,r)
и обозн. его границу Г. Рассм. ф-цию
f(z)/z-a
- аналит. в обл. D,
за искл. т. a,
а значит аналит. в двусвязн. обл., получ.
из D
исключением круга K(a,r).
Тогда по следств. из теор. Коши:
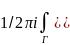 .
Покажем, что он равен f(a):
.
Покажем, что он равен f(a):
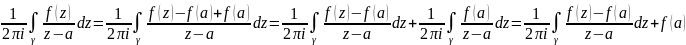 ;
Покажем, что первое слагаемое = 0
;
Покажем, что первое слагаемое = 0
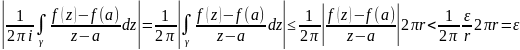
зам.
если ф-ция аналит. в D
и на ее границе, то она однозн. опред.
через свои знач. на границе Г:
 .
.
зам.
если т. a
лежит во внешности контура Г, то
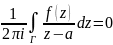 .
.
16. Ф-циональный ряд в комп. пл-ти. Равномерная сходимость.
опр.
ф-циональным рядом наз. символ вида
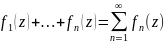 .
опр.
n-ой
част. суммой ф-ного ряда наз ф-ция
.
опр.
n-ой
част. суммой ф-ного ряда наз ф-ция
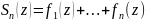 .
Рассм. произв.
т. z0D.
Тогда ф-цион. рду ставится в соотв.
числовой ряд, если он сх-ся, то т. z0
наз. т. сходимости.
опр.
мн-во Е всех т. сх-ти ряда наз. обл-тью
сх-ти ф-ного ряда. опр.
ф-ция S(z)
опред. на мн-ве Е для кот. Sn(z)=S(z)
zD
наз. суммой ф-ного ряда. опр.
ф-ный ряд наз. равномерно сх-ся на мн-ве
М если вып. условия: 1.
S(z)
сх-ся на М. 2.
.
Рассм. произв.
т. z0D.
Тогда ф-цион. рду ставится в соотв.
числовой ряд, если он сх-ся, то т. z0
наз. т. сходимости.
опр.
мн-во Е всех т. сх-ти ряда наз. обл-тью
сх-ти ф-ного ряда. опр.
ф-ция S(z)
опред. на мн-ве Е для кот. Sn(z)=S(z)
zD
наз. суммой ф-ного ряда. опр.
ф-ный ряд наз. равномерно сх-ся на мн-ве
М если вып. условия: 1.
S(z)
сх-ся на М. 2.
 .
.
теор.
ф-ный ряд сх-ся равномерно к S(z)
на мн-ве М т и т т, когда
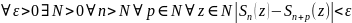 .
.
теор.
Признак
Вейерштрасса.
Пусть ряд
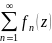 ,
тогда zМ
сущ. сх-ся знакоположит. ряд
,
тогда zМ
сущ. сх-ся знакоположит. ряд
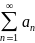 такой, что |fn(z)|<an,
тогда данный ф-ный ряд сх-ся равномерно
на мн-ве М.
такой, что |fn(z)|<an,
тогда данный ф-ный ряд сх-ся равномерно
на мн-ве М.
св-ва равн. сх-ся рядов: теор. если ряд сх-ся равн. на М и ф-ция fn(z) непрерывна на М, то сумма этого ряда явл. непрерывной ф-цией на М.
Лемма:
пусть ф-ный ряд сх-ся равн. на спрямляемой
кривой Г и каждая fn(z)
непр-на на Г, тогда этот ряд можно почленно
интег-вать вдоль кривой Г:
 .
.
теор.
ф-ный ряд рав-но сх-ся в обл. D
и ф-ции fn(z)
аналит. в этой обл., тогда сумма ряда
S(z)
так же аналит. в обл. D,
причем
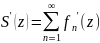 .
.
