17. Степенные ряды.

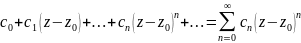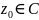опр. степ. рядом наз. ф-ным рядом вида , где c₀,…,c_n - компл. числа наз. коэфф., - центр ряда.

теор. Абеля. если ряд 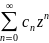сх-ся в т. z₀, то он сх-ся во всех т. z кот. удовлетв. нер-ву |z|<|z₀|.

сл.: если ряд расх-ся в некот. т. z₀, то он расходится во всех т., удовл. условию |z|>|z₀|.

Из теор. Абеля следует, что RR, |z|<R - сх-ся, а при |z|>R - расх-ся. R - радиус сходимости. .

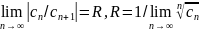св-ва: 1. степ. ряд явл. аналит. ф-цией. 2. сумма ряда - непрерывная ф-ция. 3. ряд м.б. продефф-ван и проинтегрирован любое число раз, причем радиус сходимости не меняется.

опр. если ф-ция f(z) явл. суммой ряда , то этот ряд явл. рядом Тейлора, причем его коэфф. опред. по формуле

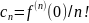
сл.: ф-ция f(z) явл. суммой ряда , то этот ряд наз. рядом Тейлора с центром в т. а с коэфф.

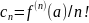
18. Аналитическая ф-ция. Разложение в ряд.

опр. ф-ция f(z) наз. аналитической в т. z₀ если она дифф-ма в каждой т. некот. окрестности т. z₀.

зам. аналит. в т. z₀ ф-ция будет аналитической в каждой т. некот. окр. т. z₀.

опр. ф-ция наз аналитической на мн-ве D если она аналитична в каждой т. этого мн-ва.

теор.: если ф-ция аналитична в круге с ц. в т. a, то она представима в виде степенного ряда. .

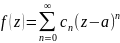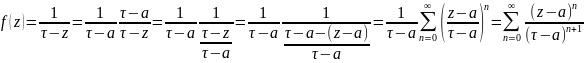(круг с ц. в т. а радиуса τ).

док-во: Выберем т. z, нарисуем круг с ц. в т. a, включающий т. z. Применим теор. Коши: 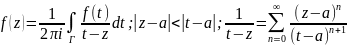подставляя это в f(z) получим: 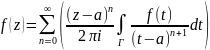. 2 следствия:

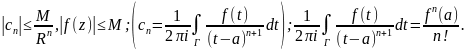
19. Теорема единственности.

опр. т. а наз. предельной т. мн-ва Е если в любой ее окр. содержится хотя бы 1, отличная от а, точка мн-ва Е.

л емма: если f(z) аналитична в откр. круге |z-a|<r и обращ. в ноль на мн-ве Е этого круга, имеющеи пред. т. а, то f(z)=0 во всех т. этого круга.

теор. единственности: Пусть 2 ф-ции f₁(z) и f₂(z) аналит. в D и приним. одинаковые знач. на мн-ве Е, имеющем хотя бы 1 пред. т. Тогда эти ф-ции совпадают всюду в обл. D.

док-во: а - пред. т. Е, рассм. ф-цию f(z)=f₁(z)-f₂(z) и покажем, что они тожд. равна 0 в обл. D. Построим круг U₀ с ц. в т. а радиуса r₀, так, чтобы U₀D. По лемме: в круге U₀ f(z)=0 zU₀. Рассм. произв. т. zD, т.к. D - связное мн-во, то соединим а и z непр. кривой, целиком лежащей в обл. D. Рассм. произв. т. а внутри U₀. Построим U₁: |z-a|<r₁, U₁D, т.к. а₁ - пред. т., то по лемме в U₁ f(z)=0 zU₁. Рассм. т. а₂γ, а₂U₁, рисуем U₂ и т.д. Продолжаем рисовать пока круг не накроет т. z. В последнем круге f(z)=0 по лемме, и в т. z ф-ция тоже равна нулю. В силу произв. т. z f(z)=0 zD. Значит ф-ция f₁(z) и f₂(z) равны всюду в обл. D.

20. Аналитическое продолжение.

Аналитическое продолжение - расширение обл. опред. аналит. ф-ции с сохранением её аналитичности.

Простейшим примером может служить переход от ф-ций действит. перем. к ф-циям компл. перем., аналит. во всей (или почти во всей) пл-ти и совпадающим с соотв. ф-циями действ. перем. при действ. знач. аргумента.

Для многих спец. ф-ций аналит. продолжение осущ.с пом. нек. ф-ного ур-ния. Берется нек. обл., в кот. решение этого ур-ния заведомо аналит., и осущ. перенос результатов на большую область. В основном таким способом строятся прод. спец. ф-ций вещ. анализа — например, гамма-функции и дзета-функции Римана.

опр. лакунарная ф-ция - ф-ция, аналит. в круге сх-ти собств. ряда Тейлора, но кот. не может быть продолжена аналит. куда-либо за пределы этого круга.

теор. Адамара: ф-ция 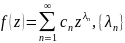- возр. посл-ть натур. чисел. Тогда, если 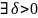такая, что 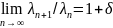, то ф-ция f(z) будет лакунарной.

21. Теорема Лиувилля.

Если f(z) аналит. во всей комп. пл-ти С и огрна. в ней, то она постоянна.

док-во: т.к. f(z) аналитична в C, то ее можно представить в виде ряда, то f(z)=c₀+c₁z+c₂z²+… т.к. f(z) ограничена., M>0 zC |f(z)|M. Рассм. произв. окр. γ: |z|=r с ц. в 0 радиуса r, тогда в силу нерав-в Коши будем иметь 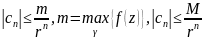. Устремим 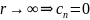за искл. .

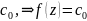22. Нули аналит. ф-ции.

опр. комп. число а наз. нулем ф-ции f(z) если f(a)=0. опр. ноль а ф-ции f(z) наз. изолир. если сущ. окр. т. а в кот. нет других нулей этой ф-ции.

теор1. f(z) отличная от тождеств. нуля аналитичная в обл. D может иметь в этой обл. только изолир. нули.

док-во: предположим противное: аналит. ф-ция имеет неизолир. ноль - а. То есть в любой окр. т. а есть по крайней мере еще один ноль. Обозначим мн-во этих нулей E  D, а - пред. т. Е. f(z)=0 zD, значит она ноль во всей обл.

теор2. если т. а явл. нулем аналит. ф-ции f(z) отличной от тождеств. константы, то сущ. такое натур. число n, что в некот. окр. т. а справедливо рав-во 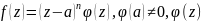- аналитична. (где n - порядок нуля ф-ции).

теор3. а явл. нулем порядка n ф-ции f(z) аналит. в т. а т и т т, когда .
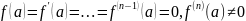