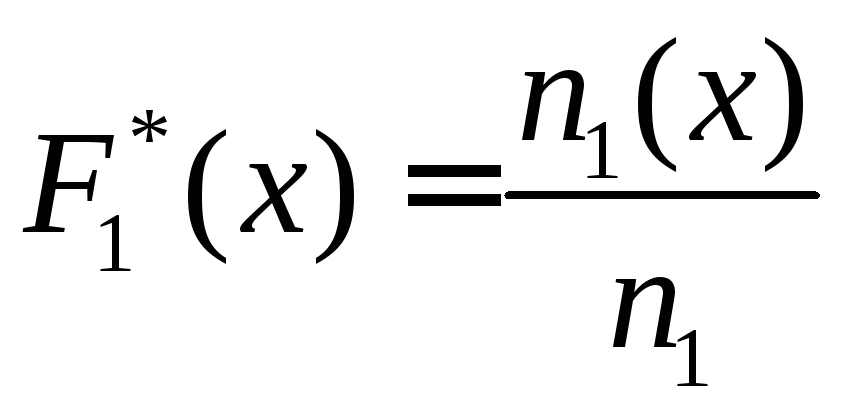Вопросы для самоконтроля

1. Дать определение статистической гипотезы.

2. Какие гипотезы называются параметрическими (непара-метрическими) гипотезами?

3. Дать определение нулевой (основной) гипотезы. Как она обозначается?

4. Дать определение альтернативной (конкурирующей) гипотезы. Как она обозначается?

5. Дать определение простой гипотезы. Привести пример.

6. Дать определение сложной гипотезы. Привести пример.

7. Что такое статистический критерий?

8. Дать определение наблюдаемого значения статисти-ческого критерия.

9. Дать определение критической области.

10.Что называется областью принятия гипотезы?

11. В чем состоит односторонность действия статистических критериев значимости?

12. Можно ли, применяя статистический критерий значимости, сделать вывод: «Проверяемая нулевая гипотеза верна»?

13. Дать определение критических точек (квантилей).

14. Каким неравенством задается правосторонняя крити-ческая область?

15. Каким неравенством задается левосторонняя крити-ческая область?

16. Какими неравенствами задается двусторонняя крити-ческая область?

17. В чем состоит различие между построением двусто-ронней критической области и построением доверительного интервала для одного и того же параметра?

18. Что такое ошибки первого рода?

19. Что такое ошибка второго рода?

20. Как изменяются вероятности совершения ошибки первого и второго рода при увеличении объема выборки?

21. Зависят ли вероятности совершения ошибок первого и второго рода от вида альтернативной гипотезы, от применяемого критерия?

22. Что такое критерий согласия? Для чего он исполь-зуется?

23. С чем связан критерий Колмогорова? Верно ли, что при его использовании сравниваются эмпирическая и предполагаемая функции распределения?

24. Когда в принципе возможно применение критерия Колмогорова?

25. С чем связан критерий Пирсона?

26. Верно ли, что для применения критерия Пирсона необходимо, чтобы в каждом интервале вариационного ряда было по крайней мере 5 наблюдений?

Образцы решения типовых задач

Следующие типы гипотез проверяются для нормальных данных: .

Пример 1. Из нормальной генеральной совокупности с из­вестным средним квадратическим отклонением извлечена выборка объемап = 100, и по ней найдено выборочное среднее 26,5. Требуется на уровне значимости 0,05 проверить гипотезу против альтернативной гипотезы . Изме­нится ли результат, если заменить альтернативную гипотезу на ?

Решение. Найдем значение статистики критерия

При проверке гипотезы из соотношения находим и , так что основная ги­потеза отвергается. В данном случае имеет место двусторонняя критическая область. При проверке гипотезы с учетом односторонней критической области, из соотно­шения находим и , так что основная гипотеза отвергается. В обоих случаях результат одинаков.

Пример 2. По выборке объема п = 16, извлеченной из нормаль­ной генеральной совокупности, найдены выборочное среднее, равное 12,4, и исправленное среднее квадратическое отклоне­ние, равное 1,2. Требуется при уровне значимости 0,05 прове­рить нулевую гипотезу при конкурирующей гипотезе

Решение. Найдем наблюдаемое значение статистики крите­рия

Поскольку конкурирующая гипотеза имеет вид то искомая критическая область двусторонняя. Из таблицы 3 критичес­ких точек распределения Стьюдента найдем по уровню значи­мости и числу степеней свобод критическую точку t_кр = 2,13. В силу того что , у нас нет оснований отвергнуть ну­левую гипотезу.

Пример 3. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900 часов. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 часов при выборочном среднем квадратичном отклонении 700 часов При 5%-м уровне значимости проверить гипотезу о том, что значение 2900 часов является математическим ожиданием.

Решение. Предположим, что случайная величина срока безотказной работы подчинена нормальному закону распределения. Требуется проверить гипотезу о числовом значении математического ожидания нормально распределенной величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию

,

где – выборочная средняя, – математическое ожидание, s – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с степенями свободы. В данной задаче речь идет о сравнении выборочной средней 2720 ч. с гипотетическим математическим ожиданием= 2900ч, при этом выборочное среднее квадратичное отклонение равно 700 ч.

Требуется найти критическую область для нулевой гипотезы при альтернативной гипотезе . Очевидно, что другие альтернативные гипотезы (и) нецелесообразны, т.к. потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком. Критическая область левосторонняя;находим из условия. При α = 0,05 и= 50–1 = 49 по таблице 3 критических точек распределения Стьюдента, используя криволинейную интерполяцию, находим . Таким образом, критическая область. РассчитаемT_набл :

Значение – 1,8 попадает в критическую область, поэтому нулевая гипотеза должна быть отвергнута. Следовательно, фирма в рекламе завышает срок безотказной работы изделия.

Пример 4. Точность работы станка-автомата проверяется по дисперсии размеров изделий, которая не должна превышать (мм²). По выборке из 25 изделий получена исправленная выборочная дисперсия s² = 0,02 (мм²). На уровне значимости 0,05 проверить, обеспечивает ли станок необходимую точность.

Решение. Найдем значение статистики критерия

По таблице 2 находим критическую точку распределения хи-квадрат с степенью свободы: .Поскольку 48 > 36,4, то основная гипотеза отвергается. Сле­довательно, станок не обеспечивает необходимой точности.

Пример 5. Из нормальной генеральной совокупности извле­чена выборка объема п = 31. В следующей таблице представлены сгруппированные данные.

Варианта	10,1	10,3	10,6	11,2	11,5	11,8	12,0
Частота	1	3	7	10	6	3	1

Требуется на уровне значимости 0,05 проверить нулевую ги­потезу , приняв в качестве конкурирующей гипотезы .

Решение. Перейдем к условным вариантам .

	–9	–7	–4	2	5	8	10
	1	3	7	10	6	3	1

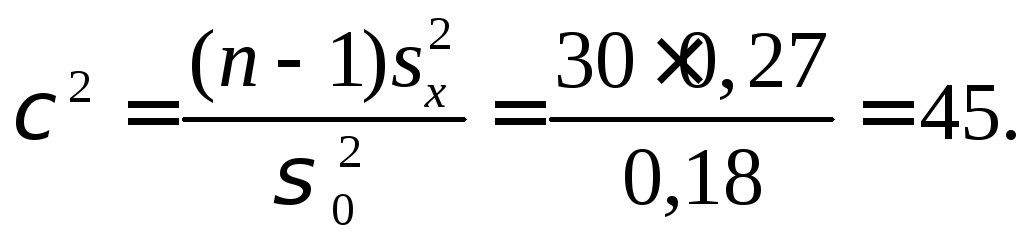
По таблице 2 критических точек распределения хи-квад-рат по уровню значимости и числу степеней свободы находим .Поскольку 45 > 43,8, основная гипотеза отвергается.

Пример 6. Партия изделий принимается, если доля брака со­ставляет не более 2 %. Среди случайно отобранных 500 изделий оказалось 13 бракованных. Следует ли принять партию (на уров­не значимости 0,05)?

Решение. Относительная частота брака составляет

Найдем значение статистики критерия

Из соотношения находим и_кр = 1,65 и получаем U_набл < и_кр, так что основная гипотеза принимается. Таким образом, партию изделий можно принять.

Пример 7. Торговец утверждает, что он получает заказы в сред­нем, по крайней мере, от 30 % предполагаемых клиентов. Мож­но ли при 5%-ном уровне значимости считать это утверждение неверным, если торговец получил заказы от 20 из 100 случайно отобранных потенциальных клиентов.

Решение. В данном случае нулевая гипотеза будет выглядеть как , а конкурирующая  – как .

Найдем значение статистики критерия, учтя, что относи­тельная частота для данной задачи равна =  20/100 = 0,2:

Из соотношения находим и_кр = 1,65 и U_набл < – и_кр, так что нулевая гипотеза отвергается, и с утверждением торговца мы не соглашаемся.

Пример 8. Имеются следующие данные об урожайности пшеницы на 8 опытных участках одинакового размера (ц/га): 26,5; 26,2; 35,9; 30,1; 32,3; 29,3; 26,1; 25,0. Есть основание предполагать, что значение урожайности третьего участка x^*=35,9 зарегистрировано неверно. Является ли это значение аномальным (резко выделяющимся) на 5%-ном уровне значимости?

Решение. Исключив значение x = 35,9, найдем для оставшихся наблюдений и. Фактически наблюдаемое значениебольше табличного, следовательно, значениеx = 35,9 является аномальным, и его следует отбросить.

Пример 9. В   молочном отделе универсама произведено контрольное взве­шивание десяти 200-граммовых пачек творога и установлено, что г и s = 4 г. Менеджер отдела выдвигает предположение о не­добросовестности поставщика. Прав ли он? Уровень значимости принять равным

Решение.  г (злоупотреблений нет). (т.к. 196 < 200) – левосторонняя критическая область. Для проверки гипотезы H₀ будем применять критерий

Вычислим T_набл  = . По таблице 3 критических  точек  распределения  Стьюдента найдем критическое значение критерия: t_кр = – 4,3. Следовательно, нет оснований отклонить нулевую гипотезу.

Пример 10. Менеджер банка решил внедрить единую систему обслуживания клиентов в порядке их входа в операционный зал и по мере освобождения операционистов. Хотя такая политика и не меняет среднее время ожидания для клиентов банка, менеджер отдает ей пред­почтение, так как считает, что она уменьшает вариацию времени ожида­ния. Оппоненты менеджера приводят доводы, что эта вариабельность будет, по крайней мере, больше, чем при прежней системе, когда клиент сам выбирал операциониста и становился к нему в одну из многих оче­редей. По опыту прошлых лет известно, что стандартное отклонение со­ставляет мин. на клиента. С целью установления истины руковод­ство банка решило проверить статистически, кто прав: менеджер или оппоненты. Проверка основывалась на случайной выборке 20 клиентов, на которых проверялась новая система обслуживания и которая показала, что исправленное среднее квадратическое отклонение равно 4 мин. на человека. Какой вывод сделали бы Вы на 5%-ном уровне значимости?

Решение. Сформулируем две гипотезы:

Имеем левостороннюю критическую область. Очевидно, что для проверки нулевой гипотезы банковский статистик предложил следующий критерий: . Вычислим  = 8,44. По таблице 2 критических точек распределения хи-квадрат найдем χ²_набл < χ²_кр.

Вывод: нулевая гипотеза должна быть отклонена, что означает: вы­борочный результат статистически значим, т. е. новая система более удобна для клиентов банка.

Пример 11. По выборке объема п = 30 найден средний вес изготовленных на первом станке изделий, равный 130 г; по выборке объeма m = 40 найден средний вес изготовленных на втором станке изделий, равный 125 г. Генеральные дисперсии известны: г², г². Требуется на уровне значимости 0,05 про­верить нулевую гипотезу  а_х = а_у при конкурирующей гипотезе H₁: а_х  а_у. Предполагается, что случайные величины распределе­ны нормально и выборки независимы.

Решение. Найдем значение статистики критерия

По таблице 1 функции Лапласа находим критическую точку из равенства . В результате получаем . Поскольку , то отвергается. Таким образом, нельзя утверждать, что средние значения веса изделий двух стан­ков совпадают.

Пример 12. По двум независимым извлеченным из нормаль­ных генеральных совокупностей выборкам, объемы которых п = 9 и т = 16, найдены исправленные выборочные дисперсии и . На уровне значимости 0,01 проверить нулевую гипотезу против конкури-рующей гипотезы .

Решение. Рассчитаем значение статистики критерия

Числа степеней свободы n – 1 = 8, т – 1 = 15. Из таб­лицы 4 критических точек распределения Фишера – Снедекора по заданному уровню значимости и числам степенейсвободы находим f_кр = 4. Поскольку F_набл <  f_кр, нулевая гипотеза принимается.

Пример 13. Реклама утверждает, что из двух типов пластиковых карт «Русский экспресс» и «Супер-понт» богатые люди предпо­читают первый. С целью проверки этого утверждения были об­следованы среднемесячные платежи п = 16 обладателей «Русского экспресса» и т = 11 – обладателей «Супер-понта». Выяснилось, что платежи по картам «Русский экспресс» составляют в среднем 563 долл. с исправленным средним квадратическим отклонени­ем 178 долл., а по картам «Супер-понт» – в среднем 485 долл. с исправленным средним квадратическим отклонением 196 долл.

Предварительный анализ законов распределения месячных расходов как среди обладателей «Русского экспресса», так и сре­ди обладателей «Супер-понта» показал, что они достаточно хо­рошо описываются нормальным приближением. Проверить утверждение рекламы на уровне значимости 10 %.

Решение. В данном случае следует проверить гипотезу о сред­них при неизвестных дисперсиях (объемы выборок малы). По­этому, прежде всего, необходимо проверить гипотезу о равенстве дисперсий, а лишь затем двигаться дальше.

Имеем

Из таблицы 4 критических точек распределения Фишера – Снедекора по уровню значимости и числам степенейсвободы п_тах – 1 = 10 и п_тin – 1 = 15 находим критичес­кую точку f_кр = 2,55. Поскольку 1,21 < 2,55, принимаем гипотезу о равенстве дисперсий двух выборок.

Теперь можно воспользоваться критерием Стьюдента для проверки гипотезы о равенстве средних.

Имеем

Вычисление статистики критерия дает

.

Из таблиц 3 критических точек распределения Стьюдента (для односторонней области) по уровню значимости и числустепеней свободы 25 находим t_кp = 1,32. Поскольку Т_набл < t_кp, то принимается основная гипотеза (о ра­венстве средних). Таким образом, утверждение рекламы не под­тверждается имеющимися данными.

Пример 14. В партии из 500 деталей, изготовленных первым станком-автоматом, оказалось 60 нестандартных, из 600 дета­лей второго станка – 42 нестандартных. На уровне значимости проверить нулевую гипотезу о равенстве веро­ятностей изготовления нестандартной детали обоими станками против конкурирующей гипотезы .

Решение. Имеем = 60/500 = 0,12; = 42/600 = 0,07; (60 + 42)/(500 + 600) .

Находим значение статистики критерия

Критическую точку находим их соотношения , откуда . Поскольку , то отвергается. Значит, вероятности изготовления нестандартных деталей на двух станках различны.

Пример 15. Срок хранения продукции, изготовленной по технологии А, составил:

Срок хранения,	5	6	7
Число единиц продукции,	2	4	4

а изготовленной по технологии В:

Срок хранения,	5	6	7	8
Число единиц продукции,	1	8	7	1

Предположив, что случайные величины X и Y распределены по нормальному закону, проверить гипотезу при уровне значимости 0,1 и альтернативной гипотезе.

Решение. Вычислим «исправленные» выборочные дисперсии , . Для этого вначале найдем,:

;      .

Тогда

;

.

Учитывая, что , определим.

По таблице 4 критических точек распределения Фишера находим с уровнем значимости и числами свободы и ; где – объем выборки с меньшей выборочной дисперсией, – с большей;

Так как число F_набл = 5,64 попадает в критическую область , то гипотезу о равенстве дисперсий среднего срока хранения продукции, изготовленной по технологиямА и В, отвергаем.

Пример 16. Средний ежедневный объем продаж за I квартал текущего года для 17 торговцев района А составляет 15 тыс. руб. при «исправленном» среднем квадратичном отклонении 2,5 тыс. руб., а для 10 торговцев района В – 13 тыс. руб. при «исправленном» среднем квадратичном отклонении 3 тыс. руб. Каждую группу можно считать случайной независимой выборкой из большой совокупности. Существенно ли различие объемов продаж в районах А и В при 5%-м уровне значимости?

Решение. Предположим, что ежедневный объем продаж подчинен нормальному закону распределения. Математическое ожидание и среднее квадратичное отклонение законов распределения для районов А и В неизвестны. Предположим, что дисперсии объемов продаж одинаковы. В этих условиях возникает задача оценки статистической гипотезы при альтернативной , если принять заa_x математическое ожидание объема продаж для района А, за a_y – для района В.

Выборочные средние иявляются независимыми нормально распределенными случайными величинами.

В этом случае в качестве критерия используют функцию

, где .

Функция Т подчинена t-распределению для степеней свободы.

По таблице 3 критических точек распределения Стьюдента для числа степеней свободы и 5%-го уровня значимости (для двусторонней критической области) находимt_кр = 2,06. Это значит, что критическая область есть интервал и.

Вычислим Т_набл:

,

Полученное значение критерия Т_набл не принадлежит критической области, следовательно, разность несущественна и гипотеза принимается. В качестве общей средней выборочной принимают величину

.

Пример 17. В условиях примера 16 выяснить, существенно ли при 5%-ном уровне значимости превышение объема продаж в районе А по сравнению с объемом в районе В.

Решение. Вопрос в данном примере отличается от вопроса в примере 16 тем что альтернативной к гипотезе становится не гипотеза, а гипотеза. В этом случае критическая область односторонняя, в частности, правосторонняя:. Так какТ_набл = 1,86 > 1,71, то величина Т_набл входит в критическую область, поэтому превышение объема продаж в районе А по сравнению с объемом в районе В существенно и гипотеза отвергается.

Пример 18. Фирма предлагает автоматы по розливу напитков. При выборке n = 16 найдена средняя величина  г дозы, наливаемой в стакан автоматом №1. По выборке m= 9 найдена средняя величина  г дозы, наливаемой в стакан автоматом №2. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальный закон распределения с дисперсией, равной  г². Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости α = 0,01?

Решение. Пусть a_x и a_y – математические ожидания доз, наливаемых автоматом №1 и автоматом №2. Нулевая гипотеза в данном случае при альтернативныхи. Дисперсия известна:. В качестве критерия справедливости статистической гипотезы выбирается функция

,

распределенная по нормальному закону с параметрами (0, 1).

1. Рассмотрим вначале гипотезу для альтерна-тивной. В этом случае критическая область имеет вид, гдеопределяется из условия. Откуда. Значит, левосторонняя критическая область будет.

Рассчитаем U_набл:

Полученное значение U_набл = – 1,44 не входит в критическую область , поэтому нулевая гипотеза принимается.

2. Рассмотрим гипотезу при альтернативной. В этом случае критическая область двусторонняя и имеет вид. При этом критическая точка выбирается из условия:

, .

Критическая область имеет вид . ЗначениеU_набл = –1,44 не попадает в критическую область, поэтому нулевая гипотеза принимается.

Пример 19. Для проверки эффективности новой технологии были отобраны две группы рабочих: в первой группе численностью  = 50 чел., где применялась новая технология, выборочная средняя выработка составила (изделий), во второй группе численностью = 70 чел. выборочная средняя – (изделий). Предварительно установлено, что дисперсии выработки в группах равны соответственнои. На уровне значимостиα = 0,05 выяснить влияние новой технологии на среднюю производительность.

Решение. Проверяемая гипотеза , т.е. средние выработки рабочих одинаковы по новой и старой технологиям. В качестве конкурирующей гипотезы можно взятьили(В данной задаче более естественна гипотеза, так как ее справедливость означает эффективность применения новой технологии). Фактическое значение статистики критерия

.

При конкурирующей гипотезе критическое значение статистики находится из условия , т.е., откуда= 2,58.

Так как фактически наблюдаемое значение  = 4 больше критического значения (при любой из взятых конкурирующих гипотез), то гипотеза отвергается, т.е. на 5%-ом уровне значимости можно сделать вывод, что новая технология позволяет повысить среднюю выработку рабочих.

Пример 20. Произведены две выборки урожая пшеницы: при своевременной уборке урожая и уборке с  некоторым опозданием. В первом случае при наблюдении 8 участков выборочная средняя урожайность составила 16,2 ц/га, а среднее квадратическое отклонение – 3,2 ц/га; во втором случае при наблюдении 9 участков те же характеристики равнялись соответственно 13,9 ц/га и 2,1 ц/га. На уровне значимости α = 0,05 выяснись влияние своевременной уборки урожая на среднее значение урожайности.

Решение. Проверяемая гипотеза , т.е. средние значения урожайности при своевременной уборке урожая и с некоторым опозданием равны. В качестве альтернативной гипотезы берем гипотезу, принятие которой означает существенное влияние на урожайность сроков уборки. Фактически наблюдаемое значение статистики критерия

,

где .

Критическое значение статистики для односторонней области определяется при числе степеней свободы и уровню значимости α = 0,05 по таблице 3 приложения. Находим,  = 1,75. Так как , то гипотеза принимается. Это означает, что имеющиеся выборочные данные на 5%-ом уровне значимости не позволяют считать, что некоторое запаздывание в сроках уборки оказывает существенное влияние на величину урожая. Еще раз подчеркнем, что это не означает безоговорочную верность гипотезы . Вполне возможно, что только незначительный объем выборки позволил принять эту гипотезу, а при увеличении объемов выборки (числа отобранных участков) гипотеза будет отвергнута.

Пример 21. На двух токарных станках обрабатываются втулки. Отобраны две пробы: из втулок, сделанных на первом станке  = 13 шт., на втором станке –  = 18 шт. По данным этих выборок рассчитаны выборочные дисперсии (для первого станка) и(для второго станка). Полагая, что размеры втулок подчиняются нормальному закону распределения, на уровне значимости α = 0,05 выяснить, можно ли считать, что станки обладают различной точностью.

Решение. Имеем нулевую гипотезу , т.е. дисперсии размера втулок, обрабатываемых на каждом станке, равны. Возьмем в качестве конкурирующей гипотезу(дисперсия больше для первого станка).

Число степеней свободы и из таблицы 4 приложения критических точек распределения Фишера на уровне значимости α = 0,05. Находим . Так как < f_кр, то гипотеза не отвергается, т.е. имеющиеся данные не позволяют считать, что станки обладают различной точностью.

Пример 22. Экзаменационный билет по математике содержит 10 заданий. Пусть Х – случайная величина числа задач, решенных студентами на экзамене. Результаты сдачи экзамена по математике для 300 студентов таковы:

i	1	2	3	4	5	6	7	8	9	10	11
xi	0	1	2	3	4	5	6	7	8	9	10
mi	13	17	15	35	10	9	40	51	45	33	32

Оценить закон распределения случайной величины Х.

Решение. Для составления гипотезы о модели закона распределения случайной величины Х сделаем следующие предположения:

1. вероятность решения задачи не зависит от исхода решения других задач;

2. вероятность решить любую отдельно взятую задачу одна и та же и равна p, а вероятность не решить задачу равна .

При этих допущениях можно предположить, что Х подчинена биномиальному закону распределения (нулевая гипотеза), т.е. вероятность того, что студент решит x задач, может быть подсчитана по формуле

.

Найдем оценку параметра p, входящего в модель.

Здесь p – это вероятность того, что студент решит задачу. Оценкой вероятности p является относительная частота p^*, которая вычисляется по формуле

,

где – среднее число задач, решенных одним студентом;v – число задач, решаемое каждым студентом.

Тогда оценку для p получим в виде

При p^* = 0,6 и q^* = 1 – 0,6 = 0,4 при различных x_i получим теоретические вероятности и теоретические частоты. Представим расчеты в виде таблицы

Номер группы i	xi
1	0	0,0001	0,03
2	1	0,0016	0,48
3	2	0,0106	3,18
4	3	0,0425	12,75
5	4	0,1115	33,45
6	5	0,2007	60,21
7	6	0,2508	75,24
8	7	0,2150	64,50
9	8	0,1209	36,27
10	9	0,0403	12,09
11	10	0,0060	1,80

Из таблицы видно, что для групп 1, 2, 3 и 11 теоретическая частота . Такие группы обычно объединяются с соседними. Это представляется естественным, потому что за 0, 1, 2 и 3 решенные задачи на экзамене обычно ставится неудовлетворительная оценка. Объединим так же группу 11 с группой 10 и составим таблицу.

Номер группы i	1	2	3	4	5	6	7
xi	0 – 3	4	5	6	7	8	9 – 10
mi	80	10	9	40	51	45	65
	16	33	60	75	64	36	14

По данным этой таблицы рассчитываем величину критерия согласия Пирсона:

.

Зададимся уровнем значимости , тогда для степеней свободы.

Величина , следовательно, нулевая гипотеза должна быть отвергнута.

Пример 23. В следующей таблице представлены данные о чис­ле сделок, заключенных на фондовой бирже за квартал, для 517 инвесторов.

i	0	1	2	3	4	5	6	7
	112	168	130	68	32	5	1	1

В первой строке приведены числа сделок, во второй – числа инвесторов, заключивших столько сделок за квартал.

Требуется проверить, используя критерий Пирсона, что на уровне значимости число сделок, заключенных одним инвестором за квартал, распределено по закону Пуассона с па­раметром .

Решение. Поскольку распределение Пуассона дискретно, в качестве различных исходов здесь можно взять сами значения случайной величины. Заметим, что последние два значения (6 и 7) встретились слишком мало раз, поэтому их следует объеди­нить с предыдущим (5). Кроме того, распределение Пуассона не ограничено справа, и следует учесть все значения, большие 7 (которые не встретились ни разу).

Находим теоретические вероятности по формуле распреде­ления Пуассона

.

При получаем:; ; ; ; . Умножим их на число инвесторов п = 517 и составим следу­ющую таблицу:

i
0	112	115,34	– 3,34	0,10
1	168	173,04	– 5,04	0,15
2	130	129,77	0,23	0,00
3	68	64,88	3,12	0,15
4	32	24,35	7,65	2,40
5	7	9,62	– 2,62	0,71

Суммируя значения в последнем столбце, получаем значе­ние статистики хи-квадрат = 3,51.

По таблице критических точек распределения хи-квадрат по уровню значимости и числу степеней свободы6 – 1 = 5 находим критическую точку  = 11,1. Поскольку , мож­но считать, что число сделок, заключенных одним инвестором за квартал, распределено по закону Пуассона с параметром = 1,5.

Замечание. Если бы значение параметра  = 1,5 было оценено по самой выборке, следовало задать число степеней сво­боды 6 – 2 = 4. Тогда  = 9,5, так что гипотеза тоже принимается.

Пример 24. В виде статистического ряда приведены сгруппированные данные о времени безотказной работы 400 приборов:

Время безотказной работы (в часах)	от 0 до 500	от 500 до 1000	от 1000 до 1500	от 1500 до 2000
Число приборов	257	78	49	16

Согласуются ли эти данные с предположением, что время безотказной работы прибора имеет функцию распределения ? Уровень значимости взять, напри­мер, равным 0,025.

Вычислим вероятности, приходящиеся в соответствии с гипотезой на интервалы. Например,

= Р(0 < X < 500) = F(500) – F(0) = 1 – е^–1 – 1 + = = 0,6324;

Составим таблицу

257	0,6324	252,96	4,04	0,06
78	0,2325	93	– 15	2,42
49	0,0852	34,08	14,92	6,53
16	0,0317	12,68	3,32	0,97

Суммируя значения в последнем столбце, получаем значе­ние статистики хи-квадрат = 9,88.

По таблице 2 критических точек распределения хи-квадрат по уровню значимости и числу степеней свободы 4– 1 = 3 находим критическую точку = 9,4. Значение = 9,88входит в критическую область.

Вывод: гипотеза противоречит опыт­ным данным. Гипотезу отвергаем и вероятность того, что это делается ошибочно, равна 0,025.

Пример 25. Дня интервального статистического ряда проверить гипотезу о нормальности распределения с помощью Критерия Пирсона.

Границы интервалов	5 – 7	7 – 9	9 – 11	11 – 13	13 – 15	15 – 17
	8	14	40	26	6	4

Решение. Объем выборки Для каждого интервала найдем середины

Границы интервалов	5 – 7	7 – 9	9 – 11	11 – 13	13 – 15	15 – 17
Середины интервалов	6	8	10	12	14	16
	8	14	40	26	6	4

Для проверки гипотезы о нормальном распределении выборки найдем оценки математическою ожидания и дисперсии:

Выдвигаем основную гипотезу:

: генеральная совокупность подчиняется нормальному закону рас­пределения. Тогда альтернативная гипотеза принимает вид: : закон распределения не является нормальным. Задаемся уровнем значимости

Расширяя границы первого и последнего интервалов, результаты всех вычислений сведем в таблицу.

Границы интервала	Частота
– ∞ – 7	8	0,0681	6,6738	0,2635
7 – 9	14	0,1995	19,551	1,5761
9 – 11	40	0,3350	32,830	1,5659
11 – 13	26	0,2682	26,2836	0,0306
13 – 15		0,1064		0,5595
15 – +∞		0,0228
	98	1,0000		3,995

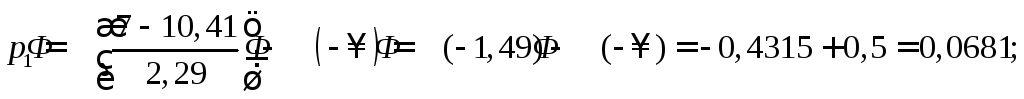
Частота шестого интервала меньше 5, поэтому объединяем его с пятым интервалом во втором и четвертом столбце.

Пятый столбец таблицы является результатом вычислений по формуле: .Не следует забывать, что пятый и шестой интервалы объединены.

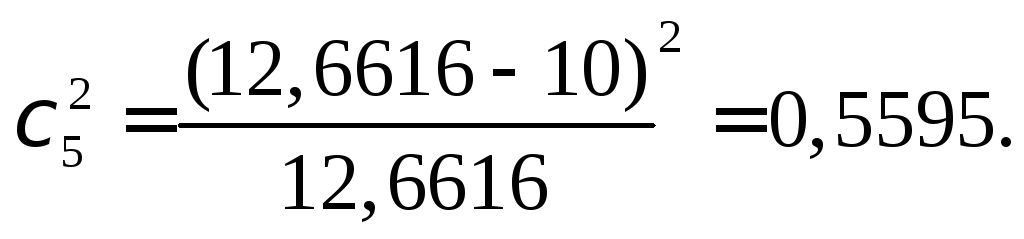
Таким образом,

Так как после объединения осталось 5 интервалов (), а по выборке определены оценки двух параметров, т.е. то число степеней свободы рав­но 5 –2 – 1 = 2, по таблице 2 критических точек распределения хи-квадрат найдем

Сравнивая полученные значения, видим, что следовательно, гипотеза о нормальном распределении не отвергается.

Пример 26. Для эмпирического распределения рабочих цеха по выработке по данным таблицы подобрать соответствующее теоретическое распределение и на уровне значимости проверить гипотезу о согласованности двух распределений с помощью критерия хи-квадрат.

i	Выработка в отчетном году в процентах к предыдущему х	Частота (количество рабочих)	Относительная частота
1	94 – 100	3	0,03
2	100 – 106	7	0,07
3	106 – 112	11	0,11
4	112 – 118	20	0,20
5	118 – 124	28	0,28
6	124 – 130	19	0,19
7	130 – 136	10	0,10
8	136 – 142	2	0,02
	Σ	100	1,00

Решение. По виду гистограммы распределения рабочих по выработке можно предположить нормальный закон распределения признака.

Параметры нормального закона распределения а и , являющиеся соответственно математическим ожиданием и дисперсией случайной величины Х, неизвестны, поэтому заменяем их «наилучшими» оценками по выборке  –несмещенными и состоятельными оценками соответственно выборочной средней и «исправленной» выборочной дисперсией . Так как число наблюдений n = 100 достаточно велико, то вместо «исправленной» можно взять «обычную» выборочную дисперсию. Имеем,,.

Итак, выдвигается гипотеза :.

Для расчета вероятностей попадания случайной величины Х в интервал используем функцию Лапласа в соответствии со свойством нормального распределения:

.

Например,

.

и соответствующая первому интервалу теоретическая частота и т.д.

Для определения статистики удобно составить таблицу:

i	Интервал	Эмпири-ческие частоты	Вероят-ности	Теорети-ческие частоты
1	94 – 100		0,017		5,76	0,758
2	100 – 106		0,059
3	106 – 112	11	0,141	14,1	9,61	0,682
4	112 – 118	20	0,228	22,8	7,84	0,344
5	118 – 124	28	0,247	24,7	10,89	0,441
6	124 – 130	19	0,182	18,2	0,64	0,035
7	130 – 136		0,087		0,16	0,014
8	136 – 142		0,029
	Σ	100	0,990	99,0	–

Учитывая, что в рассматриваемом эмпирическом распределении частоты первого и последнего интервалов (, ) меньше 5, при использовании критерия – Пирсона целесообразно объединить указанные интервалы с соседними (см. таблицу). Итак, фактически наблюдаемое значение статистики .

Так как новое число интервалов (с учетом объединения крайних) , а нормальный закон распределения определяется параметрами, то число степеней свободы . Соответствующее критическое значение статистики по таблице 2 приложения . Так как , то гипотеза о выбранном теоретическом нормальном законе с параметрамиN(119,2; 87,48) согласуется с опытными данными.

Пример 27. Имеются сгруппированные данные о дневной вы­ручке в магазине электротоваров (в тыс. руб.):

Суммы продаж	Число продаж
190 – 200	10
200 – 210	26
210 – 220	56
220 – 230	64
230 – 240	30
240 – 250	14

Пользуясь критерием согласия Колмогорова, проверить гипотезу о том, согласуются ли данные о распределении дневной выручки в магазине электротоваров с предположением о их распределении по нормальному закону. Уровень значимости принять.

Решение. Для проверки этой гипотезы определим значения –середин интервалов и найдем точечные оценки математического ожида­ния и среднего квадратического отклонения нормально распределенной случайной величины X.

; .

При достаточно большом объеме выборки можно принять то­чечные оценки параметров предполагаемого нормального закона за ис­тинные значения а и σ.

Итак, . Эту гипотезу будем проверять.

Для проверки нулевой гипотезы используем критерий согласия Колмогорова

.

Для нахождения составим расчетную таблицу.

Интервалы	Частоты	Накопленные частоты	Нормированные интервалы
Менее 190	0	–	()
190 – 200	10	10	()
200 – 210	26	36	()
210 – 220	58	92	()
220 – 230	64	156	()
230 – 240	30	186	()
240 – 250	14	200	()
	200	–	–

Интервалы	Значения эмпирической функции для правого конца интервала	Теоретическая функция распределения
Менее 190	0,00	0,006	0,006
190 – 200	0,05	0,045	0,005
200 – 210	0,18	0,186	0,007
210 – 220	0,46	0,468	0,008
220 – 230	0,78	0,767	0,013
230 – 240	0,93	0,938	0,008
240 – 250	1,00	1,0000	0,000

λ_набл = .

По таблице 5 критических точек распределения Колмогорова при находим .

Так как λ_набл < λ_крит , то нет оснований для отклонения нулевой гипо­тезы о нормальном законе распределения.

Поэтому расхождение между теоретическим и эмпирическим распределениями может быть случайным и, следовательно, модель зако­на нормального распределения приемлема с большей степенью уверен­ности.

Пример 28. Из данных, характеризующих процент верных от­ветов, поученных студентами при тестировании, извлечены две выборки с объемами и . Первая выборка осуществлена до начала учебных занятий, а вторая – после 6–часовых занятий.

Процент верных ответов	Частота в выборке № 1	Частота в выборке № 2
96 – 100	15	18
91 – 95	10	8
86 – 90	4	2
81 – 85	3	5
76 – 80	2	6
71 – 75	1	2
66 – 70	1	2
61 – 65	1	4
56 – 60	–	1
51 – 55	1	1
46 – 50	1	–
41 – 45	1	1

Требуется с помощью критерия Колмогорова-Смирнова про­верить, что распределение правильных ответов в % описывается одной и той же функцией рас­пределения. Уровень значимости принять равным 0,01.

Решение. – (две выборки из одной и той же гене­ральной совокупности). Проверка нулевой гипотезы основывается на вычислении ста­тистики критерия Колмогорова-Смирнова.

где , a и выборочные эмпирические функции.

Накопленные частоты
40	50	1,00	1,00	0,00
25	32	0,63	0,64	0,01
15	24	0,38	0,48	0,10
11 8	22 17	0.28	0,44	0,16
8	17	0,2	0,34	0,14
6	11	0,15	0,22	0,07
5	9	0,13	0,18	0,05
4	7	0,10	0,14	0,04
3	3	0,08	0,06	0,02
3	2	0,08	0,04	0,04
2	1	0,05	0,02	0,03
1	1	0,03	0,02	0,01

Просматривая последний столбец таблицы, видим, что наи­больший модуль разности между эмпирическими функциями распределе­ния и равен .

Так как то наблюдаемое значение выборочное статистики . Найдем по таблице критических точек   распределения Колмогорова и заданному уровню значимости . Так как = 0,75 < 1,62, то нет оснований для отклонения нулевой гипотезы.

Пример 29. В течение месяца выборочно осуществлялась проверка торговых точек города по продаже овощей. Результаты двух проверок по недовесам покупателям одного вида овощей приведены в таблице.

Номер интервала	Интервалы недовесов, г	Частоты
		, для выборки 1	, для выборки 2
1	0 – 10	3	5
2	10 – 20	10	12
3	20 – 30	15	8
4	30 – 40	20	25
5	40 – 50	12	10
6	50 – 60	5	8
7	60 – 70	25	20
8	70 – 80	15	7
9	80 – 90	5	5

Можно ли считать, что на уровне значимости по результатам двух проверок (случайных выборок) недовесы овощей описываются одной и той же функцией распределения?

Решение. Обозначим: и– накопленные частоты соответственно выборок 1 и 2;,– значения их эмпирических функций распределения. Результаты вычислений сведем в таблицу.

xi
10	3	5	0,027	0,050	0,023
20	13	17	0,118	0,170	0,052
30	28	25	0,254	0,250	0,004
40	48	50	0,436	0,500	0,064
50	60	60	0,545	0,600	0,055
60	65	68	0,591	0,680	0,089
70	90	88	0,818	0,880	0,072
80	105	95	0,955	0,950	0,005
90	110	100	1,000	1,000	0,000

Из последнего столбца видно, что

.

По формуле

наблюдаемое значение статистики критерия Колмогорова-Смирнова при , равно:

.

По таблице 5 критических точек   распределения Колмогорова и заданному уровню значимости найдем Так как (0,644 < 1,36), то нулевая гипотезане отвергается, следовательно, недовесы покупателям описываются одной и той же функцией распределения, т.е. они являются устойчивым и закономерным процессом при продаже овощей в данном городе.

Пример 30. Две группы выпускников двух высших заведений (1 и 2) по 10 человек в каждой получили оценки своих административных способностей (в баллах), приведенные ниже в таблице.

	26	22	19	21	14	18	29	17	11	34
	16	10	8	13	19	11	7	13	9	21

Можно ли утверждать на уровне значимости , что не существует различия в уровне подготовки выпускников вузов?

Решение. Составим упорядоченную объединенную выборку объема и определим ранги оценок выпускников.

Оценка	7	8	9	10	11	11	13	13	14	16
Номер вуза	2	2	2	2	1	2	2	2	1	2
Ранг	1	2	3	4	5,5	5,5	7,5	7,5	9	10
Оценка	17	18	19	19	21	21	22	26	29	34
Номер вуза	1	1	1	2	2	1	1	1	1	1
Ранг	11	12	13,5	13,5	15,5	15,5	17	18	19	20

Находим суммы рангов оценок для первой и второй выборок:

Проверяем выполнение равенства (5.2):

действительно,

Находим значение статистик U и t по формулам (5.1) и (5.3):

По таблице 1 приложения при . Так как , то нулевая гипотеза отвергается, т.е. уровни подготовки выпускников двух вузов существенно отличаются (в первом вузе он существенно выше, так как ). Полученный вывод интуитивно ясен, так как в объединенной выборке низкие ранги (низкие оценки) получили преимущественно выпускники второго вуза, а высокие ранги (высокие оценки) – первого вуза.

Пример 31. Температура в холодильной камере контроли-руется по двум электронным термометрам. Для сравнения точности термометров их показания фиксируются одновременно. Проведено 10 замеров показаний термометров:

Номер заказа	Термометр 1	Термометр 2
1	– 7,11	– 7,13
2	– 8,63	– 8,49
3	– 6,89	– 7,12
4	– 7,23	– 7,19
5	– 7,51	– 7,67
6	– 7,68	– 7,49
7	– 7,91	– 8,03
8	– 6,97	– 7,15
9	– 7,44	– 7,29
10	– 7,64	– 7,89

При уровне значимости 0,1 проверить гипотезу о равенстве дисперсий.

Решение. Для решения поставленной задачи, необходимо проверить гипотезу при альтернативной . Воспользуемся инструментом Пакета анализа MS Excel Двухвыборочный F-тест для дисперсии.

1. Сформируем таблицу исходных данных в MS Excel:

2. Перейдем на вкладку Данные – Анализ данных и в раскрывающемся списке выберем Двухвыборочный F-тест для дисперсии.

3. В появившемся окне вводим следующие данные:

4. Результат вычислений представлен следующим образом:

Где df – число степеней свободы, а F – F_набл. (наблюдаемое).

Так F < f_кр, то делаем вывод о том, что нет оснований отвергнуть гипотезу H₀.

Пример 32. Имеются две независимые выборки из генеральных совокупностей X и Y, генеральные дисперсии известны:

X	Y
2,53	2,65
2,92	2,66
2,87	1,82
3,22	3,89
3,55	4,62
4,91	6
4,56	5,91
3,75	2,53
1,45	1,84
3,28	2,29

При уровне значимости проверить гипотезу H₀:  при конкурирующей гипотезе H₁: 

Решение. Эту задачу можно решить, воспользовавшись инструментом Пакета анализа MS Excel Двухвыборочный Z-тест для средних. Для этого необходимо:

1. Сформировать таблицу исходных данных:

2. Перейти на вкладку Данные – Анализ данных. В появившемся окне выбрать Двухвыборочный Z-тест для средних.

3. В окне теста ввести исходные данные:

4. В результате выполнения теста будут получены следующие результаты:

5. На основании полученных данных можно сделать вывод о том, что оснований отвергнуть гипотезу H₀ нет, т.к. z < z_кр.

Пример 33. Используя критерий Пирсона, при уровне значимости  a = 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.

5	5	5	5	5	5	5	5	5	5
5	5	5	5	5	7	7	7	7	7
7	7	7	7	7	7	7	7	7	7
7	7	7	7	7	7	7	7	7	7
7	9	9	9	9	9	9	9	9	9
9	9	9	9	9	9	9	9	9	9
9	9	9	9	9	9	11	11	11	11
11	11	11	11	11	11	11	11	11	11
11	11	11	11	11	11	11	11	11	11
11	11	11	11	11	11	13	13	13	13
13	13	13	13	13	13	13	13	13	13
13	13	13	13	13	13	13	13	13	13
13	13	15	15	15	15	15	15	15	15
15	15	15	15	15	15	15	15	15	15
15	15	15	17	17	17	17	17	17	17
17	17	17	17	17	17	17	17	17	17
17	17	17	17	17	17	17	19	19	19
19	19	19	19	19	19	19	19	19	19
19	19	19	19	19	19	19	21	21	21
21	21	21	21	21	21	21	21	21	21

Решение. Воспользуемся средствами MS Excel для решения задачи. Для этого:

1. Сформируем таблицу исходных данных:

2. Вычислим выборочное среднее. Для этого выберем ячейку A22 и перейдем на вкладку Формулы – Другие функции – Статистические и в раскрывающемся списке выберем функцию СРЗНАЧ. В появившемся окне в поле Число 1 введем диапазон исходных данных (A1:J20). После нажатия кнопки ОК в ячейке А22 появится результат вычисления (12,63)

3. Теперь вычислим выборочное среднее квадратическое отклонение. Для этого выберем ячейку A23 и перейдем на вкладку Формулы – Другие функции – Статистические и в раскрывающемся списке выберем функцию СТАНДОТКЛОН.В. В появившемся окне в поле Число 1 введем диапазон исходных данных (A1:J20). После нажатия кнопки ОК в ячейке А23 появится результат вычисления (≈4,71)

4. Вычислим теоретические частоты по формуле (учитывая, что n = 200, h = 2):

Для этих вычислений составим расчётную таблицу:

Значения в столбце u_i вычисляются по формуле: . Для этого в ячейку C26 введем формулу: =(B26–$A$22)/$A$23. По нажатия кнопки Enter в ячейке C26 отобразится результат вычисления. Теперь перенесём эту формулу вниз по столбцу до последнего значения (21). Для этого выберем ячейку C26 и, зажав в нижнем левом углу ячейки квадрат, растянем её до последнего значения.

Для подсчёта значений в столбце Ф(ui) воспользуемся статистической функцией ФИ. Для этого выберем ячейку D26 и перейдем на вкладку Формулы – Другие функции – Статистические и в раскрывающемся списке выберем функцию ФИ. В появившемся окне в поле x введем значение ui (С26). После нажатия кнопки ОК в ячейке D26 появится результат вычисления. Перенесем эту формулу для остальных значений, как в предыдущем случае.

И, наконец, для подсчёте значений последнего столбца ni' выберем ячейку E26 и введем в неё формулу: =200*2/$A$23*D26 и перенесём формулу, как в предыдущих случаях.

5. Сравним эмпирические и теоретические частоты. Для этого снова составим расчётную таблицу:

Для подсчёта значения эмпирической частоты в столбце n_i воспользуемся статистической функцией СЧЁТЕСЛИ. Для этого выберем ячейку С37 и перейдем на вкладку Формулы – Другие функции – Статистические и в раскрывающемся списке выберем функцию СЧЁТЕСЛИ. В появившемся окне в поле диапазон введем диапазон исходных данных (A1:J20), а в поле критерий – B37. После нажатия кнопки ОК в ячейке C37 появится результат вычисления. Перенесем эту формулу для остальных значений.

Значения теоретической частоты скопируем из предыдущей расчётной таблицы.

Для подсчёта разности в столбце n_i – n_i' в ячейку E37 введём формулу: = C37–D37. После нажатия кнопки Enter в ячейке E37 появится результат вычисления. После этого перенесём эту формулу для всех оставшихся значений.

Чтобы посчитать квадрат разностей выберем ячейку F37 и перейдем на вкладку Формулы – Математические. Из раскрывающегося списка выберем функцию СТЕПЕНЬ. В появившемся окне в поле число введём E37, а в поле степень введём число 2. После нажатия кнопки ОК в ячейке F37 появится результат вычисления. Перенесем эту формулу для остальных значений.

Для подсчёта значений в последнем столбце введём следующую формулу в ячейку G37: = F37/D37. После нажатия кнопки Enter в ячейке G37 появится результат вычисления. Перенесём эту формулу для остальных значений.

Теперь выделим все ячейки с значениями в последнем столбце и перейдем на вкладку Формулы. Выберем функцию Автосумма. В ячейке G46 появится результат сложения всех значений (22,14) – это и есть .

6. Найдем значение по таблице критических точек распределения с уровнем значимости α = 0,05 и числу степеней свободы находим критическую точку правосторонней критической области .

7. , т.е. наблюдаемое значение попадает в критическую область. Значит, гипотезу о нормальном распределении генеральной совокупности отвергаем.