Вопросы для самоконтроля

1.Что характеризует точность оценки параметра?

2. Что называется надежностью (доверительной вероят-ностью) оценки? Как она обозначается?

3. Что называется доверительным интервалом для оцениваемого параметра с заданной надежностью?

4. Какой вид имеют доверительные границы довери-тельного ин­тервала?

5. Что называется предельной погрешностью точечной оценки параметра?

6. Что происходит с длиной доверительного интервала при увеличении объема выборки? увеличении доверительной вероятности?

7. Являются ли концы интервалов постоянными величи-нами? Случайными величинами?

8. Опишите общую схему построения доверительного интервала.

9. Укажите формулу для доверительного интервала а параметра нормального распределения.

10. Укажите формулу для доверительного интервала параметра нормального распределения.

11. Как строится доверительный интервал для неизвестной вероятности события?

12. Чем отличается вероятностный подход к определению точности оценки от принятого в математическом анализе?

13. Объясните, почему доверительный интервал для мате-матиче­ского ожидания при известной дисперсии находится точно, если наблюдаемая случайная величина распределена нормально, а в произ­вольном случае – приблизительно и лишь при больших выборках.

Образцы решения типовых задач

Пример 1. Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределенной генеральной совокупности (по выбо­рочному среднему ) равна , если известно среднее квадратическое отклонение генеральной совокупности.

Решение. Формула, определяющая точность оценки математического ожидания генеральной совокупности по выборочной средней, имеет вид Отсюда следует, что (при этом п обычно округляется в большую сторону для надежности). По таблице функции Лапласа находим для данного примера, учитывая, что функция принимает значение  = 0,925/2 = 0,4625. Таким образом, . Подставляя данные этой задачи, получаем искомый объем выборки п:

Берем округленно п = 179.

Пример 2. Произведено 5 независимых наблюдений над с.в. ~ Результаты наблюдений таковы: , , , . Найти оценку для , а также построить для него 95%-й доверительный интервал.

Решение. Находим сначала (–25 + 34 ­– 20 + 10 + + 21)/5 = 4. Учитывая, что и, получаем . По таблице (функции Лапласа) выясняем, что Тогда Доверительный интервал для a = M(X)  таков: (4 – 17,5; 4 + 17,5), т.е. (–13,5; 21.5).

Пример 3. По условию примера 2, считая, что с.в. ~ , построить для неизвестного M(X) = а доверительный интервал. Считать = 0,95.

Решение. Оценку для M(X) уже знаем: . Находим значение s: ((–25 – 4)² + (34 – 4)² + (–20 – 4)² + + (10 – 4)² + (21 – 4)²)/4 = 660,5; s 25,7.

По таблице 3 для = 0,95 и находим . Следовательно, Доверительный интервал таков: (–27,9; 35,9).

Пример 4. Произведено 20 опытов над случайной величиной X, распределенной по нормальному закону. Требуется построить доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности если получены оценки математического ожидания и дисперсии:

Решение. По таблице 3 для числа степеней свободы и доверительной вероятности находим значение Тогда

Доверительный интервал для математического ожидания принимает вид

Если доверительная вероятность то уровень значимости

По таблице 2 приложения найдем значения критических точек распределения

Доверительный интервал для дисперсии:

.

.

Пример 5. В таблице приведены сгруппированные данные измерений роста у 50 случайно отобранных студентов.

Рост студентов, см	162–166	166–170	170–174	174–178	178–182	182–186
Число студентов	3	7	15	13	11	1

Построить доверительный интервал для среднего роста студентов с надёжностью 0,9.

Решение. Так как данные сгруппированы, то в качестве представителя каждой группы можно взять середину интервала. Тогда

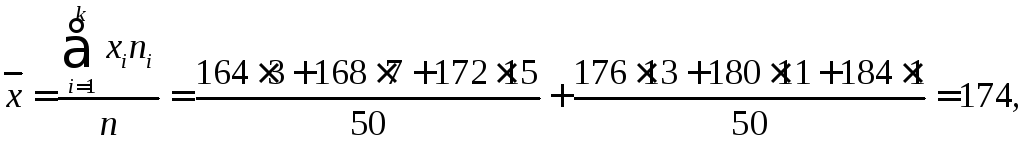
s = 4,87.

По таблице функции находим значение для которого Тогда по формуле

находим

или

Пример 6. Измерения сопротивления резистора дали следующие результаты (в омах):

Известно, что ошибки измерения имеют нормальный закон распределения. Систематическая ошибка отсутствует. Построить доверительный интервал для истинного сопротивления резистора с надёжностью 0,99 в предположении:

а) дисперсия ошибки измерения известна и равна 4;

б) в предположении неизвестной ошибки измерения.

Решение. Результаты измерения можно представить в видеX = a + Y, где a – истинное значение измеряемой величины, а Y – ошибка измерения. Систематическая ошибка отсутствует (), поэтому и ,т.е. доверительный интервал для M(X) будет доверительным интервалом для истинного значения сопротивления резистора. В данной серии наблюдений

Если дисперсия известна, то доверительный интервал можно построить, используя устойчивость нормального закона распределения. Так как и, то, откуда

Из таблицы функции Лапласа находим, что

Тогда или

В результате

или

.

В случае неизвестной дисперсии, её оценку можно получить на основе тех же опытных данных

.

По таблице 3 критических точек распределения Стьюдента для степеней свободы и заданной вероятностинаходим такое, что

,

.

Пример 7. С целью определения средней суммы вкладов в сберегательной кассе, имеющей 7200 вкладчиков, произведено выбороч­ное обследование (бесповторный отбор) 111 вкладчиков, которое дало следующие результаты:

Сумма вклада, тыс. руб.	10 – 30	30 – 50	50 – 70	70 – 90	90 –110	110 –130
Число вкладов	1	3	10	30	60	7

Пользуясь этими данными, найдите доверительные границы для генерального среднего, которые можно было бы гарантировать с вероят­ностью 0,95.

Решение. – неизвестно, но при больших n . Сначала найдем выборочную среднюю и выборочную дисперсию при помощи расчетной таблицы:

Интервалы
10 – 30	20	1	20	400
30 – 50	40	3	120	4800
50 – 70	60	10	600	36 000
70 – 90	80	30	2400	192 000
90 – 110	100	60	6 000	600 000
110 – 130	120	7	840	100 800
–	–	111	9980	934 000

Так как и (cм. таблицу 1 приложения), то предельная погрешность = 1,961,68 = 3,3826 и до­верительными границами для генерального среднего будут и

Пример 8. Аналитик фондового рынка оценивает среднюю доходность определенных акций. Случайная выборка 15 дней показала, что средняя (годовая) доходность с исправленным сред­ним квадратическим отклонением s = 3,5%. Предполагая, что доход­ность акций подчиняется нормальному закону распределения, построй­те 95%-ный доверительный интервал для средней доходности интере­сующего аналитика вида акций.

Решение. – неизвестно, и поскольку объем выборки  п = 15, то необ­ходимо применить распределение Стьюдента с степенями свободы. В таблице 3 приложения на пересечении строки, соответст­вующей 14 степеням свободы, и колонки, соответствующей уровню зна­чимости а = 0,05 для двусторонней критической области, находим . Используя это значение, построим 95%-ный доверитель­ный интервал:

(8,44; 12,3).

Следовательно, аналитик может быть на 95% уверен, что сред­няя годовая доходность по акциям находится между 8,44% и 12,3%.

Пример 9. Определите численность выборки при обследова­нии остатков на расчетных счетах у клиентов коммерческого банка, что­бы с вероятностью 0,683 ошибка репрезентативности не превышала 5 тыс. руб., если σ_ген = 120 тыс. руб.

Решение. – известно. Предполагается, что выборка – повторная. По таблице 1 приложения по заданной доверительной вероятности находим аргумент функции Лапласа

Следовательно, объем выборки, при котором с вероятностью 0,683 можно утверждать, что средняя выборочная отлича­ется от генеральной по абсолютной величине меньше чем на 5 тыс. руб., определяется по формуле

Пример 10. По случайной выборке измерений роста 20 студен­тов первого курса Смоленского университета вычислена несмещенная оценка генеральной дисперсии Найдите 95%-ный довери­тельный интервал для среднего квадратического отклонения роста всех студентов первого курса Смоленского университета, если распределе­ние роста нормально.

Решение. = 0,95, 1–α = 0,95, α = 0,05. Для нахождения искомого доверительного интервала по таблице 2 приложения найдем

и

Искомый доверительный интервал имеет вид:

Пример 11. Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что исправленное среднее квадратическое отклонение для числа рабо­тающих на фирме составляет s = 25 (человек). Пользуясь 90%-ным доверительным интервалом, оценить среднее квадратическое от­клонение для числа работающих на фирме по всей отрасли, пост­роив доверительный интервал.

Решение. Доверительный интервал для параметра имеетвид

где и находят по таблице критических точек распределения хи-квадрат. По таблице 2 приложения определяем для данного примера

Подставляя в формулу необходимые ве­личины, получаем искомый доверительный интервал:

19,74 < < 34,61 (человек).

Пример 12. На основании выборочных наблюдений производительности труда 20 работниц было установлено, что среднее квадратическое отклонение суточной выработки составляет 15 м ткани в час. Предполагая, что произво-дительность труда работницы имеет нормальное распределение, найти границы, в которых с надёжностью 0,9 заключены генеральные дисперсия и среднее квадратическое отклонение суточной выработки работниц.

Решение. Имеем

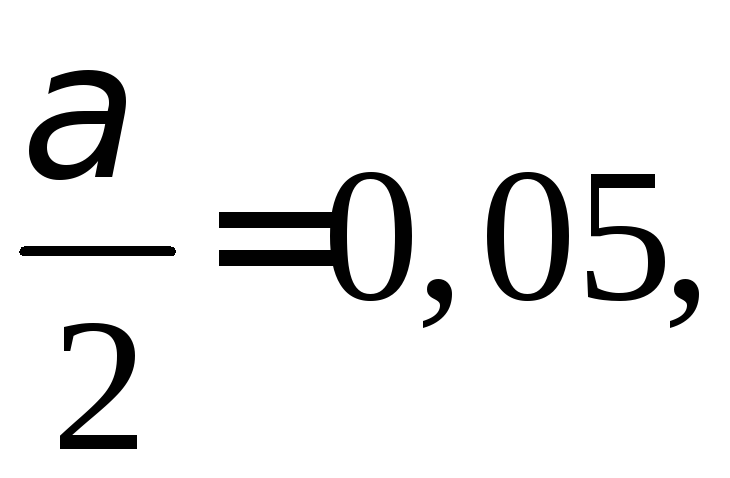
При числе степени свободы по таблице 2 приложения определим = 30,1 и = 10,1. Тогда доверительный интервал для можно записать в виде:

или

и для :

или (м/ч).

Итак, с надёжностью 0,9 дисперсия суточной выработки работниц заключена в границах от 142 до 423,3, а её среднее квадратическое отклонение – от 12 до 20,7 метров ткани в час.

Пример 13. Для определения процента вкладов, не превы­шающих 100000 руб., произведена повторная выборка 900 лицевых сче­тов. Среди них оказалось 30% вкладов не более 100000 каждый. С какой доверительней вероятностью можно утверждать, что процент таких вкладов в данной кассе будет отличаться от найденного не более чем на 2%?

Решение. n = 900; ;. Так как , то

.

Искомая вероятность Р = = 2 = 2 0,4049 = 0,8098.

Пример 14. Для обследования крупной парии изделий отобрано наугад 900 штук. Проверка показала, что среди них 810 стандартны. Построить доверительный интервал для доли стандартных изделий в партии. Уровень надёжности выбрать равным 0,95.

Решение. Пусть доля стандартных изделий в партии равна p. Оценкой её может служить величина По таблице функции Лапласа находим такое чтобыТогда по формуле

.

Пример 15. Из партии, содержащей 10000 музыкальных цен­тров «Samsong», отобрано 3000 штук. В выборке оказалось 4% музыкаль­ных центров с бракованными компакт-дисками. Определите границы, в которых заключена доля стандартных музыкальных центров в генераль­ной совокупности, если результат необходимо гарантировать с вероятно­стью, равной 0,9976.

Решение. Имеем N = 10000; n = 3000; По заданной вероятности 0,9976 найдем = 0,4938 и по таблице 1 приложения определим = (0,4938) = 2,5. Получим предельную ошибку выборки:

= 2,5·0,0036 = 0,009 (≈ 0,9%).

Тогда доверительными границами для генеральной доли будут

= 0,04 – 0,009 = 0,031 (≈ 3,1%)

и

= 0,04 + 0,009 = 0,049 (≈ 4,9%).

Пример 16. Сколько лиц в возрасте от 20 до 30 лет надо опро­сить выборочно, чтобы установить среди них процент студентов с точно­стью до 0,5%, гарантируемой с вероятностью 0,9999?

Решение. ; = 0,9999; п = ?

По заданной доверительной вероятности находим

.

Следовательно, объем выборки, при котором с вероятностью 0,9999 можно утверждать, что выборочная доля отличается от генеральной доли по абсолютной величине меньше чем на 0,5%, определяется по формуле

.

При определении средней квадратической ошибки выборки для доли, если даже выборочная доля неизвестна, в качестве можно взять его максимально возможное значение

()_max = [p*(1–p)*]_max = 0,5·0,5 = 0,25 .

Тогда n_max = 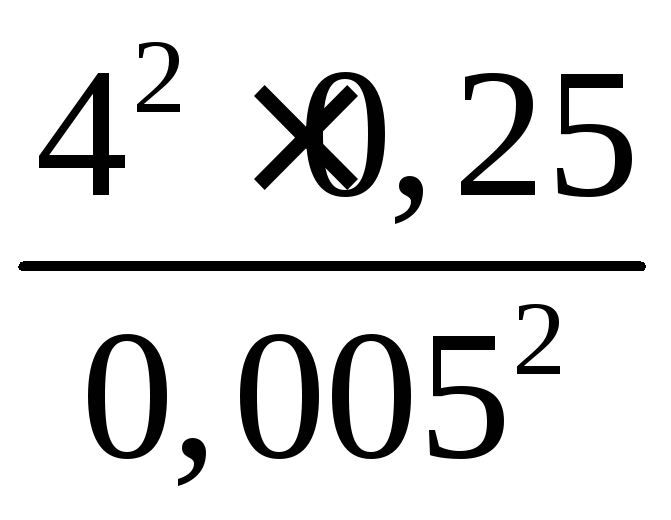= 160000.

Пример 17. За последние 5 лет годовой рост цены актива А со­ставлял в среднем 20% со средним квадратическим отклонением (исправленным) 5%. Построить доверительный интервал с ве­роятностью 95% для цены актива в конце следующего года, если и начале года она равна 100 ден. ед.

Решение. Рассмотрим величины относительного прироста пены актива за год. Будем пользоваться нормальным приближе­нием. Применяем формулу

где находим из таблицы 3 критических точек распределения Стьюдента: Получаем,

0,2 – 0,05∙2,78 < x₆ < 0,2 + 0,05∙2,78,

откуда

0,05 < < 0,35.

Таким образом, цена актива в следующем году составит от 105 до 135 ден. ед.

Пример 18. Случайная величина Х имеет нормальное распре-де­ление с известным средним квадратическим отклонением Найти доверительный интервал для неизвестного математичес­кого ожидания а по выборочному среднему , если объем вы­боркип = 36 и задана надежность оценки = 0,95.

Решение. Для решения этой задачи воспользуемся статистической функцией в MS Excel ДОВЕРИТ.НОРМ, для этого:

1. На листе MS Excel выбрать ячейку, в которую будет помещен результат вычисления значения доверительного интервала.

2. Перейти на вкладку Формулы-Другие функции-Статистические и в раскрывающемся списке выбрать ДОВЕРИТ.НОРМ

3. Ввести исходные данные в поля:

где Альфа=1-β

4. Доверительный интервал для математического ожидания a по выборочному среднему 5 (): (4,02; 5,98).