Основные структуры классической математики

x~y Û x y ) ($iÎ I x, yÎ Ai).

+, a~b, a, bÎ A4, a~c. , ! ~ %, , . .

1 ) A.

, ! 1 r

) A. $ S ) A, 2

) [a]ρ = {xÎ A: xra}, aÎ A. 0 ),

[a]ρ

S = A/r = {[a]ρ: aÎ A}Í B(A)

) A. % ! r aÎ [a]ρ

aÎ A. 4, 1) 3),

2 . 0 2)

* [a]ρ [b]ρ S ), [a]ρ = [b]ρ. $), cÎ [a]ρÇ[b]ρ. 0 xÎ [a]ρ cra, crb xra, (arc) !

r xrc xrb. (, [a]ρÍ [b]ρ. $1

[b]ρÍ [a]ρ. 4 , [a]ρ = [b]ρ.

. * (Ai)i I ® ~ ρ ® A/ρ 4 #

% A *

2 A.

( ! . 0 1 ~ A 1 aÎ A ~ = [a]~. + a, bÎ A

~ = ~ Û a~b. b

$1 ) (Ai)i I ® ~ r ® A/r .

0 ! 1 r ) A

A/r '- ) A 1 r. $ * .

*. 1. ! =

) A, 1 A/= º A.

2.! n, nÎ N, ) Z

: a º b(mod n) , a–b n .

_____

-) Z/ºn = Zn = { 0,1,..., -1} – 1 )

n, * n.

41

3.! )

. , %-)

) .

4.! ) . 4 * %-) )

«%» .

5." ! %

O ) .

-) !

) ) )

O, ) ) {O}. 9 %-) ) ) )

( )).

6. ! 4 ~ ) !

) U. -) U/~ )

) * () ). 0

) 440, ) *

.

7. ! ~f ) A

) f: A ® B: x~fy Û f(x)=f(y) x, yÎ A. -

) A/~f = {f-1(b): bÎ Im f} ) ) Im f.

$ . 11. , ) A !

£, ! <,

! £ ¹, ) A. ,

< – ) A,

! £, 2 ! < =,

! ) A. + )

) A

. 0 ) 1 ).

12. !

! ).

13. $ r – ! ) A. 0

1 a, bÎ A ) a~b, arb bra. $), ! ~ 1 A. . %-) A/~ ! £ %

40 * ) % , )

* ). 4. % 3.4.

42

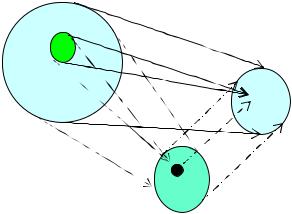
$ 1 ).

14. $), !

(A~B Û A = B ) ) )

) 1. :

* %-)?

15. . ) R

! r %: arb , a–bÎ Z (a, bÎ R). 0 ),

r – 1 R. 0

%-) R/r.

16. ' * : 0

2 f: A ® B * g: A/~→ B,

, f=pg, p: A→ A/~ – ) %-

) ) A ! : a~b af=bf.

) ) X. 0 A, BÎ S

): ArB Û AÇB¹Æ. $), ! r

! S. (, !

r [24].

18. $ . 36,

, , 2 2

! %.

43

1.3. ( !

$ S – ) ). 0 )

A B M(A, B)41 ) ) A → B. # !, ) A, B C *

)

M(A, B)×M(B, C) → M(A, C),

* ) (f, g) )

f: A → B g: B → C fg: A → C. $ 1

) f: A → B, g: B → C h: + → D

: (fg)h=f(gh). 0 ) ) A

) ) 1A: A → A42, *

« »: 1Af = f g1A = g f: A → B g: B → A. 9 , ) )

43 – # Set.

Set.

) 6 Set, )

) – '. ) A %

6 (' % 6) Set,

) B * ) A → B (B → A). ' , Set 2

) , % 2 )

1 ).

) f: A → B :

', ) g, h: + → A

gf = hf g=h () * f ); 2 ', ) g, h: B → C

fg = fh g=h () * f );

', f – % 1 %;

', ) g: B → A

fg = 1A gf = 1B;

2 ', A=B;

', f – % 1 %.

414 S M set ()) map ()).

42$ , 1 = .

43* .

44

. 1. 4%

, ) 2,

% % Set.

1. $ % f: A ® B, A¹Æ, 2#4 :

1)f – 6;

2)f – ';

3)4 'k: B ® A, fk = 1A;

4)# *u: A ® + v: C ® B : f=uv, u –

'.

! , " 1) 3) 4) 2) 1).

1) 3). , ) f 2 a – %

1 A, ) k: B ® A %

x, f (x) = b k(b) =

a, b Î B \ Im f .

3) 4). $ 3) f=uv

u: A ® + v: C ® A. % g, h: D ® A,

gu=hu. + g=g1A=gfk=guvk=huvk=hfk=h1A=h.

4) 2). 0 , f=f1B.

2) 1). $) , % f

2. A * 1 a1¹a2, f(a1)= f(a2). ) C

) g, h: + ® A, g(+)={a1} h(+)={a2}. +

g¹h, gf = hf. $ .

/ 1. 0 fg – 6, f – 6.

/ 2. 1 % * (* 4 *) 6 %6.

2. $ % f: A ® B44 2#4 :

1)f – # 6;

2)f – 2 ';

3)4 'k: B ® A, kf = 1B;

4)# *u: A ® + v: C ® B : f=uv, v – 2 '.

! , " 1) 3) 4) 2) 1).

44 , B , A f= . 0 f 1)–4) . $1 ) , B .

45

1) 3). ! 2 f

{f-1(b): bÎ B} ) A. $

) f-1(b) 1 b¢. ) k: B ® A, k(b)=b¢

bÎ B kf = 1B.

3) 4). $ 3) f=uv

u: A ® + v: C ® B. % g, h: B ® D,

vg=vh. +

g=1Bg =kfg=kuvg=kuvh=kfh=1Bh=h.

0 4) 2) , f=1Af. 2) 1). $), f 2. + B\Im f ¹ Æ.

) C, ) * 1 c d.

) g, h: B ® C, * Imf ,

g(B\Im f)={c} h(B\Im f)={d}. 0 fg=fh, g¹h. (, f

1 %. - .

/ 3. 0 fg – # 6, g – # 6.

%#4 :

1)f – ;

2)f – ';

3)f – ';

4)f=uv, u – ', v – 2 '.

1 2 , fg = 1A

hf = 1B g=h g, h: B ® A. , fg = 1A

hf = 1B,

g=1Bg=(hf)g=h(fg)=h1A=h.

. 2. $ % 1 %

) , %

% %

* %

( ). 0 % 2, ) 3), 4) 1 2 . ,

) ,

). 1

. 4.

3) 4) 1 2.

4. $ # A # %

n 2 :

46

1)A =n;

2)( ) ' % 6 X

4 n 'X → A;

3)6 A nn 2 ';

4)6 A n! '.

5

4. 4. 9 1944 . 4. [3, 8, 13, 18, 19, 23]. + )

.

αβ M(A, C), 'α β.

3.% ,

: α M(A, B), β M(B, C) γ M(C, D), (αβ)γ=α(βγ).

4.# ) 2 A Ob

'1A M(A, A).

5. 0 2 A, B, + Ob %

α M(A, B) β M(C, A) 1Aα=α β1A=β. $ 1

). % α M(A, B) α: A → B (

)) 47 2 A 2 B. 4% )

% 2 %

. . )

2 (* )), %- 2, 2 . . ) !

% – «)» ) ,

45C, Ob, M category ( ), object (2) morphism (%).

46$ , M(A, B)ÇM(C, D)=Æ, A¹C B¹D.

47+ . 4. 9 !

.

47

* . $

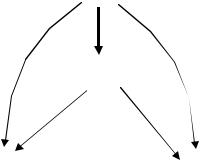
2 2.

. 6 6 X Ob % A → X M. $2

α: A → X β: B → X 2 X %,

* % γ: A → B, γβ=α. ;,

! % 2 1

2 2 X .

%. 4 , 2 2

% ) 2,

% 2 - ,

% 2.

6A, B Ob 2

A×B Ob % π1: A×B → A, π2: A×B → B ,

2 C Ob % α: C → A, β: C → B * % γ: C → A×B,

* γπ1=α γπ2=β. 9

) :

, ) ) π1 π2

: π1((a, b))=a π2((a, b))=b

a A b B.

- ) Set.

.

*. 1. # : 2 ) )

, % – % .

2. # )

) %.

48

3.#

) ) .

4.' ( ) ) X ! ρ ) 48, 2

) 1 ) X a, b X

5. $ A

( ) 2 A

.

2., (%) 2

%, . . * %

) .

3.$), % A → B % 2 A %. )?

4.0 ), %

(1 %, %) %

(1 %, %).

5.$), % %.

6.$ α: A → B – % . +

% β: B → A, αβ=1A βα=1B,

. 0 ) 1.

7.0 ) ): αβ – %

(1 %), α – % (β – 1 %).

8.$), 2 A

) M(A, A) % .

9.0 ), - 2

( ) 2 ) 1

) ).

10.Set 1

).

11.2

2, Set

* 2 2 ).

48 # , 2 ).

49

. 3. 60-70- XX . . '

(1 ), 1 Set. + ,

- -)

. + ) , «1» 2,

2 !

, (%) . +

49. , % %

.

# 1

1.! . +. ) *

. – .: . , 1977. – 368 .

2.! * %!. . # ). – .: - -

&, 1988. – 112 .

3.' "., . 4 . – .:

, 1976. – 400 .

4.(., $ !.

%. – .: , 1972. – 260 .

5.. + ). – .: , 1965. – 456 .

6.0. . . – #: - -

&&, 2004. – 215 .

7.. ). –

.: , 1983. – 152 .

8." . +. # . – .: , 1983. – 488 .

9." 2* ., 1 $., . -. # .

%. – .: , 1998. – 704 .

10.9 * . + ) %. – .: , 1973.

11.1 $ . * . – .: . , 1981. – 432 .

12.1". + ). – .: . , 1985.

13.1 . . – .: , 1968. – 352 .

14.1 2 . + ) - . – .: , 1969. – 348 .

15.1 $., ". # . – .: . , 1990. – 384 .

50