Основные структуры классической математики

$ 9. , f ± % )

) X , x ≤ f(x) x X. 9 )

' / , ) %

. + 5 9

4 ( , ) ).

5±9

) [27]. +

[1, 2, 7, 8, 17, 20, 21, 27, 34].

0

( X. 0 1 X ' %

± 1 ) {x X: a < x}, a X,

(a, b) = {x X: a < x < b} a ≤ b X.

& 1. $ X, ≤ ± . ,

% X X,

% . ) X

.

10. :#

(* ') %.

11. 1 %

X 2 X.

/ 1. , % 2

* .

/ 2.

% % ,

%. 2.

., 1 a ≤ b X [a, b] = {x X: a ≤ x ≤ b} X a b. ,

* ) .

12. + % X

% , %X .

$ . 10. $),

X ,

) ! 1 X * 1, ) ! 1 * 1.

+ %,

).

141

11.4 X 1 * X X

). 0 ) 1. + )

%.

12.0 ), Y

, * ,

Y. $ * . - ) ,

. %

) [37].

0 10 (" %, 1948 ) [1, . 183][5, . 315]. + 11 (#ë , 8, 1910 )

[1, . 248] [5, . 315]. 0 12 ) [5, . 316].

("

.

0

) 10 )

. , , *

) 1 Z,

, *

.

13. 1 % X '

#4 * Z * :

{1, 2, …, n}, X %.

%. 2;

% N, X %.

2, %. 2;

* % * * ,

X %. 2, %.

2;

Z, X %., %.

2.

! , ". $) , X

! 1 a1. , X 1, a1 * * 1 a2. $) ,

A a1 < a2 < ¼ < an < ¼ . , X n 1, 1 n- , ,

X % {1, 2, ¼ , n} . , X

, A % N. ' , X

142

A: , ) B = X\A ,

(A, B), , A !

1, ).

4, X ! 1,

! 1,

: X % .

., X !, !

1, 1 a0, (

!) ¼ < a-m < ¼ < a-2 < a-1 < a0 < a1 < a2 < ¼ < an < ¼ ,

* X % Z.

$ 13. 0 ),

, ) 1 a < b *

a b, ) 1

.

"

$ ) )

- . * .

/ $ ,

. / .,

.

0, ) S

,

) S. . , ) ) )

. 4 ), 1,

)

(* ). $ , * #,

1.

14. $ % X 2 #4

:

1)X .;

2)X $ ;

3)X 1;

4)X ;

5)%X , X .

! , ". 9 1), 4) 5)

12 1 11. $1

1) 3) 2) 1).

143

1) 3). $ X ! S ±

) . ) A

S

) . $ , sup A )

S.

3) 2). $ X # (A, B) ±

X. ) )

[a, b], a A b B. . (, * 1 c X, ) * ) ! .

, c ) (A, B).

2) 1). $ X 0 Y ± -

) X. ) B

) Y ) A = X\B. 4 (A, B)

1 * ,

.

15. # % % # %

* * #4 * * (inf sup).

16. % %

%. %. 2 ' R. /. :# % %'

%R.

$ 14. ! %

. $), 20

*. 0 1 R2

% : (a; b) < (c; d) , a < c

b < d a = c. $ ,

! ! 1, . $ 15. 0 ), %

.

+ 15 * 0 1881

( . [20, . 218]). 0 16 [1, . 56] ( .

) [17]).

# 2 N, Z, Q R !

(N), ) (), R )

144

, . [7]) . 0 N * $ . 4 Z Q ± 1

, ) * N Z

. R

.

, )

:

. 4 13, 2 16 ( )

* .

& 3. + N % *

( ) , * ! 1,

* ! 1.

& 4. + Z *

! ! 1.

& 5. + Q % *

! ! 1.

& 6. + R % *

, * !,

! 1.

.. 1 « » , N, Z, Q R ) %

. . N ) )

. 5 Z % «

». 0, Q )

Z, R ±

Q.

% * ). $ . 16. 0 ),

) X :

1)X % N;

2)X ± ), )

) ;

3)X ± ), )

) ! 1. 4. ) $) I.

17. , % Z ,

% % N,

% N.

18. $ ) Q % Q?

145

19. 0 ), X ! !

1 1 ):

1)X % R;

2)X , ,

) X .

20. 0 ), P %

R , P

%

*.

3.5. 1 . & 1

#

& 1. ),

1 ) ,

..

. ! L ) +

) × %:

a+b = sup(a, b) ab = a×b = inf(a, b). ( )

$ L, +, × , *

):

1)a+b = b+a, ab = ba ( );

2)(a+b)+c = a+(b+c), (ab)c = a(bc) ( );

3)a+a = a, aa = a ( );

4)a+ab = a, a(a+b) = a ( *).

$ 1. 0 ), L, +, ×

1)±4).

& 2. 5 L, +, ×

) + ) ×, *

1)±4) , ..

1 !,

2 ± .

$ ! L, +, × .

L ! £ %:

a £ b a+b = b (1, ab = a). ( ) $ 2. $ , ! £

146

$ 3. $), ( ) ( )

* ) !

1 2 ( ) L).

$1 ! , !

L, +, ×, £ , * £,

+ ×, ! ( ), ( ) 1)±4).

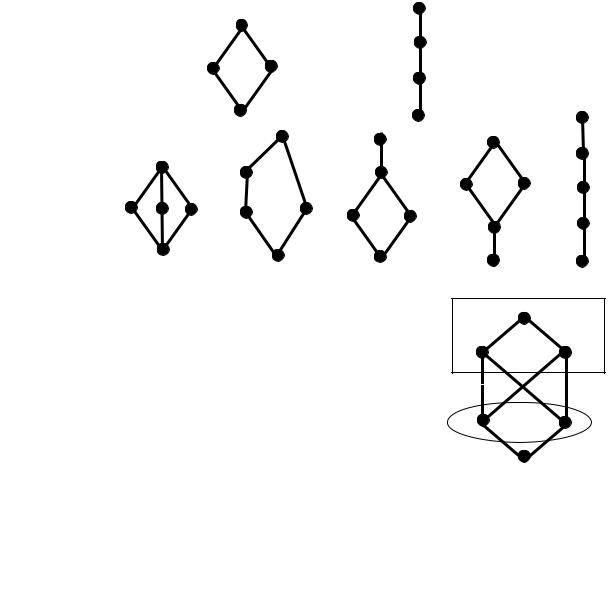
, m-1 ! (m ³ 3) !

! 1, (m±2)-1

). + ) !. $ 8 ! * m = 4 5.

($ m £ 3 -, - 1 .)

m = 4

147

5.0 ), ! )

): a ≤ b c ≤ d a+c ≤ b+d ac ≤ bd.

6., ! )

(ab+ac)(ab+bc) = ab.

7. $), !

ab+ac ≤ a(ab+c) ≤ a(b+c).

8. .! 1 !

0, ! 1 !

1. 0 ), 1 0 ( 1 1) !, *,

) 0a = 0, 0+a = a ( : 1a = a, 1+a = 1).

# , !

!, 1, %- !, % .

#

& 3. .

), )

) .

' ! L ! 0 = inf L

1 = sup L.

) !:

1)[r, s], r, s R r < s;

2)B(M) ) M;

3)!;

4)! N0,

! ;

5)! ;

6)! ) 1

! ;

7)! ( ) )

.

&, ) f: X → X ) X

# x0 X, f(x0)=x0.

) ) )

) !. 0 )

:

148

1. f #

. L * # .

! , ". L )

A={xÎL: x£ f(x)}.

$) x1=sup A. $ 0ÎA, sup A *. $),

f(x1)=x1. + x£ x1 xÎA, x£ f(x)£ f(x1) xÎA. $1 f(x1) ± ) A, x1£ f(x1).

f(x1)£ f(f(x1)), . . f(x1)ÎA. (, f(x1)£ x1.

(, x1 ! )

) f. .! ) x0 ) f

:

x0=inf B B={xÎL: x³ f(x)}.

)

F(f)={xÎL: f(x)=x }

) ) f AÇB. $ 9. $), ) F(f)

! ! L.

), ! ,

+ (+, 01, 1955 ). $ 10. )

01 . $ * .

2 (4. . #, 1982 ). $

F . L *

* f: L ® L,. . F=F(f), * , F

. % .

! , ". * %. $ F=F(f)

) f ! L . .) ,

) F, £ , £ ! L,

. $ F ! 1 x0,

( ?), ) XÍ F F

. ) Y

F ) X. , ! 1 x1. $) s=sup X t=inf Y L. + s£ y yÎ Y, s£ t.

149

) ! [s, t] . $ 1

* 1 pÎ [s, t]ÇF. $ s£ f(s)£ p£ f(t)£ t. $1 pÎ Y t£ p. - t=pÎ Y ! 1 Y, . . t=supF X.

$%. ! L, £ )

FÍ L, * ! £. .)

) f: L ® L, F=F(f). $

x1 ± ! 1 ) F. $

+ f ) L F F(f)=F. 0

) f L 1 x< y ), f(x)£ f(y).

) :

1.y£ x1. + {aÎ F: y£ a}Í {aÎ F: x£ a} , , f(x)=inf {aÎ F: x£ a}£ inf {aÎ F: y£ a}=f(y).

2.x£ x1, , y£ x1. + f(x)£ f(x1)=x1=f(y).

3.x£ x1 y£ x1 . + f(x)=x1=f(y). + .

(, *

$ 11. . ),

) f g . 5 f=g? #

L F * )

h: L ® L, , F=F(h)?

$ , )

) ( . [35]). $ 12. 0 ), )

) . 9

" 1:

) n- ) .

150