
Основные структуры классической математики
.pdf1)) %;
2)) ± %,
#4 * ;
3)# ) #
#4 # %.
! , ". , ) 1) 2) 1, 3) 2). $ )
) 1). @ ) ) Y. )
) 1 x1,¼ , xk,
1 ! . $1 Y *
1, ! 1 ,
), x1. $ )
), 1 y1 Y , ! x1. $)
, Y
* 1.
(, )
#,
#, ) % :
. 0
* * , .
), 1
) 2) 3) # [5, c. 237, . 7].
. #
2 * * %
% %
, 2 ,
# %.
! , ". ) 1 2 ,
) ) Y
)
. $) , X ×Y *
A. ) 1 ! (
) ) ±
) )
, *
Y. $ ) 2,
1- ! * x1 < x2 < ... < xn < ... .
0 * ) {(xn , yn ) } !. # !, ) 1 yn
* .
131
! 1. $
! .
/ 1 ( 0).
% * * %
%.
..
) *
. ),
, ± 1
), . $1 # ,
, #4
% %, .
/ 2.
* % ,
2 # # %
( . . # ),
# # %.
3.3. ' ( & ! )4
), * 8. ,
)
8.
& 1. 4 ), ) X
) ( )),
< . : a, b X a< b , X *
1 x0 = a, x1, ¼ , xn = b, , xi+1
xi ) i= 0, 1, ¼ , n±1. $ 1 ,
a b.
0, ) X
) {x X: a ≤ x ≤ b} a ≤ b.
), ,
% . ' )
8.
! 8 )
, 1. .
) 8 )
( ),
132
1. ) X 1 £
1 ³
1. (, ) 1 X, *
, , ) ) *
1 X. 0
) 8 1, * ,
. . , Z
! 8,
! ! 1. # )
8 X?
$ X ± )
8. X - X0, * /. 0 ) 1 aÎX\X0 * 1 bÎX0, , a b
b a. 9 X, ! (!)
1 X0, ) X+ ( , X-). ( ) 1 ) )
. , X- = Æ, X 8, *
) X0 1. , ) X+ = Æ,X 8, * ) X0
1.
+ ), ) X- X+ . + X X-, X0, X+. 0, ) X- X+ ± ! 1 aÎX b, cÎX0, b < a < c,
1 b c X0, ). . ),
1 X- 1 X+.
) X+ X1, X2,¼ , Xn,¼ ,
) . 5
) X- X-1, X-2,¼ ,
X-m,¼ .
*. 0 8
) ) .
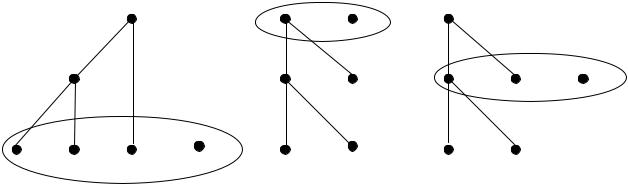
) X = {a, b, c, d, e, f}, a < e < f, b < ec < f. $ ±
) 1 X1 = {a, b, c, d},
X2 = {e} X3 = {f} ( . 1).
133
|
|
f |
f |
d |
|
f |
|
|
|
|
|
|
|
X0 |
|
|
|
|
|
|
|
|
|
|
e |
|
e |
c |
e |
c |
d |
|
|
|
|
|
|
|
|
a |
b |
c |
d |
|
|
|
|
|
|
|
a |
b |
a |
b |
|
|
. 1 |
|
. 2 |
|
|
. 3 |
|
0 ) 1 {d, f} {c, e}, {a, b} ( . 2). . ,
X0 = {c, d, e}, X1 = {f} X-1 = {a, b} ( . 3).
X * * : {a, b, c, d} {d, f}, )
8 ( . 1 2). 0 )
8
, ±
) 1 )
1 .
. ) ) X
* ( ),
X ( , ) ),
, , . , a < b ±
X, 1 a . #4 1 b, 1 b #4 a.
. +
0
Q. + (A, B) ( ) A½B) X
X A B (AÇB = Æ AÈB = X),
a < b aÎA bÎB. $ 1 ) A
(A, B), B ± * .
9 c X , , (A, B), a £ c £ b a ÎA b ÎB. 4 0, 1
2 ).
4 (A, B) X, * ),
4 %#: ) A ! 1,
134
B ! 1. 4 (A, B)
, ): A *
! 1, B ± !. 4 (A, B)
) : A ! 1 B
! 1.
& 2. / X
, X .
,
) ! 1 *
1, ! 1 *
1. . ) Z . 4
%
) ( 13 3.4).
* 1. % % )
% , .
! , ". 0
. $ X 8. X
(A, B). , ,
1 A 1 B; .
- ) 1 ,
) 8
, . .
).
1. $ # X, ≤ 2 #4 :
1)X );
2)X ), ( .)
% % ;
3)% X );
4)X ;
5)X .
! , ". - 1) 2) !. $ 8 ,
2) 3). $ ) 1 3) 4) 1 4) 5).
., X 5). X 1 a < b. , , ) 1 a b * 1 c1. ,
a < c1 < b , )
1 c2. $) 1 , !
135
,
(cn) X,
. 4, 1 a 1 b,
! .
) f: X → Y )
, a ≤ b f(a) ≤ f(b) a, b X. ( K )
( ) )
, X K * ) X
) Y, Y K. ' ,
) 8
),
) ( ,
, , )
1 ) *).
3.2 ,
)
. $
.
* 2. (Xi)
* ) %
, Xi # ) * (
) # .
! , ". $ X
) Xi 8. # ) Xi 8, % )
X, , i- , %. $)
, * Xi, *
. + ) Xi ai < bi, )
Xi ± 1 ai = bi. $ (ai) < (bi) X, 1 (ai)
1 (bi).
$ )
8 8. $1
,
) 8
8. $ X, Y ±
) 8 (a, b) < (c, d)
X×Y. ,, ), a = c, b < d Y
(a, b) < (a, d) X×Y. $1 ) ,
136
* |
a < a1 < ¼ < am-1 < c |
b < b1 < ¼ < bn-1 < d X Y . . |
|
(a, b) < (a1, b) <¼ < (am-1, b) < (c, b) < (c, b1) < ¼ (c, bn-1) < (c, d) |
|
(a, b) < (c, d) X×Y. |
$) . |
- ! * )
2. 1 * *
) , %
* % * *
.
( ),
) ,
) %
) .
3.4. )#' ( & !
0
), ) . / ,
, ! ). .
), ,
), ), . ) !
). +,
),
. $
. 4 *
), ,
* , % ,
, [1±3, 5±8, 11, 14±17, 20, 21, 25, 28, 33, 34, 37, 40].
/ ±
1 )
.
. ,
. $ ! % ,
! ) [14, 26]
[29±32], ) ) . 0 !
) )
.
137
!
$ X ± . , a < b X * 1 c X a < c < b, ! a < b
, 1 a ± 4 b b ± #4 a.
9 , * 1,
%. / , ;
) 1 a < b )
1. $) A X X,
) 1 a < b X
1 A. / * ( ),
) sup ( , inf).
, . /
*,
) sup. 0
, )
. $ . 1. 0 ),
, ! 1. 4% ).
2.0 ), ,
.
3.$ ,
!.
4.,
% .
4% .
1.
%, 4 , . 2
* # 4 * *
.
0 * )
) X ,
! * ) X,
* .
2. :# %' Q
* % * ( %.,
%. 2), * % *
% * ( %. 2,
%. 2), * % *
% * ( %.,
138
%. 2), * % *
[0, 1] ( %. %. 2).
/ 1. %'
%Q.
/ 2. 1 %
%, ' # Q.
- 2 *
- :
3. *
%. %. 2 , . . #
' ,
.
$ 5. 0 X *
): X ;
X 1 * X. $ .
0 ( , !)
-$2 (1955 ).
4. $ % , *
, #
# .
$ ) [5±7, 10, 15, 16, 19±22, 24, 25, 27, 28, 36, 37]. + 1
6 1930 ;
[42]. + 2 ) #; )
[5, . 262], [20, . 222], ) [17]. 0 3,
' %, ), , [23],
4.1.3. 0 4 [27, 3 § 3 15 § 4].
*
) !
). *
,
, %
.
/ N
). ' )
) . ; ),
) . $ . 6. . N.
139
7.0 ),
) ,
( ) * .
8.0 ), ),
* 1 (!),
% N.
- (/, 1904 ) *
5 ( ;, 1904 ).
%.
;, / . - ), 1
. - , /,
*
).
6 ( % ) ', 1914 [34]).
:# %%
% .
7 ( ;, 1935 ). 0
% *,
% 2.
$ Y X ' % X,
x X * y Y, x ≤ y.
) * ) ( ,
4), ) *
.
8. % ' %
.
% X ) {x X: x < a}, a ± 1 X. -
* .
9. $ # * * X Y
% #4 * :
1)X Y ';
2)X ' % Y;
3)Y ' % X.
+ %, * ,
% . 5 %,
1 ,
* ):
140
