§4. Комплексные матрицы.

Матрица может быть составлена не только из действительных чисел, но и из комплексных чисел тоже. Будем называть такие матрицы комплексными. Заменим в комплексной матрице A все числа на комплексно сопряжённые. Получившуюся матрицу обозначим A; ¯.

Примем без доказательства, что detA; ¯ = detA; ¯¯¯ .

Операции сложения матриц, умножения матрицы на число (комплексное) и умножения двух матриц определяются дословно так же, как и для действительных матриц. Также имеет место равенство detAB=detA·detB.

Определение. Матрица S; ¯^T называется сопряжённой к матрице S и обозначается S^*. Матрица называется унитарной, если S^1=S^*  SS^*=E. Матрица называется эрмитовой, если C^*=C.

Эрмитова матрица – это аналог симметрической матрицы для действительных матриц, а унитарная – аналог ортогональной. Для элементов эрмитовой матрицы должно выполняться сj; i=с;¯j; i, i,j=1, 2,…, n.

Для элементов унитарной матрицы сумма модулей элементов одной строки равна 1, а сумма произведений элементов одной строки на сопряженные числа к элементам другой строки равна нулю:

(;\s\do12(i =1sj; is;¯m; i=_jm, j,m=1, 2,…, n.

Кроме этого det(S; ¯^TS)=detS; ¯^T ·detS=detST; ¯¯¯·detS= detS; ¯¯¯·detS=|detS|². Отсюда detS=1 (в точности, как для ортогональных матриц).

Примеры эрмитовой и унитарной матриц:

, .

Глава 3. Векторные пространства

Мы уже видели, что операции сложения матриц и умножения матриц на число обладают в точности такими же свойствами, как и операции сложения векторов и умножения вектора на число. Это говорит о том, что с точки зрения алгебры, множество всех векторов и множество всех матриц фиксированного размера устроены одинаково. Поэтому мы можем матрицы тоже назвать векторами и изучать их свойства одновременно со свойствами геометрических векторов, при условии, что доказываемые результаты опираются только на свойства линейных операций. Кроме того, такими же свойствами обладают линейные операции над функциями и многими другими математическими объектами. Это приводит нас к необходимости ввести понятие, обобщающее все возможные множества математических объектов, которые можно складывать и умножать на число.

§1. Векторное пространство. Линейная зависимость векторов

Определение. Пусть L – произвольное множество, для элементов которого заданы две операции: сложение элементов и умножение элемента на действительное число, так что x, y, z L и , R выполнено x+yL, xL (т.е. операции не выводят за пределы L), и при этом имеют место следующие аксиомы.

А1. x + y = y + x (коммутативность сложения);

A2. (x + y) + z = x +(y + z) (ассоциативность сложения);

A3.  o  L такой что x + o = x (существование нулевого элемента);

A4.  (–x) L такой что x + (–x) = o (существование противоположного элемента);

A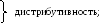5.(x + y) = x + y

A6. ( + )x = x+ x

A7. ()x = (x) ;

A8. 1·x = x .

Тогда L вместе с данными операциями называется линейным или векторным пространством. Элементы этого пространства будем называть векторами.

Примеры. 1. Пространство V², состоящее из всех геометрических векторов на плоскости, или V³, состоящее из всех векторов в пространстве. Тогда А1 – A8 представляют собой свойства операций над векторами. Эти свойства мы доказывали в главе 1.

2. Арифметическое пространство R³, элементами которого являются тройки действительных чисел, которые могут быть записаны в виде строки или столбца. Мы будем записывать эти тройки в виде столбца:

R³ = x₁, x₂, x₃ R .

Операции в R³ определяются следующим образом. Если

X = , Y = ,

то

X +Y = , X = .

Необходимо проверить, что в данном пространстве выполняются аксиомы А1 – А8. Проверим, например, А5.

(X +Y ) =  = = + = X +Y.

Роль нулевого элемента и элемента, противоположного к X очевидно, играют столбцы

O = и – X = ,

т.е выполнены А3 и А4.

Упражнение. Проверьте самостоятельно, что выполняются остальные аксиомы.

Аналогично определяется арифметическое пространство Rⁿ состоящее из столбцов высоты n .

3. Пространство P_n , которое состоит из всех многочленов с действительными коэффициентами, степени не превосходящей n:

P_n = {a_o+ a₁t + a₂t² +…+ a_nt ⁿ | a_o, a₁,…, a_nR}

с обычными операциями сложения многочленов и умножения многочлена на число.

4. Пространство C^o([0,1]) , которое состоит из всех функций, непрерывных на отрезке [0,1].

Можно привести ещё массу примеров. Главное – уяснить себе, что векторное пространство может состоять из совершенно любых математических объектов, которые можно складывать и умножать на число, если, конечно, выполняются А1 – А8. При изучении дальнейшего материала, для простоты восприятия, можно представлять себе, что речь идет о геометрических векторах.

Из аксиом А1 – А8 можно вывести следующие следствия:

1) единственность нулевого элемента;

2) единственность противоположного элемента;

3) 0·x = o ;

4) –1·x = –x ;

5) ·o = o xL и R.

Определение. Пусть x₁, x₂,…, x_nL – произвольные векторы, а ₁, ₂,…, _n – произвольные числа. Тогда выражение

₁x₁+ ₂x₂ +…+ _nx_n (3.1)

называется линейной комбинацией векторов x₁, x₂,…, x_n. Числа ₁, ₂,…, _n называются коэффициентами линейной комбинации. Линейная комбинация (3.1) называется тривиальной, если все её коэффициенты равны нулю: ₁= ₂ =…= _n = 0. Соответственно, линейная комбинация (3.1) называется нетривиальной, если среди её коэффициентов ₁, ₂,…, _n есть хотя бы одно ненулевое число.

Определение. Векторы x₁, x₂,…, x_n называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевому вектору:

₁x₁+ ₂x₂ +…+ _nx_n = o. (3.2)

Соответственно векторы x₁, x₂,…, x_n называются линейно независимыми, если равенство (3.2) возможно только для тривиальной комбинации, т.е. когда ₁= ₂ =…= _n = 0.

Примеры. 1. Векторы i, j, k в пространстве V³ линейно независимы, а векторы a₁=i+j, a₂=i+j+k, a₃=k линейно зависимы, т.к. 1·a₁+(–1)·a₂+1·a₃ =o.

2. В пространстве R³ столбцы

E₁ = , E₂ = , E₃ =

линейно независимы. Действительно,

₁E₁+ ₂E₂ +₃E₃ = O  =  ₁= ₂ =…= _n = 0,

т.е. только тривиальная комбинация столбцов E₁, E₂, E₃ может быть равна нулевому столбцу. Если к столбцам E₁, E₂, E₃ добавить произвольный столбец X = , то получим линейно зависимую систему столбцов {E₁, E₂, E₃, X}, т.к.

x₁·E₁+ x₂·E₂ + x₃·E₃ + (–1)·X = O.

3. В пространстве P_n многочлены 1, t, t²,…, t ⁿ линейно независимы. Если к ним добавить любой многочлен f(t) степени n, то получим линейно зависимую систему.

Упражнение. Самостоятельно покажите, что функции f(t)1, g(t) = cos t, h(t) = sin 2t в пространстве C^o([0,1]) линейно зависимы.

Предложение 1. Векторы x₁, x₂,…, x_k (k>1) линейно зависимы, тогда и только тогда, когда один из них является линейной комбинацией остальных.

Действительно, пусть векторы x₁, x₂,…, x_k линейно зависимы, и

₁x₁+ ₂x₂ +…+ _kx_k = o –

их нетривиальная линейная комбинация, где, например, _k0. Тогда можем выразить x_k:

x_k = x₁+ x₂ +…+ x _k–1,

т.е. x_k является линейной комбинацией векторов x₁, x₂,…, x_k–1.

Обратно, если x_k = ₁x₁+ ₂x₂ +…+ _k–1x _k–1, то

₁x₁+ ₂x₂ +…+ _k–1x _k–1+ (–1)x_k = o,

икомбинация нетривиальная, т.к. –10.

Предложение 2. Если среди векторов x₁, x₂,…, x_k есть нулевой, то эти векторы линейно зависимы.

Действительно, если, например, x_k = o, то

0·x₁+ …+ 0·x _k–1+ 1·x_k = o,

икомбинация нетривиальная, т.к. 10.