С учетом формул (1.69)-(1.71) ротор вектора может быть записан в разложении по осям декартовой системы координат в виде

. (1.72)

В теории векторных полей доказано, что зная ротор вектора в каждой точке некоторой поверхностиS, можно вычислить циркуляцию вектора по контуруL, ограничивающему поверхность s:

. (1.73)

Соотношение (1.73) представляет собой математическое выражение теоремы Стокса. Таким образом, с учетом выражений (1.62), (1.73) условие безвихревого характера электростатического поля может быть записано как в дифференциальной так и в интегральной форме:

(1.74)

1.9.2 Градиент потенциала. Эквипотенциальные поверхности

Формула (1.59) позволяет найти разность потенциалов между двумя любыми точками поля, если известна зависимость напряженности от координат.

Решим обратную задачу, то есть по известной зависимости потенциала от координат определим напряженность электрического поля.

Э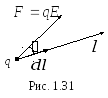лементарная работа сил поля по перемещению зарядаq в произвольном направлении может быть найдена двумя способами (рис. 1.31):

(1.75)

и как убыль потенциальной энергии (формулы 1.50и 1.53)

^.(1.76)

В выражении (1.76) использована частная производная отпоl,так как функцияв общем случае зависит от нескольких переменных.

Из выражений (1.75) и (1.76) находим соотношение

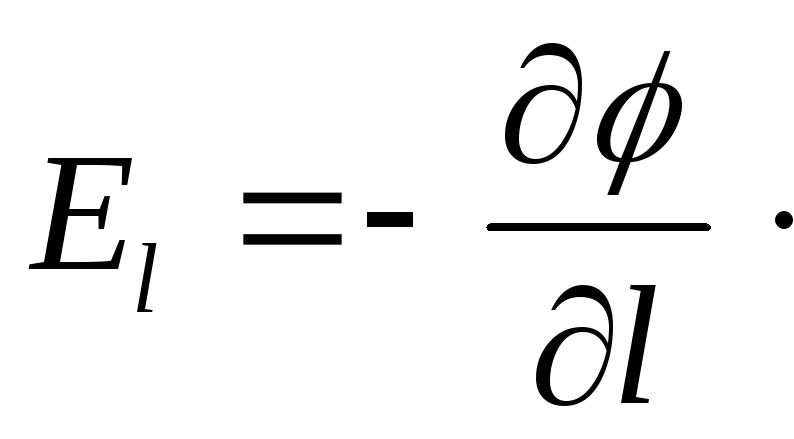(1.77)

Так как направление выбрано произвольно, то с помощью соотношения (1.77) можно найти проекции вектора, на оси декартовой системы координат

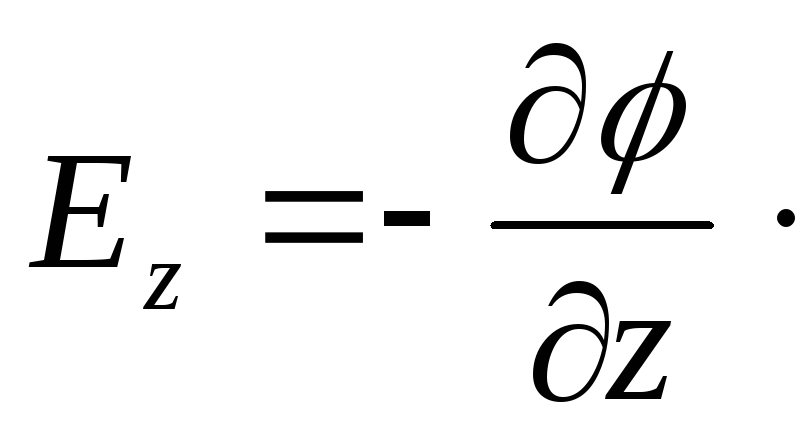; ;(1.78)

Вектор в разложении по осям декартовой системы координат имеет вид

^,(1.79)

где - орты декартовой системы координат. С учетом (1.78) равенство (1.79) принимает вид

(1.80)

Выражение, стоящее в скобках, называется градиентом скалярной функции и обозначаетсяgrad.

Используя понятие градиента потенциала, равенство (1.80) можно записать компактно

. (1.81)

Часто для обозначения операции gradиспользуют векторный дифференциальный оператор набла(оператор Гамильтона), который в разложении по осям декартовой системы координат имеет вид

(1.82)

Этот оператор действует на функцию, стоящую от него справа.

Из выражений (1.80), (1.81) и (1.82) следует, что

. (1.83)

Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком.

Градиент скалярной функции (х, у,z)- вектор, обладающий следующими свойствами:

1. Вектор совпадает с направлением, в котором скалярная функция, возрастая по абсолютной величине, изменяется наиболее быстро.

2. Проекция вектора на произвольное направление равна частной производной от потенциала по этому направлению

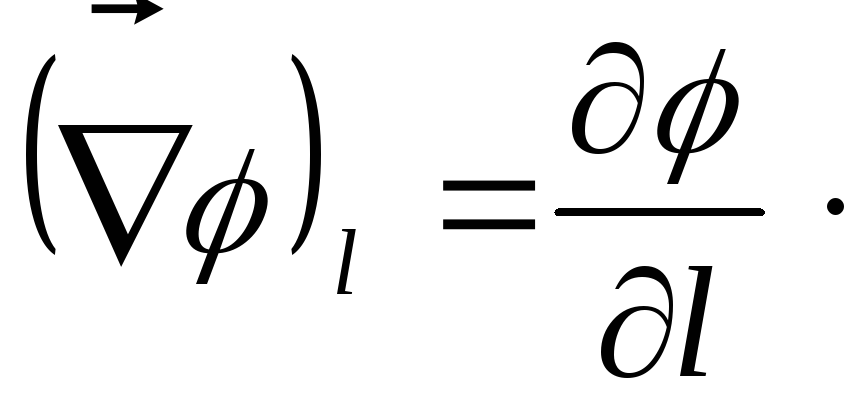(1.84)

Из свойства (2) следует, что если - единичный вектор, задающий направление вектора, то

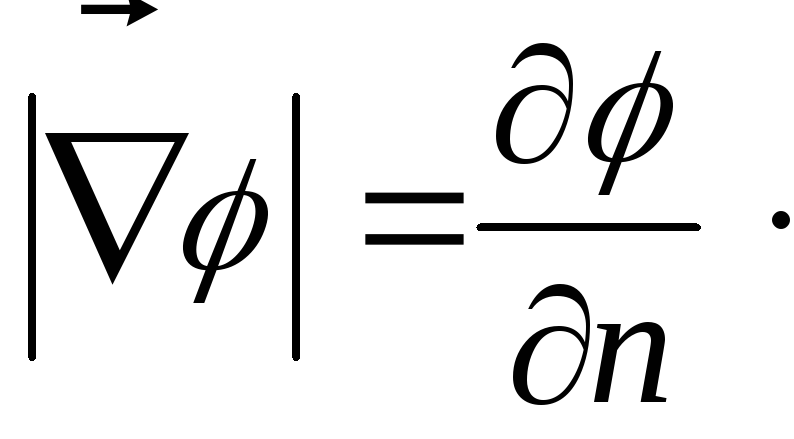(1.85)

Пусть единичный вектор задает направление перпендикулярное к, тогда из (1.84) следует, что

^.(1.86)

В качестве примера, поясняющего соотношение (1.83), рассчитаем напряженность электрического поля точечного положительного заряда (рис. 1.32) по известному выражению для потенциала:

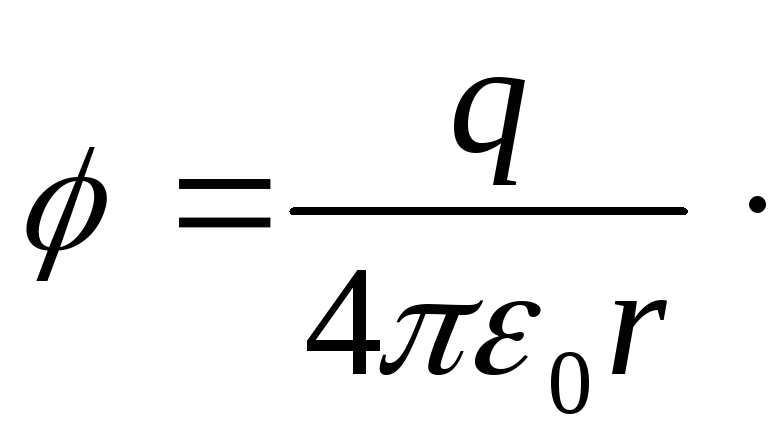(1.87)

И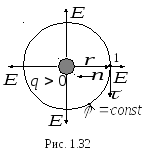з этого выражения следует, чтоповерхности равного потенциала (=const)-эквипотенциальные поверхности представляют собой концентрические с зарядом сферы(r = const). Одна из таких поверхностей показана на рис. 1.32. Определим направление векторав точке 1 эквипотенциальной поверхности. При смещении из этой точки в разных направлениях наdlфункция (1.87), возрастая по абсолютной величине, изменяется наиболее быстро в направлении от точки 1 к зарядуq. Следовательно, единичный вектор, задающий направление, может быть задан как

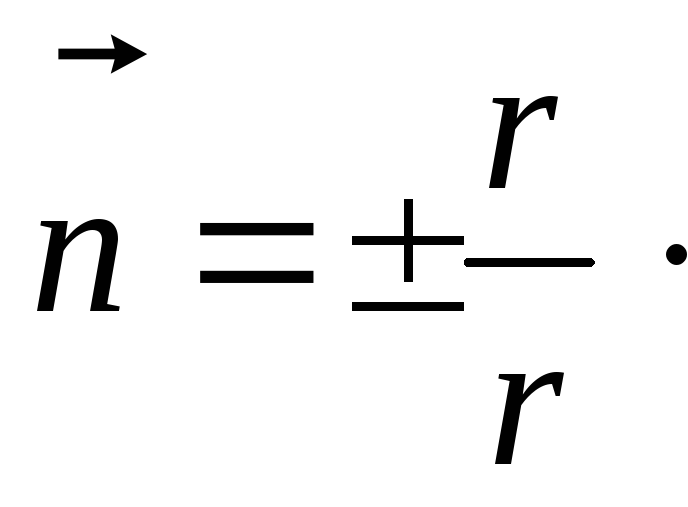(1.88)

где знак « - » соответствует положительному заряду, знак «+» - отрицательному.

Вектор можно представить в виде произведения его модуля на единичный вектор

. (1.89)

В соответствии с формулами (1.85), (1.87), (1.88)

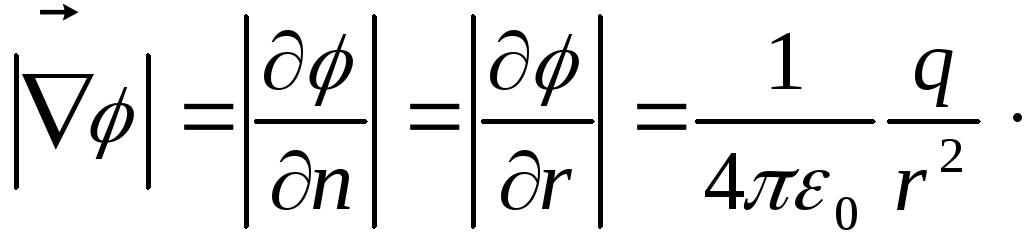. (1.90)

Подставив выражения (1.88), (1.89), (1.90) в формулу (1.83), получим известное выражение для напряженности электрического поля точечного заряда

.

Покажем, что вектор всегда направлен по нормали к эквипотенциальной поверхности.

Зададим с помощью единичного вектора направление касательной в некоторой точке 1 эквипотенциальной поверхности (рис. 1.33), а с помощью единичного вектора- направление нормальное к ней.

В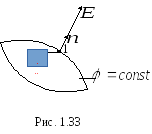екторможно разложить на составляющие вдоль направлений, заданных векторами и:

. (1.91)

При смещении из точки 1 на dвдоль поверхности потенциал не меняется, следовательно, из (1.77) получим

^.(1.92)

Из (1.91) с учетом (1.92) следует, что векторнаправлен по нормали к эквипотенциальной поверхности

. (1.93)

Так как вектор в каждой точке силовой линии направлен по касательной к ней, тосиловые линии напряженности в каждой точке электрического поля ортогональны эквипотенциальным поверхностям.

Электрическое поле можно наглядно изобразить с помощью эквипотенциальных поверхностей. Так как эквипотенциальную поверхность можно провести через любую точку поля, то условились их проводить таким образом, чтобы разность потенциалов - для всех соседних поверхностей была одна и та же.В тех областях поля, в которых эквипотенциальные поверхности располагаются ближе друг к другу, потенциал изменяется быстрее при перемещении по нормали к поверхности. Следовательно, в данной области поля больше, а значит и. Таким образом,по густоте эквипотенциальных поверхностей можно анализировать характер изменения напряженности электрического поля.