1.5. Метод силовых линий. Понятие потока вектора напряженности

Электрическое поле можно наглядно изображать с помощью линий напряженности (линии или силовые линии). Линии напряженности проводятся таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора(рис. 1.10, a).

Густота линий(число линий, пронизывающих единичную площадку, расположенную перпендикулярно к ним) выбирается равной модулю вектора(рис. 1.10, б).

По картине силовых линий можно судить о направлении и величине вектора в различных точках пространства.

Например, поле точечного заряда изображается с помощью радиальных прямых, направленных отзаряда, если он положителен, и к заряду, если он отрицателен (рис. 1.11, а). На рисунке 1.11, б приведена картина силовых линий диполя.

Важным свойством линий напряженности электростатического поля является то, что они начинаются и заканчиваются только на зарядах.Если рассматривается уединенный заряд, тоначавшись на положительном заряде, силовые линии уходят в бесконечность, либоприходя из бесконечности, заканчиваются на отрицательном заряде (рис. 1.11, а).

Электрическое поле, в каждой точке которого векторимеет неизменную величину и направление (т. е. выполняется условие(х, у,z)=const, называется однородным.Из определения однородного поля следует, что еголинии напряженности должны быть параллельнымии наносится с одинаковой густотой во всех точках поля (рис. 1.12).

На рис. 1.12 с помощью линий напряженности изображено поле плоского конденсатора. На рисунке видно, что в центральной части конденсатора поле однородно.

Одной из важных характеристик электрического поля является поток вектора через некоторую поверхностьS.

Поток обозначают , онравен числу линий напряженности, пронизывающих поверхность.

П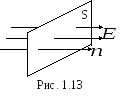олучим формулы для расчета потока в различных случаях. Рассмотрим сначала простейший случай, когда поле однородно и векторв каждой точке перпендикулярен плоской поверхностиS,т.е. векторпараллелен вектору нормали (рис. 1.13). В этом случае поток числено равен

. (1.18)

Если поле однородное, но ирасположены под углом(рис. 1.14), то для потока справедливо выражение

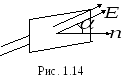, (1.19)

где Е_n- проекцияна направление нормали.

Если поле неоднородное и поверхность не плоская, то всю поверхность S можно разбить на элементарные участкиdS,в пределах которых векторможно считать постоянным (рис. 1.15). Затем вычислть элементарный потокчерез элемент поверхностиdS:

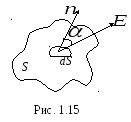
. (1.20)

Полный поток находим интегрированием выражения (1.20) по всей поверхности S:

^. (1.21)

Отметим, что поток является алгебраической величиной, знак которой зависит от выбора направления нормали. В случае замкнутых поверхностей принято вычислять поток, “вытекающий” из охватываемой поверхностью области наружу. В этом случае под положительной нормалью подразумевается обращенная наружу, т.е. внешняя нормаль.

1.6. Теорема Гаусса-Остроградского для вектора

Р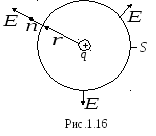ассмотрим сферу радиусаr, в центре которой помещен точечный зарядq (рис. 1.16). Вычислим поток векторачерез поверхность сферы.

В каждой точке поверхности сферы напряженность одинакова и равна

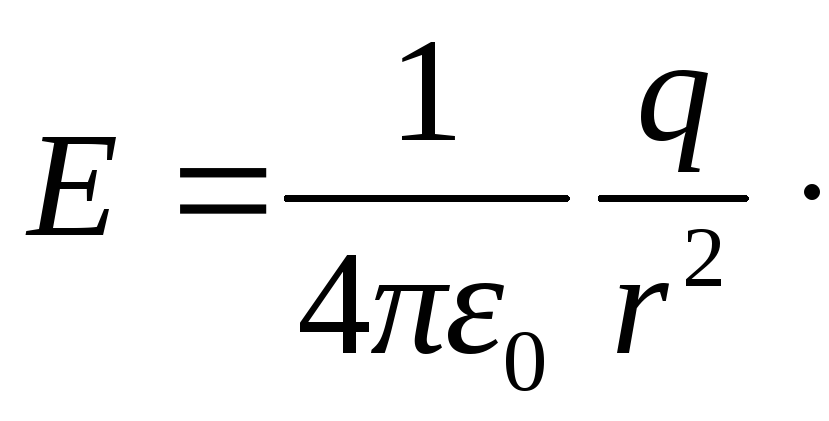(1.22)

Векторы ипараллельны, следовательно=E_n,т.е. модуль вектора числено равен проекции на нормаль. Согласно (1.21) поток через сферу равен

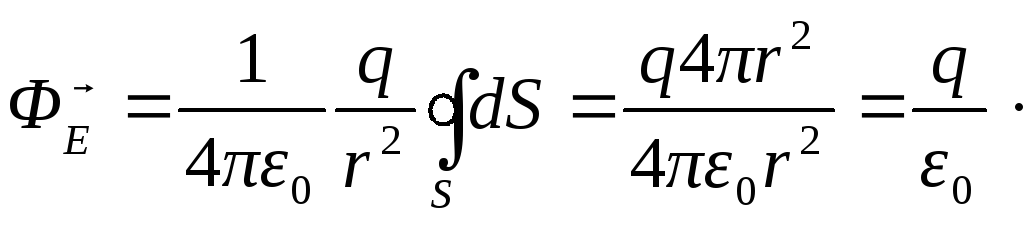(1.23)

Можно показать, что этот результат справедлив для замкнутой поверхности произвольной формы, т.к. число линий , пронизывающих её, неизменно.

Поместим внутри замкнутой поверхности N зарядовq₁, q_i, q_N. В силу принципа суперпозиции напряженность результирующего поля равна

. (1.24)

В этом случае выражение для потока приобретает вид

. (1.25)

Учитывая (1.23), можем записать

(1.26)

Если в объеме V, охватываемом поверхностью S, непрерывно распределен заряд с объемной плотностью =, то выражение (1.26) принимает вид

^. (1.27)

Выражения (1.26) и (1.27) представляют собой математическую запись теоремы Остроградского-Гаусса: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен суммарному заряду, охватываемому поверхностью, деленному на .

Из выражений (1.26) и (1.27) следует, что электрические заряды являются источниками электрического поля.

Частное от деления потока на объем, из которого поток выходит, определяет среднюю объемную мощность (заряд) источников поля в объемеV. В пределе, то есть при стягивании объема к некоторой точке Р, это отношение стремится к истиной объемной мощности источников поля, которую называют дивергенцией (или расхождением) вектора .

В соответствии с определением:

div(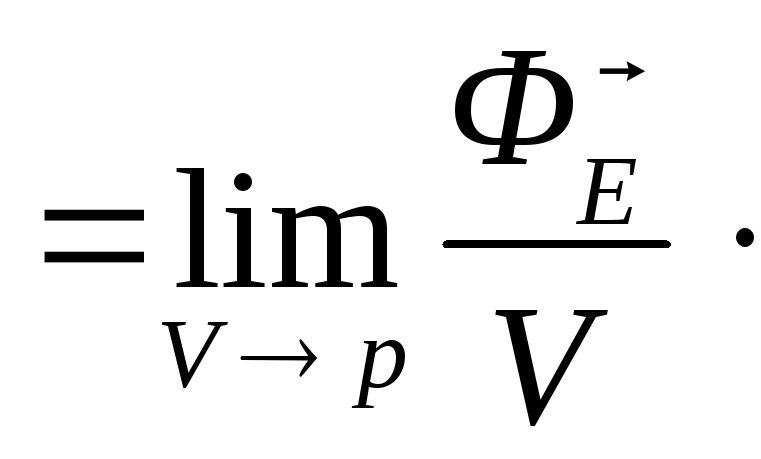1.28)

Найдем выражение для div, например, в декартовой системе координат. Поскольку форма рассматриваемого объема несущественна (он стягивается в точку), то удобно выбрать прямоугольный параллелепипед со сторонами Х,  У,  Z, параллельными осям декартовой системы координат (рис. 1.17).

Пусть в объеме параллелепипеда распределен заряд с объемной плотностью. Подсчитаем поток вектора через боковую поверхность параллелепипеда в виде суммы потоков через три пары противоположных граней. Поток через пару граней 1 и 2 (рис. 1.17), перпендикулярных к оси у равен:

, (1.29)

где учтено, что на грани 2 внешняя нормаль противоположна положительному направлению оси у.

Приращение составляющей напряженности в выражении (1.29) может быть представлено в виде

. (1.30)

С учетом (1.30) выражение (1.29) примет вид

, (1.31)

где  V = Х У Z – объем параллелепипеда.

Аналогично находятся потоки через пары других граней:

и . (1.32)

Полный поток через поверхность параллелепипеда равен

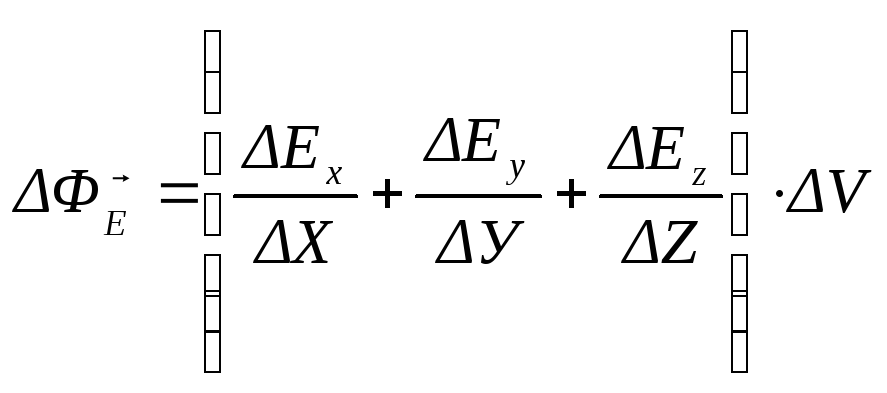^. (1.33)

В соответствие с определением (1.28) и выражением (1.33) находим дивергенцию вектора в точкеР (Х,У,Z):

(1.34)

Из выражения (1.34) следует, что , откуда для потока векторачерез поверхностьS, охватывающую объем V, находим

^. (1.35)

Заменив в (1.27) поверхностный интеграл в соответствии с (1.35) объемным, получим

^. (1.36)

Равенство (1.36) справедливо для произвольного объема, что возможно только в том случае, если значения подинтегральных функций совпадают в каждой точке пространства:

, (1.37)

Соотношение (1.37) является одним из фундаментальных уравнений электростатики и представляет собой теорему Остроградского-Гаусса в дифференциальной форме: дивергенция вектора напряженности электрического поля в каждой точке пропорциональна объемной плотности заряда в той же точке. Из уравнения (1.37) непосредственно следует, что заряды являются источниками электрического поля.