1.7.3. Поле бесконечного заряженного цилиндра (нити)

Пусть на поверхности заряженного цилиндра однородно распределен заряд (рис. 1.20 а).

Это означает, что отношение  = q / lимеет одно и то же значение для каждого элементарного отрезка l. Величину- называют линейной плотностью заряда (заряд, приходящийся на единицу длины нити).

Из соображений симметрии в распределении заряда следует, что в любой точке напряженность поля направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина Еможет зависеть лишь отr.

Построим коаксиальную с нитью цилиндрическую поверхность радиусом rи образующейl (рис. 1.20 а).

Для оснований цилиндра Е_n=0,поэтому поток вектора напряженности определяется только величиной потока через боковую поверхность цилиндра. Так как для боковой поверхностиr = const, то во всех её точкахЕ(r) = constи равнаЕ_n.Следовательно, для потока через боковую поверхность справедливо:

.

Внутрь цилиндра попадает заряд q =  l. Применяя теорему Остроградского-Гаусса, получаем

,

отсюда:

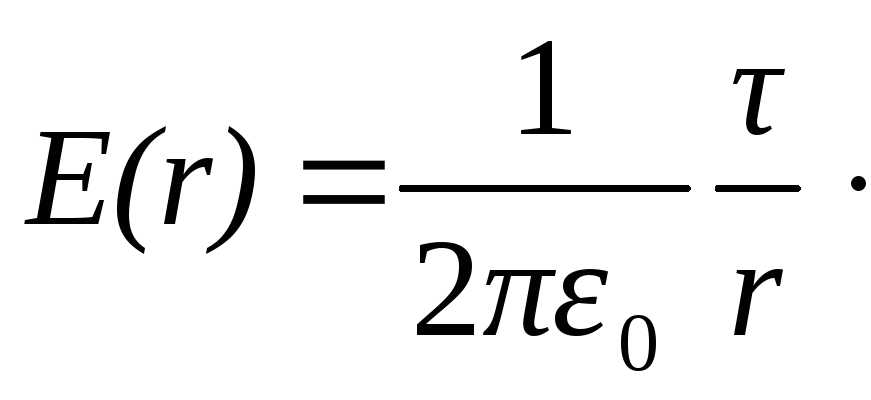(1.41)

С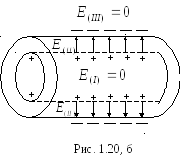помощью принципа суперпозиции электрических полей легко найти поле двух коаксиальных цилиндров, имеющих разные по знаку, заряды распределенные с одинаковой линейной плотностью (рис. 1.20 б).

Внутри меньшего цилиндра (область ) поле отсутствует. Этот вывод следует из теоремы Гаусса-Остроградского. Действительно, если коаксиально с меньшим цилиндром построить внутри него цилиндрическую поверхность, то внутри неё заряд равен нулю. Следовательно, поток вектораи электрическое поле будут равны нулю.

Вне большего цилиндра (область III) поле также отсутствует, так как через любую поверхность, охватывающую оба цилиндра, поток вектора равен нулю (суммарный заряд цилиндров равен нулю). Между цилиндрами (в области II) поле создано только зарядом внутреннего цилиндра и может быть рассчитано по формуле (1.30).

1.7.4. Поле заряженной сферы

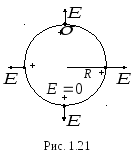
Рассмотрим сферу радиуса R, заряженную с постоянной поверхностной плотностью заряда (рис. 1.21).Из соображений симметрии в распределении заряда следует, что векторв любой точке совпадает с направлением нормали к поверхности, а величина напряженности является функцией расстоянияrот центра сферы. Построим мысленно сферическую поверхность большего радиуса(r > R). Для всех точек этой поверхностиЕ(r) = Е_n. Следовательно, применяя теорему Гаусса-Остроградского, получаем:

,

отсюда

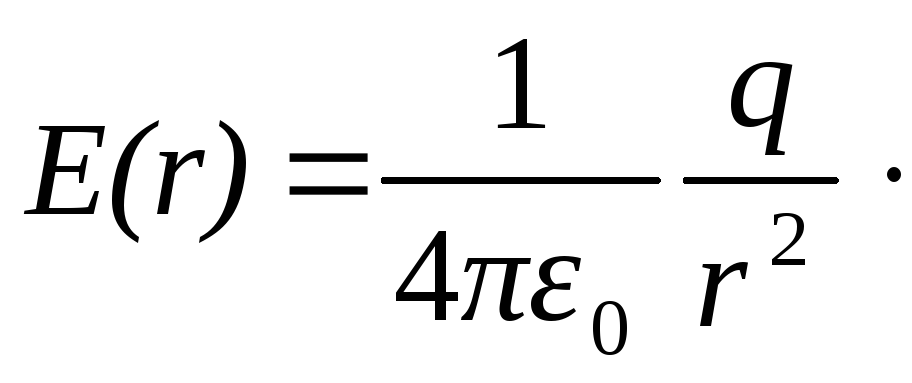
(1.42)

Формула (1.42) справедлива для всех точек, расположенных снаружи сферы. Аналогичные рассуждения, проведенные для сферы меньшего радиуса (r < R), показывают, что внутри заряженной сферической поверхности поле отсутствует(_внутри = 0).Сравнение формул (1.42) и (1.8) приводит к выводу о том, чтополе вне заряженной сферы тождественно с полем точечного заряда, равного заряду сферы и помещенного в ее центр. Используя принцип суперпозиции, можно показать, чтополе двух концентрических сфер, несущих одинаковые по величине и противоположные по знаку заряды, сосредоточено в пространстве между поверхностями и определяется формулой (1.42).