1.9. Связь между напряженностью электрического поля и потенциалом

Электрическое поле можно количественно описывать либо с помощью вектора напряженности , либо с помощью скалярной величины. Эти величины должны быть однозначно связаны друг с другом. Покажем как по известной функции (х, у, z) можно найти разность потенциалов между двумя любыми точками поля. Воспользуемся выражением для работы, совершаемой полем по перемещению зарядаq из точки 1 в точку 2:

^.(1.56)

Выразив силу через напряженность поля (формула 1.12), получим

^.(1.57)

Согласно формуле (1.54) эта же работа может быть представлена выражением

. (1.58)

Сравнивая эти две формулы, получаем

(1.59)

Таким образом, найдена связь между основными характеристиками электрического поля. Интеграл можно брать по любой линии, соединяющей точки 1 и 2, т.к. работа сил электрического поля не зависит от формы пути.

Применим формулу (1.59) для расчета разности потенциалов между двумя бесконечными разноименно заряженными плоскостями. Возьмем точки 1 и 2 произвольно на разных плоскостях и соединим их линией 1-1-2, как показано на рисунке 1.26.

Согласно формуле (1.59)

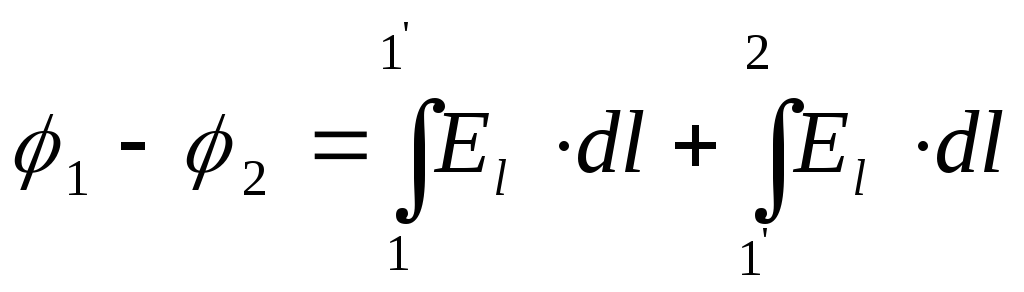, (1.60)

где Е_l- проекция векторана направление перемещения (рис.1.26 а).

На участке 1-Е_l= 0, поэтому первое слагаемое в правой части (1.60) равно нулю. На участке-2 для напряженности поля справедлива формула (1.39)

следовательно:

, (1.61)

где d - расстояние между плоскостями.

Этот результат справедлив для разности потенциалов между любыми двумя точками, взятыми в однородном поле, причемd в этом случае равно проекции отрезкаl₁₂между этими точками на направление вектора(рис. 1.26 б).

1.9.1. Теорема о циркуляции вектора напряженности электрического поля

При обходе в любом направлении по замкнутому контуру L (рис. 1.27)₁ = ₂,следовательно, выражение (1.59) приобретает вид

^.(1.62)

Скалярное произведение, стоящее под интегралом, указывает, что при расчете (1.62) надо учитывать уголмежду вектороми элементарным перемещением(рис 1.27), т.е. необходимо учитывать только составляющую вектора, касательную к элементам контураL.

Рассчитанный таким образом интеграл (1.51) называют циркуляцией вектора по любому замкнутому контуру L.

Из (1.62) следует, чтодля электростатического поля циркуляция вектора по любому замкнутому контуру равна нулю. Такие поляназывают безвихревыми или потенциальными. У векторных полей, для которых циркуляция не равна нулю, ее знак зависит от выбранного направления обхода контура при интегрировании.

Соотношение (1.62) установлено Максвеллом, его называют теоремой о циркуляции вектора и применяют для анализа свойств векторных полей. Например, из него следует,что существованиеэлектростатического поля такого вида как изображено на рис. 1.28 невозможно. Докажем это. Для этого рассчитаем циркуляцию вектора напряженности вдоль контура 1-2-3-4-1, представив контурный интеграл в виде суммы четырех интегралов:

. (1.63)

Второй и четвертый интегралы обращаются в нуль, т.к. на этих участках  , следовательно,= 90 и, соответственно,cos=0. Таким образом, получаем

^,

здесь учтено, что на участке 1-2 угол = 0, соответственно,cos= 1; на участке 3-4cos= -1, т. к. = 180⁰.

По густоте линий напряженности на рис. 1.28 можно заключить, что >. Поскольку участки 1-2 и 3-4 одинаковой длины, то значение интеграла на участке 1-2 больше, чем значение интеграла на участке 3-4. Следовательно,

^,

т.е.  0, что противоречит теореме (1.62).

Циркуляция вектора характеризует свойства поля, усредненные по области, ограниченной контуромL. Чтобы получить характеристику свойств поля в некоторой точкеРэтой области, необходимо площадьS,ограниченную контуром, стягивать к точкеР. Однако, при этом сама циркуляция обратится в нуль, так как длина контура в пределе обращается в нуль. Поэтому в качестве характеристики электрического поля в точкеР принимают предел отношения

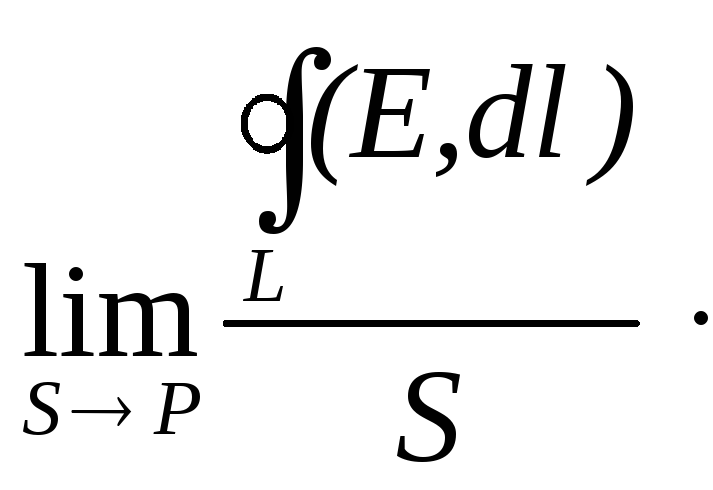(1.64)

П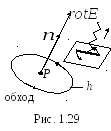ри вычислении предела (1.64) обнаружено, что еговеличина зависит не только от свойств поля в точке Р, но также и от ориентации контура в пространстве,которую задают с помощью положительной нормали, к плоскости контура.Положительная нормальсвязана с направлением обхода контура при интегрировании правилом правого винта (рис. 1.29).Изменяя положение контура в пространстве, можно обнаружить такую ориентацию нормали, при которой величина предела (1.64) окажется максимальной. Таким образом,величина (1.64)ведет себя какпроекция некоторого вектора на направление нормали к плоскости контура, по которому берется циркуляция.

Очевидно, максимальное значение величины (1.64) равно модулю этого вектора, а положительная нормаль, которая обеспечивает достижение максимума, задает его направление (рис. 1.29).

Этот вектор называется ротором(вихрем) вектораи обозначается символомrot . Таким образом выражение (1.64) можно записать в виде

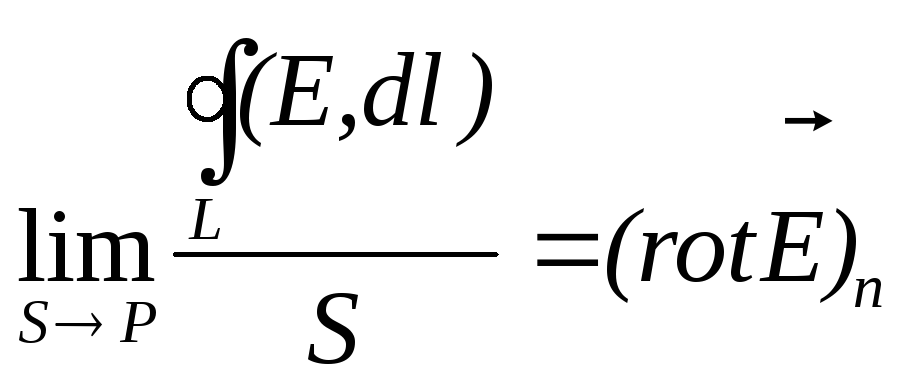. (1.65)

Выберем в плоскости, параллельной координатной плоскости YZ, прямоугольный контурL со сторонамиYиZ(рис. 1.30).

П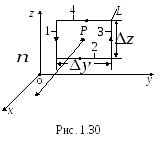ри указанном стрелками направлении обхода положительная нормальк плоскости контура параллельна оси Х. Следовательно, вычислив предел в выражении (1.65), можно найти проекцию ротора на ось Х (rot )_х.

При стягивании площади контура к точке Р, длины отрезковYиZ будут стремиться к нулю, поэтому изменениемЕ_Y на сторонах 2 и 4 контура и изменением Е_Z на сторонах 1 и 3 можно пренебречь. Учтем также, что на стороне 1 контура направление обхода противоположно осиZ, а на стороне 4 оно противоположно осиY. В итоге циркуляция вектора по контуруLопределяется выражением

(1.66)

Представим приращения (Е_Z3-E_Z1) и(Е_Y4-Е_Y2)в виде

и (1.67)

Из (1.66) и (1.67) получим

(1.68)

где S=Y Z – площадь, охватываемая контуром.

Подставив (1.68) в (1.65), находим

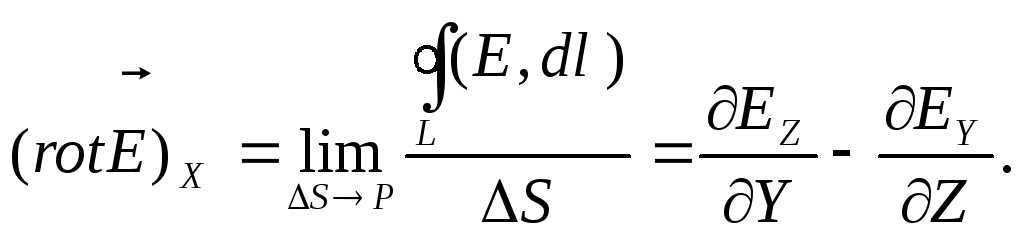(1.69)

Расположив контур в плоскостях, параллельных координатным плоскостям х, уих, zи проведя аналогичные рассуждения, можно для проекций вектораrot на осиу иzполучить выражения:

(1.70)

(1.71)