
- •Часть 1
- •Глава 1
- •1.1. Общие сведения
- •1.2. Расчет настроек регуляторов в одноконтурных аср
- •1.3. Расчет настроек регуляторов в многоконтурных аср
- •1.3.1. Комбинированные аср
- •1.3.2. Каскадные аср
- •1.3.3. Аср с дополнительным импульсом по производной из промежуточной точки
- •1.3.4. Взаимосвязанные системы регулирования
- •1.4. Системы регулирования объектов с запаздыванием и нестационарных объектов
- •1.4.1. Регулирование объектов с запаздыванием
- •1.4.2. Регулирование нестационарных объектов
- •1.5. Предварительный выбор структуры
- •1.6. Оптимальная фильтрация и прогнозирование случайных процессов. Оптимальное оценивание состояния объекта
- •Глава 2
- •2.1. Последовательность выбора системы автоматизации*
- •2.2. Регулирование основных технологических параметров
- •2.3. Регулирование процессов в химических реакторах
- •2.3.2. Регулирование реакторов с перемешивающим устройством
- •2.3.3. Особенности регулирования трубчатых реакторов
- •Часть 2
- •Глава 3
- •Глава 4
- •4.1. Типовые задачи вычисления неизмеряемых величин и обобщенных показателей
- •4.2. Вычисление интегральных и усредненных значений измеряемых величин
- •4.3. Учет и компенсация динамических связей между измеряемыми величинами
- •4.4. Вычисление неизмеряемых величин по уравнениям регрессии (косвенные измерения)
- •4.5. Автоматическая расшифровка хроматограмм
- •4.6. Прогнозирование показателей процесса
- •Глава 5
- •5.1. Формирование критериев оптимальности
- •5.2. Типовые постановки задач оптимального управления технологическими процессами
- •5.3. Декомпозиция и агрегирование оптимизационных задач
- •5.4. Управление технологическими процессами с параллельной структурой
- •5.5. Оптимальное управление системами с последовательной структурой и с рециклами
- •5.6. Способы упрощения решения задач оптимального управления технологическими процессами
- •5.7. Оптимальное управление периодическими процессами
- •5.8. Уточнение модели управляемого объекта по данным текущих измерений
- •Часть 8
- •Глава 6 техническое обеспечение систем управления
- •6.1. Управляющий вычислительный комплекс
- •6.2. Устройства связи с объектом
- •6.3. Устройства связи с оперативным персоналом
- •6.4. Архитектура управляющих вычислительных комплексов
- •6.5. Системы непосредственного цифрового управления
- •Глава 7
- •7.1. Основные понятия
- •7.2. Специальное программное обеспечение асутп
- •7.3. Разработка функционально алгоритмической структуры асутп*
- •8.1. Асутп микробиологического синтеза лизина ' в биореакторах периодического действия
1.6. Оптимальная фильтрация и прогнозирование случайных процессов. Оптимальное оценивание состояния объекта
Один из способов формирования требуемого управляющего воздействия— синтез такой линейной системы (формирующего устройства), реакция которой на заданный входной сигнал совпадает с желаемым сигналом m(t) или мало от него отличается. Способ решения такой задачи позволяет понять существо методов оптимальной фильтрации и прогнозирования стационарных •случайных процессов.
Обозначим импульсную характеристику формирующего устройства w(t). Для физически реализуемой системы эта характеристика удовлетворяет требованию
![]() (1.59)
(1.59)

Рис. 1.56. Расщепление желаемого сигнала m(t) на m+(t) и m-{t)
Первоначально предположим, что сигналом на входе формирующего устройства является б-функция. Тогда его выходом является характеристика w(t); она должна минимизировать-квадр этичное отклонение
![]() (1.60)
(1.60)
Если функция m(t) равна нулю при t<.0, то решение задачи очевидно: w*(t)=m(t).
Если m(t) отлична от нуля при t<C.O, то импульсная характеристика, минимизирующая (1.60), должна быть равна m{t) лишь при f>0 и обращаться в нуль при отрицательных значениях t. На рис. 1.56 показаны такая функция m(t) и оптимальная импульсная характеристика.
Таким образом, во временной области решение задачи очевидно. Несколько сложнее решить ее, если условия заданы в частотной области. Например, задано преобразование па Фурье М(ш) функции m(t) и требуется найти амплитудно-фазовую частотную характеристику W(m) формирующего устройства. Для определения W*{ia>) нужно представить М(т) в виде суммы двух слагаемых:
![]() (1.61>
(1.61>
Первому слагаемому соответствует оригинал m+{t), равный-нулю при отрицательных значениях t, а второму — при положительных. Разложение (1.61) называют расщеплением. Равенство w(t)=m+(t) в частотной области запишется следующим образом:
![]() (1.62)
(1.62)
Если функция М(ш) дробно-рациональная, то разложение (1.61) можно выполнять, не переходя к оригиналам, а воспользовавшись тем, что для функции f(t), равной нулю при t<C0 и стремящейся к нулю при /->-оо, преобразование Лапласа F(p) имеет все полюсы в левой полуплоскости комплексного переменного. Наоборот, функция, равная нулю при />0, имеет преобразование Лапласа с полюсами в правой полуплоскости.
Пример. Пусть
![]()
Преобразование Лапласа получим из преобразования Фурье заменой to на р-
М{р>- (p+i)(p_i) =7+T+"FrT-
В первом из этих слагаемых полюс р°=—1,так что это М+, во втором полюс равен +1, это Af_. Коэффициенты А и В определим, приведя последнее равенство к общему знаменателю и учитывая, что числитель полученного выражения должен равняться р:
Ар + А + Вр — В = р.
Из условий равенства коэффициентов при одинаковых степенях р получим: А+В=\; А—В=0. Отсюда Л = В = 0,5. Таким образом
*Mto)=
2(to+l)
=Г*('Ю>-
Обобщим задачу синтеза формирующего устройства, предполагая, что на его вход подается сигнал g(t) и требуется так подобрать импульсную характеристику w(t), чтобы выход устройства y(t) минимально отличался от желаемого сигнала m{t).
Если g(t)=0 при ^<0, задача сводится к предыдущей, так как при t<ZQ y(t)=0; при ^>0 нужно сформировать y(t) равным m+(t). В частотной области
7* (to) = G (to) W* (to) = М+ (to),
откуда
W* (((о) = М+ (to)/G (гсо).
Если #(£) =5^0 при /,<0, поступим следующим образом. Отбросим условие физической реализуемости и запишем в частотной области условие равенства желаемого сигнала и сигнала на выводе формирующего устройства:
G (to) W (to) = М (to). (1.63)
Преобразуем это равенство к такой форме, чтобы оригинал слагаемого, зависящего от W(ia>), обращался в нуль при /<0. Для этого представим G(ico) в виде
G(to) = G+(to)G-(to).
Здесь первому сомножителю соответствует оригинал, равный нулю при КО, второму — при />0. Такое представление называют факторизацией. Поделим обе части равенства (1.63) на С~(ш). Получим:
G+ (to) W ((со) = М ((co)/G- (to). (1.64)
Согласно условию физической реализуемости, оригинал функции W(ia>) и, следовательно, произведения G+(i<B)W(ico), должен обращаться в нуль при ^<0; при t^O выбором W(i(a) можем добиться равенства функций времени, соответствующих левой и правой частям выражения (1.64). Таким образом, наи-

Рис. 1.57. Схема, иллюстрирующая постановку задачи оптимальной фильтрации
лучшему выбору соответствует условие
![]()
![]()
Оригинал
первого равен нулю при t<CQ,
второго
— при f>0.
Окончательно
получим:
![]()
Таким образом, учет требований физической реализуемости формирующего устройства осуществляют в частотной области с помощью двух операций — факторизации и расщепления. Факторизацию используют для того, чтобы множителем при W(i(u) оказалась функция, которой во временной области соответствует оригинал, равный нулю при t<0. Операция расщепления соответствует во временной области разбиению оригинала на два слагаемых, одно из которых определено для t^O, другое — для t<.0.
Оптимальная фильтрация и прогнозирование случайных процессов. Пусть на вход линейной системы (фильтра) подается случайный сигнал g(t), равный сумме полезного сигнала y(t) и помехи e(t). Для y(t) и e(t) известно, что это случайные стационарные процессы со спектральными плотностями Sy((o) и Se((a). Требуется найти такую характеристику фильтра W(m), чтобы сигнал у (t) на его выходе минимально в среднеквадратичном смысле отличался от желаемого сигнала (рис. 1.57). В свою очередь, желаемый сигнал тем или иным способом связан с полезным сигналом. Если, например, m(t)=y(t), то задача фильтра заключается в выделении сигнала из его смеси с помехой. Если m(t)=dy/dt, фильтр реализует помехоустойчивое дифференцирование y(t). Если m(t)=y(t+x), осуществляется помехоустойчивый прогноз полезного сигнала. В общем случае связь между y(t) и m(t) удобно задать в частотной области в виде
![]()
При этом частотная характеристика оператора связи далеко не
всегда физически реализуема. Для задачи выделения полезного сигнала W9r(ia) — l; для задачи дифференцирования №Эт(ио) =«о; для задачи прогноза W3i(m) =e'MT. Физически реализуема характеристика эталонного оператора только в первом из этих трех примеров.
Критерием оптимальности поставленной задачи является среднеквадратичная величина ошибки е между желаемым сигналом и сигналом у на выходе фильтра. Обозначая для краткости чертой операцию усреднения, запишем:
![]()
В частотной области среднеквадратичная ошибка запишется в форме
![]()
![]()
Условие минимума этого выражения по №(<ш) с учетом того, что ]W(i(o) \2=W(m)W(—ia), а производная dW(—ш)/ /dW(m) =—1, приводят к равенству
(1.65)
![]()
При этом требование физической реализуемости фильтра никак не учитывалось. Произведение Sg(a))W(m) равно, как известно, взаимной спектральной плотности сигналов на входе и выходе фильтра Sgy(m).
Таким образом, амплитудно-фазовую характеристику фильтра без учета физической реализуемости следует выбирать так, чтобы взаимная спектральная плотность сигнала на входе и выходе фильтра была равна взаимной спектральной плотности входного и желаемого сигналов. Для некоррелированных сигнала y(t) и помехи e(t) спектральная плотность входного сигнала
![]()
Взаимная спектральная плотность g(t) и m(t) может быть выражена через характеристику эталонного оператора ^этМ:
![]()
Таким образом, АФХ оптимального фильтра, найденная беа
учета физической реализуемости, имеет'вид:
![]() (1.66)
(1.66)
Если оказывается, что найденная таким образом характеристика реализуема, она дает оптимальное решение. Однако знать эту характеристику полезно и тогда, когда она не реализуема, так как при подстановке ее в 5е (со) вычисленное значение среднеквадратичной ошибки дает тот нижний предел, меньше которого эта ошибка заведомо быть не может.
Перейдем к учету условий физической реализуемости. Аналогично задаче синтеза формирующего устройства преобразуем равенство (1.66) так, чтобы зависящее от W слагаемое имело оригинал, равный нулю при i^<0. Для этого проведем факторизацию Sg(co):
![]()
Оригинал первого сомножителя отличен от нуля при /^0, а второго — при ^<;0. В силу симметрии Sg(co) функции Sg+ и 5Й~ удовлетворяют равенству
![]()
Разделив обе части этого равенства на Sg~, получим:
![]() (1.67)
(1.67)
Левая часть этого равенства для физически реализуемой функции W(m) имеет оригинал, равный нулю при /<0, а при f^tO выбором W можем сформировать нужную функцию. Наилучшему выбору W соответствует совпадение оригиналов от левой и правой частей равенства (1.67) при t^O. После расщепления правой части равенства (1.67).
![]()
![]()
![]() (1.68)
(1.68)
Пример. Решить задачу об оптимальном выделении сигнала у из смеси с помехой е, если спектральные платности Sy и Se имеют вид
![]()
а корреляция полезного сигнала и помехи отсутствует.

Рис. 1.58. Импульсная характеристика физически нереализуемого фильтра
Без учета физической реализуемости фильтра его частотная характеристика примет форму
![]()
Соответствующая импульсная характеристика показана на рис. 1.58. Чтобы учесть физическую реализуемость, проведем факторизацию Sg:
![]()
и расщепление Sgm/Sa-:

Для определения А и В имеем урав!
![]()
Откуда
![]()
Теперь получим
![]()
Обобщение задачи оптимальной фильтрации. Рассмотренная выше задача оптимальной фильтрации была обобщена в самых разных направлениях. Остановимся на одном из таких обобщений, связанным с тем, что ошибка системы для разных частот имеет различный вес. Этот фактор можно учесть, введя в критерий оптимальности весовую функцию, в результате чего он примет вид:
![]() (1.69)
(1.69)
Чем больше весовая функция #(©) на некоторой частоте, тем меньше ордината спектральной плотности ошибки, соответствующая оптимальному решению. Примером критерия, имеюще-
го вид (1.69), служат обобщенные интегральные критерии, где наряду с дисперсией ошибки е учитывается дисперсия ее производных. Так, минимизация выражения
![]()
![]()
Полученную выше формулу для расчета АФХ оптимального фильтра нетрудно распространить на случай функционала (1.69). Для этого нужно записать условие стационарности функционала /я по W. Очевидно, это условие будет отличаться от равенства (1.65) только тем, что левая и правая его части будут содержать в качестве множителя функцию Нш. Получим:
![]()
(1.70)
Для расчета оптимальной физически реализуемой АФХ фильтра проведем, как и выше, факторизацию Sg и Н, после чего поделим левую и правую части равенства (1.70) на произведение Sg~H~. Получим:
![]()
![]() (1.71)
(1.71)
Оптимальнее оценивание состояния объекта. В задаче оптимальной фильтрации предполагались известными спектральные плотности полезного сигнала и помехи, которые могут быть найдены посредством статистической обработки реализаций этих стационарных и эргодических процессов. При этом мы не предполагали известным механизм генерации этих сигналов. Между тем, если полезный сигнал представляет собой вектор-функцию у, характеризующую состояние технологического процесса, то приближенно известна его математическая модель; часть составляющих вектора состояния или некоторые зависящие от него переменные можно измерять и по результатам текущих измерений уточнять оценку у; сигнал, а в некоторых случаях и помехи, нельзя считать стационарными процессами.
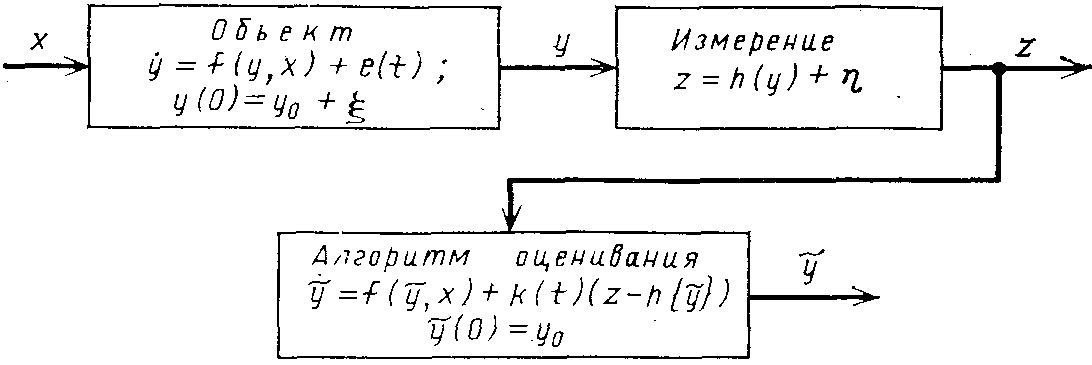
Расчет функции у (t) при таких предположениях называют оцениванием состояния; если же в момент t нужно рассчитать у(/+т), то имеем задачу оценивания с прогнозом состояния. Схема, иллюстрирующая постановку задачи оценивания, приведена на рис. 1.59. Предполагаются известными модель объекта: статистические характеристики сигналов е, | и г\, характеризующие ошибки и случайные возмущения в модели, ошибки при измерении входных воздействий и при измерении переменных состояния соответственно; функция z (t) и вектор Потребуется оценить вектор у в момент t или (t+x). Основы теории оценивания развиты в работах Калмана и Бьюси [23].
Для систем регулирования модель объекта можно линеаризовать. Поэтому рассмотрим синтез алгоритма оценивания для линейных систем. Модель системы в векторно-матричной форме записи имеет вид (1.72), а модель измерений — вид (1.73):
![]() (1.73)
(1.73)
Начальные условия уравнения (1.72) случайны:
![]() (1.74)
(1.74)
В уравнениях (1.72) — (1.74) y(t)—n-мерный вектор состояния; z(t) — /-мерный вектор измеряемых выходов; e(t)—«-мерный вектор случайных возмущений; t\(t)—/-мерный вектор случайных ошибок измерений; g — случайная составляющая начальных условий; А — квадратная матрица (пУ<.п); С — прямоугольная матрица (1Хп).
Требуется по наблюдениям за процессом z(t) найти такую оценку состояния процесса y(t), при которой достигает минимума критерий
 (1.75)
(1.75)
Здесь Т — интервал, в течение которого проводят наблюдения. Первое слагаемое в (1.75) представляет собой квадратичную
форму разности между начальным значением оценки г/(0) и начальным состоянием процесса г/о- Подобные же квадратичные формы, оценивающие погрешность модели и измерений, содержатся в подынтегральном выражении функционала. Матрицы Лг1, i? и Q определяют весовые коэффициенты, оценивающие важность той или иной составляющей ошибки. Пусть e(t), т)(0—случайные процессы типа белого шума, не коррелированные друг с другом и со случайным вектором |, а их средние значения равны нулю. В качестве матрицы Р0 берут матрицу ковариаций случайной помехи £ оценки начального состояния:
![]()
![]() (1.76)
(1.76)
По диагоналям этих матриц стоят корреляционные функции отдельных составляющих процессов e(t) и r\(t),a на остальных местах — взаимнокорреляционные функции двух разных составляющих этих процессов. Элементы ковариационных матриц случайных ошибок отражают неопределенность наших знаний. Чем больше эта неопределенность, тем с меньшим весом входит соответствующее слагаемое в критерий I.
Для решения задачи о минимуме / удобно ввести новую переменную
![]() (1.77)
(1.77)
и переписать критерий / в форме
 (1.78)
(1.78)
При этом необходимо учесть связь (1.77) между у я и:
![]() (1.79)
(1.79)
Функцию z(t) можно наблюдать; минимум ищется по у(0) иг/. Поставленная задача выпукла, поэтому ее решение существует и является единственным. В соответствии с процедурой принци-
па максимума [40] запишем для задачи (1.78), (1.79) функцию Гамильтона
![]()
![]() (1.80)
(1.80)
Уравнения для сопряженных переменных
![]()
![]() (1.81)
(1.81)
Краевые условия для уравнения (1.81)—нулевые: г|з(7')=0. Начальное значение i|)(0) определяется [53] в виде
![]() (1.82)
(1.82)
откуда
![]() (1.83)
(1.83)
Подставляя (1.80) в уравнение (1.79), получим:
![]() (1.84)
(1.84)
Таким образом, для вычисления оптимальной оценки y*(t) состояния процесса необходимо решить совместно уравнения (1.81) и (1.84), причем для уравнения (1.81) заданы условия в конце интервала наблюдения при t = T, а для уравнения (1.84) начальные условия определены через г|)(0). Так как граничные условия для у и г|) заданы на разных концах интервала наблюдения, то одно из уравнений нужно решать в прямом времени, а другое — в обратном. Однако поскольку у входит в правую часть уравнений (1.81), а ^ — в правую часть уравнений (1.84), подобная процедура затруднена. Чтобы «развязать» систему (1.81), (1.84), удобно перейти к вспомогательным переменным Ъ и ввести вспомогательную матрицу Р, так что
![]()
(1.85)
Подставляя это выражение в (1.84), получим:
![]() (1.86)
(1.86)
С учетом (1.81) имеем:
![]() (1.87)
(1.87)
Подберем теперь вспомогательную матрицу Р так, чтобы в (1.87) сумма слагаемых, содержащих ty, обратилась в нуль. Эта сумма равна
![]()
Условие ее равенства нулю приводит к дифференциальному уравнению для матрицы Р:
(1.88>
![]()
Если матрица Р удовлетворяет уравнению (1.88), то из равенства (1.87) вытекает уравнение для расчета вектора b(t):
![]()
(1.89)
Начальные условия для уравнений (1.88), (1.89) следует из начальных условий (1.82) для ib. Действительно, требование
![]()
окажется выполненным, если
(1.90)
![]()
Уравнения (1.88) и (1.89) не содержат в правых частях никаких других переменных, кроме Р, Ь и наблюдаемого вектора г. Они могут быть проинтегрированы в прямом времеви от £=0 до t=T. Это позволяет выразить ty(t) через y(t) в соответствии с (1.85), найти y{T)=b{t) и переписать уравнение (1.86)ввиде
![]()
Решение этого уравнения в обратном времени определит искомую оценку у (t).
Однако полученная оценка может быть найдена лишь для тех моментов t, которые лежат внутри интервала наблюдения (О, Т). Часто требуется оценить вектор состояния в момент Т или даже прогнозировать его значение на х вперед. В первом случае оценка вытекает непосредственно из условия яр (7") = О, т. е. y(t) (где t — текущий момент времени, совпадающий с концом интервала наблюдения) получается из решения уравнения (1.89.) заменой в нем b(t) на y(t):
![]()
(1.91)
Здесь матрица Р определяется уравнением (1.88).
Прогнозирующую оценку у (t+x) получают из уравнения (1.91) интегрированием его до момента t+x. При этом начиная с момента t до t+x матрицу Q(t), определяющую веса погрешностей измерения, полагают равной нулю (измерения отсутствуют, их неопределенность сколь угодно велика), т. е. на участке

от / до t+x уравнение (1.91) упрощается и принимает вид: у= =Ау. Аналогично на интервале {t, t+x) упрощается уравнение (1.88) для подсчета элементов матрицы Р.
Пример {43]. Процесс в проточном химическом реакторе с непрерывным
перемешиванием характеризуется системой дифференциальных уравнений

![]()
![]()
Аналогичные предположения сделаем о случайной функции r\(t) и векторе 1о:
![]()
Здесь![]()
Уравнение для оценки вектора y(t) по результатам текущих измерений на интервале (0,0 примет вид уравнения (1.89), в котором p(t)=b(t):

Элементы матрицы Р вычисляются согласно уравнению (1.88):

На рис. 1.60 показаны изменения во времени элементов матрицы Р, а также оценки вектора концентраций у в системе для следующих исходных, данных:

дисперсия погрешностей измерения Q~' = 0,05.
