Вольников / КНИГИ / Дудников / Фильтрация с 124

Часть 2

МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ СИСТЕМ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ ■

ГЛАВА 3

АЛГОРИТМЫ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ В АСУТП

3.1. ЗАДАЧИ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ

Основным видом информации о состоянии объекта управления в АСУТП являются текущие значения технологических парамет­ров, которые преобразуются автоматическими измерительными устройствами в сигналы измерительной информации. После приведения к стандартной форме эти сигналы вводятся в УВМ и представляют в ней значения соответствующих параметров в определенный момент времени.

Однако формируемый таким образом массив исходной ин­формации' не пригоден для непосредственного использования при решении задач управления, так как требуется его предвари­тельная обработка, которую принято называть первичной*. Для того чтобы сформулировать задачи первичной обработки инфор­мации (ПОИ) в АСУТП, необходимо рассмотреть последова­тельность преобразований, которым подвергается измеряемая величина в типовом информационно-измерительном канале (ИИК), схема которого представлена на рис. 3.1**.

Измеряемая величина x(t), которую обычно считают стацио­нарной случайной функцией времени, воздействует на вход из­мерительного преобразователя (ИП), на выходе которого форми­руется сигнал измерительной информации у(t). Принцип дейст­вия большинства ИП таков, что их выходной сигнал зависит не только от значения измеряемой величины, но и от ряда других величин Zj, которые называют влияющими.

Например, термоэлектрический преобразователь температу­ры (ТПТ) преобразует измеряемую величину — температуру — в сигнал измерительной информации — э.д.с. Однако этот сигнал зависит не только от измеряемой температуры, которая воспри-

* В отличие от вторичной переработки, которой исходная информация подвергается в алгоритмах контроля и управления.

** В состав ИИК входит также модуль нормализации, который на рис. 3.1 не показан, так как не требует решения дополнительных задач ПОИ.

•нимается рабочим спаем, но и от температуры свободных спаев, которая в данном случае является влияющей величиной.

В общем случае без учета динамической характеристики ИП связь между сигналами на его входе и выходе описывается ста­тической характеристикой вида:

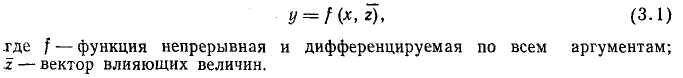
Например, статическая характеристика ТПТ в первом при­ближении может быть описана линейной функцией

где у — э. д. с. ТПТ, мВ; х — температура рабочего спая, °С; z — температу­ра свободных спаев, °С; k — коэффициент, численное значение которого за­висит от материала электродов ТПТ (например, для хромель-копелевого ТПТ £=0,0695 мВ/°С).

Однозначное соответствие между сигналом измерительной информации и измеряемой величиной соблюдается только при постоянных значениях влияющих величин. Для каждого ИП эти номинальные значения z°/ указывают в его паспорте. Подставив их в уравнение (3.1), получим номинальную (паспортную) ста­тическую характеристику ИП:

В большинстве случаев для ТПТ номинальное значение тем­пературы свободных спаев принято равным 0°С, поэтому пас­портная статическая характеристика, полученная из (3.1а) при z = 0, имеет вид: y = kx.

Будем считать, что в процессе работы ИП значения влияю­щих величин соответствуют номинальным; следовательно, пре­образование значений измеряемой величины в сигнал измери­тельной информации выполняется в соответствии с паспортной статической характеристикой (3.2). Казалось бы, это должно гарантировать точное преобразование х в у, однако и при вы­полнении этого условия всякий реальный ИП вносит в резуль­таты некоторую погрешность. На структурной схеме (см. рис. 3.1) она представлена в виде случайной функции времени e(t), которая накладывается на полезный сигнал y(t) измери­тельной информации. Помеха e(t) моделирует не только случайную погрешность Ни, но и электрические наводки в соедини­тельных проводах, вызванные магнитными полями электросило­вого оборудования; влияние пульсаций давления и расхода в технологических трубопроводах вследствие работы насосов и компрессоров и другие факторы. На вход УВМ поступает сум-мяпньтй сигнал:

Поскольку АСУТП имеет много ИИК, их обслуживание раз­делено во времени, каждый канал периодически с периодом to подключается на короткое время ко входу УВМ. В результате непрерывная функция g(t) преобразуется в последовательность импульсов, модулированных по амплитуде функцией g(t). На структурной схеме ИИК (см. рис. 3.1) функцию квантования сигнала g(t) по времени выполняет коммутатор, условно изобра­женный в виде ключа, замыкаемого с периодом t₀. На выходе коммутатора образуется решетчатая функция:

Следующим видом преобразования, которому подвергается сигнал измерительной информации в ИИК, является квантова­ние по уровню, выполняемое аналого-цифровым преобразовате­лем (АЦП). При этом амплитуды импульсов g{jt₀) преобразу­ются в числа g*(jt₀), выраженные в коде, с которыми в даль­нейшем оперирует ЦВМ. Современные управляющие вычисли­тельные машины, как правило, используют двоичный код и опе­рируют с числами, имеющими 8 или 16 разрядов. Операция квантования дискретной величины g(jt₀) по уровню описывается следующим выражением:

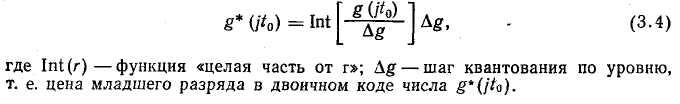
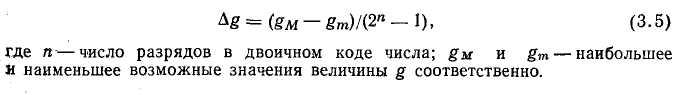
Величина Ag определяется из условия:

Число g*(jto), полученное в результате выполнения всех пре­образований измеряемой величины в ИИК, вводится в одну из ячеек запоминающего устройства УВМ и в дальнейшем пред­ставляет в машине значение измеряемой величины x(t) в мо­мент времени t = jt₀.

Из изложенного вытекают следующие основные задачи пер­вичной обработки информации в АСУТП:

1) фильтрация сигнала измерительной информации от слу­чайной помехи (погрешности) e(t);

2. восстановление значения измеряемой величины x(t) по сигналу измерительной информации y(t);

3. коррекция восстановленных значений измеряемой величины с учетом отклонения условий измерения от номинальных;

4. восстановление значений измеряемой величины x(t) приjto<t<. (/+l)^o, т. е. интерполяция и экстраполяция.

Кроме того, необходимо оценить влияние квантования сиг­нала измерительной информации по времени и по уровню на точность его представления, а также рассмотреть методы конт­роля и повышения достоверности исходной информации в АСУТП.

3.2. ВЫБОР РАЗРЯДНОСТИ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ

В УВМ И ЧАСТОТЫ ОПРОСА ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ.

ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ СИГНАЛА

В современных УВМ наибольшее распространение получил ре­жим обработки данных с фиксированной запятой [48]. При этом погрешность представления исходной информации, вызванная квантованием по уровню, не превышает по абсолютной величине единицы младшего разряда, определяемой соотношением (3.5). Если задана допустимая относительная погрешность квантова­ния по уровню б_к, то необходимое число разрядов определяется из условия

Обычно я>8, так что относительная погрешность квантования по уровню не превышает 0,4%, т. е. является пренебрежимо ма­лой по сравнению с погрешностью измерительного преобразова­теля.

При разработке АСУТП важен выбор периода ^о квантова­ния по времени сигналов измерительной информации. Эта зада­ча решается с учетом двух противоречивых соображений. С од­ной стороны, увеличение периода t₀ снижает загрузку УВМ опе­рациями сбора и первичной обработки исходной информации. В результате большая доля вычислительных ресурсов системы может быть использована на решение задач контроля и управ­ления более высокого уровня. Это соображение особенно важно для микропроцессорных АСУТП. С другой стороны, при увели­чении периода to возрастает погрешность определения действи­тельного значения измеряемой величины y(t) по решетчатой функции g*(jto). Эта погрешность проявляется при восстановле-

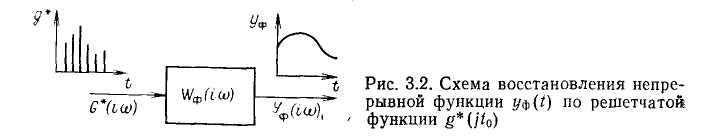
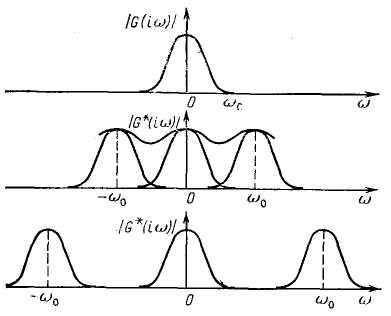
Рис. 3.3. Спектры функций:

а — непрерывной; б, в — решетчатой при Шо<2о)_с и при (йо>2ю_с

нии значений функции у (t) в моменты времени, не совпадающие с момен­тами отсчета tj = jt₀.

Задачи восстановления непрерывной функции по ее дискретным значениям делятся на задачи экстра­поляции и интерполяции. Экстраполяцией называ­ют определение будущих

значений функции с момента очередного отсчета до момента по­ступления следующего отсчета. Интерполяцией называют опре­деление промежуточных значений функции между двумя полу­ченными отсчетами.

В общем случае восстановление непрерывного сигнала по решетчатой функции производится формирующим фильтром, представляющим собой линейное динамическое звено с ампли­тудно-фазовой характеристикой (АФХ) №_ф(ко) (рис. 3.2). Сле­довательно, для восстановленного сигнала справедливо следую­щее соотношение:

где G*(ico)—преобразование Фурье функции g*(/'o).

Из теории импульсных систем известно [55], что спектр ре­шетчатой функции является периодической функцией с перио­дом, равным частоте квантования (uo = 2njt₀.

Смещенные компоненты спектра могут частично перекрывать друг друга, причем степень перекрытия увеличивается по мере уменьшения частоты ©₀, т. е. при увеличении периода квантова­ния t₀ (рис. 3.3). В результате наложения спектр решетчатой функции" искажается, и из него невозможно выделить спектр ис­ходной непрерывной функции. Исключение составляет физически нереализуемый случай, когда спектр непрерывной функции огра­ничен, т. е.

а частота квантования удовлетворяет условию

При этом смещенные компоненты в спектре решетчатой функ­ции g(jto) не перекрываются, и из него можно выделить главную несмещенную составляющую, совпадающую со спектром непре­рывной функции g(t) (см. рис. 3.3). Для точного восстановления исходной непрерывной функции по решетчатой функции необхо-

димо использовать идеальный нереализуемый фильтр с АФХ

Действительно, погрешность восстановления, очевидно, равна

или в преобразованном по Фурье виде¹—

Для идеального фильтра (3.7) при выполнении условия (3.6) справедливо равенство

и, следовательно

Соотношение (3.6) составляет содержание теоремы Котель-никова — Шеннона, которая определяет необходимые условия передачи без искажения информации, содержащейся в непрерыв­ном сигнале при его квантовании по времени и последующем восстановлении.

Если для восстановления используют фильтр с АФХ W$(iai), отличающейся от (3.7), то даже при выполнении условия (3.6) точное восстановление исходной непрерывной функции невоз­можно. Погрешность восстановления получим, применив обрат­ное преобразование Фурье к выражению (3.8) с учетом (3.9):

Таким образом, погрешность восстановления зависит от свойств исходной функции g(t), периода квантования t₀ [эти два фактора определяют G*(tco)] и АФХ формирующего фильтра

Рассмотрим наиболее распространенные методы экстраполя­ции и интерполяции.

Метод ступенчатой экстраполяции (экстраполятор нулевого порядка) состоит в том, что значение восстанавливаемой функ­ции г/ф(/) для любого момента времени jt_o<t<i (j-\-l)t_Q прини­мают равным g*(jt₀) рис. 3.4):

Сигнал, восстановленный по алгоритму (3.11), можно, оче­видно рассматривать как сумму двух направленных в разные стороны скачков с амплитудой g*(jt₀), один из которых сдвинут по времени на to:

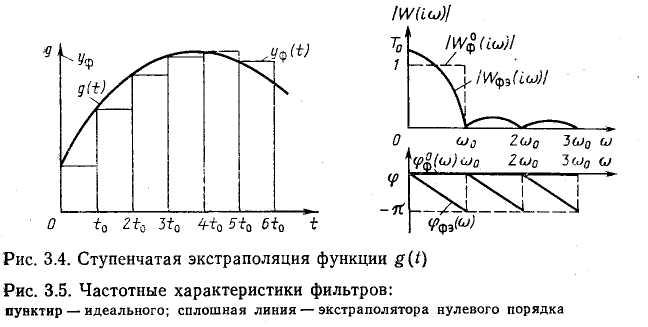
Следовательно, А.ФХ экстраполятора нулевого порядка равна:

Это выражение можно преобразовать, используя тригонометрическую форму комплексного числа

а тригонометрические функции кратных углов:

Подставляя полученное выражение в (3.12) и учитывая, что

получим

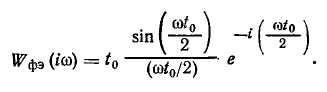
Погрешность экстраполяции обусловлена различием ампли­тудно-фазовых характеристик идеального фильтра (3.7) и экс­траполятора нулевого порядка (рис. 3.5). Для расчета погреш­ности ступенчатой экстраполяции из частотной области удобно перейти к рассмотрению сигналов y$(t) и g(t) (см. рис. 3.4). Погрешность экстраполяции, очевидно, равна

Перейдем в этом выражении к новой переменной x=t—jt₀, которая может изменяться в пределах от 0 до t₀; тогда (3.13) можно записать в виде: e₃(t) =g"(0)—g(x).

Если g(t) является стационарной случайной функцией, то математическое ожидание погрешности e₃(t) при усреднении по множеству интервалов x,- = t—jt₀, / = 0,1,2... равно нулю, так как

в силу линейности операции определения математического ожи­дания

Дисперсия погрешности экстраполяции равна: наибольшего значения при _т—_yt₀. Усредняя D_e{%) по т. в пределах от 0 до t₀, окончательно получим:

формулы (3.14) следует, что' дисперсия погрешности экс­траполяции зависит от т и

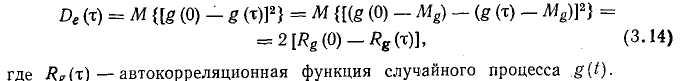
Из достигает где М — знак математического ожидания.

Это выражение позволяет рассчитать дисперсию погрешно­сти экстраполяции по заданному периоду квантования t₀ и авто­корреляционной функции R_g. Его же можно использовать для определения периода квантования t₀, если задано наибольшее допустимое значение среднеквадратичной погрешности экстра­поляции о_е* и известна автокорреляционная функция R_g(x). Для этого удобно использовать графо-аналитический метод (рис. 3.6).

По графику функции R_e(t) определяют такое значение i = t₀, при котором удвоенная средняя высота заштрихованной фигуры ABC (т. е. удвоенный отрезок ДЕ) будет равна задан­ному значению (a_e*)²=D_e. Если ИИК содержит звено чистого запаздывания т₀ (например, ввиду необходимости транспортиро-

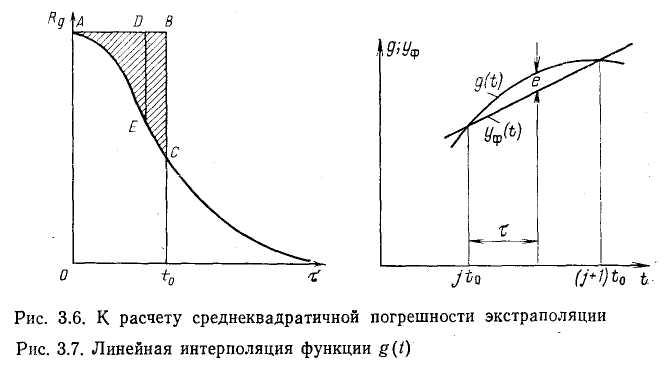
вания пробы от технологического потока до чувствительного эле­мента ИП),,то для расчета среднеквадратичной погрешности экстраполяции можно использовать формулу (3.15) с заменой в ней пределов интегрирования: нижнего на то, а верхнего — на

('о+то). Наряду с ИП непрерывного действия в АСУТП применяют и датчики дискретного действия, например хроматографы. Они осуществляют квантование по времени измеряемой величины с собственным периодом t_g, который обычно значительно выше •периода опроса t₀. В этом случае результирующий период кван­тования по времени в данном ИИК определяется из условия'

Для оценки погрешности экстраполяции можно использовать выражение (3.15) с заменой в нем ^о на i_g.

Линейная интерполяция (рис. 3.7) является простейшим ме­тодом интерполяции, в основе которого лежит кусочно-линейная аппроксимация функции g(t) на интервале значений jto<-t<£

<(/+1)*о.

Уравнение прямой, проходящей через точки g(jto) и ё{(/+1)^о]. можно записать в виде:

Погрешность линейной интерполяции

Подставляя в это выражение значение г/ф(О из формулы (3.16), возводя его в квадрат и усредняя по множеству интервалов, а затем по т в пределах от 0 до to, получаем выражение для дис­персии погрешности линейной интерполяции:

В литературе описаны и другие, более сложные методы ин­терполяции и экстраполяции [24], однако на практике их при­меняют редко. Современные УВМ обеспечивают достаточно вы­сокую частоту опроса ИИК, поэтому обычно удается обеспе­чить требуемую точность восстановления измеряемых величин, используя простейший метод ступенчатой экстраполяции. Обыч­но среди десятков и даже сотен ИИК можно выделить несколь­ко групп параметров, близких по частотным спектрам. Тогда можно выбрать общий период опроса для каждой группы дат­чиков. Например, в производстве разбавленной азотной кислоты опрос группы датчиков, контролирующих малоинерционный про­цесс контактного окисления аммиака, проводится с периодом 15 с, а опрос датчиков на инерционном процессе абсорбции — с периодом 2 мин.

Выбор частоты опроса измерительных преобразователей через число нулей случайного процесса. Выбор частоты опроса t₀ по формуле (3.15) требует знания корреляционной функции R_s(r) случайного процесса g(t). Для получения оценки корреляцион­ной функции необходим значительный объем вычислений. Кро­ме того, часто проще и естественнее задать не дисперсию ошиб­ки Д» от замены непрерывного случайного процесса ступенча­тым, а отношение этой величины к дисперсии случайного про­цесса D. Учтем также важность гарантии того, что выбранная частота опроса не приведет к появлению большей относитель­ной погрешности, чем заданное значение, т. е. важно получить оценку сверху для периода опроса t₀.

Для решения поставленной задачи воспользуемся неравен­ством [22]:

Если бы продолжительность корреляционной функции можно было оценить без построения этой функции, то неравенство (3.17) позволило бы оценить интервал опроса /₀- Ниже получим оцен­ку величины А через среднее число нулей случайного процесса No, т. е. через среднее число пересечений им линии своего ма­тематического ожидания в единицу времени. Предварительно отметим, что рассмотрение процессов с корреляционной функ­цией конечной продолжительности более естественны, чем про­цессов со спектральной плотностью, ограниченной частотой среза, так как первые, в отличие от вторых, физически реали­зуемы.

Известна связь среднего числа нулей N_o со спектральной плотностью случайного процесса 5(ш):

Пользуясь этой формулой, попытаемся найти минимальную продолжительность корреляционной функции R_g, имеющей за­данное число нулей N_o. В силу свойств преобразования Фурье, произведение любых двух функционалов, однозначнскопределяе-мых корреляционной функцией R_g, один из которых имеет раз­мерность времени, а другой — частоты [последний выражается через преобразование Фурье от R_g(r)], не изменяется при сжа­тии или растяжении корреляционной функции, т. е. при измене­нии масштаба времени.

Анализ размерности правой части формулы для iV₀² показы­вает, что среднее число нулей имеет размерность частоты. В ка­честве функционала, имеющего размерность времени, примем

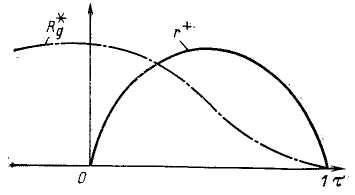
Рис. 3.8. Определение корреляци­онной функции минимальной про­должительности

продолжительность А кор­реляционной функции R_g (t). Таким образом, произведе­ние C=NqA зависит от фор-

мы R_g(x) и не зависит от выбора масштаба времени. Поэтому первоначально зафиксируем /А=1 и при этом условии будем-искать минимум N_o, а точнее JV₀². Чтобы учесть требование ко­нечной продолжительности корреляционной функции, перейдем во временную область. Представим 5(ю) в виде |s(«o) |², что соответствует представлению Rg(x) как свертки двух функций — г⁺(х) и /"(т), первая из которых определена на интервале (О, 1), а вторая — на интервале (0, —1). Формула для среднега числа нулей может быть теперь переписана в виде

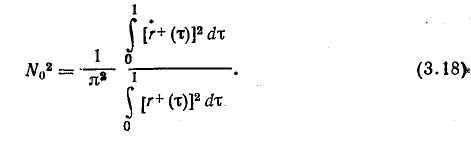
Чтобы найти минимум N\ потребуем, как обычно, минимума числителя при фиксированном значении знаменателя. Задача

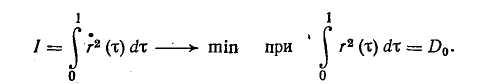
(индекс «+» для краткости записи опущен) решается с испольг-зованием уравнения Эйлера. Составим функционал Лагранжа

и запишем для него уравнение Эйлера

Его решение (а точнее — множество решений):

Подставив решение в условие для заданной дисперсии, получим-A²_Q=D₀/n.

Величина / на найденных решениях /=£>₀&²я²; тогда I/D₀=kn². Это отношение минимально для k = l. Соответствующее решение

т+(т) показано на рис. 3.8. Там же нанесена корреляционная функция R_g*(x), имеющая при заданном среднем числе нулей минимальную продолжительность.

При Д=1 величина С_тщ оказывается равной единице. Следо­вательно, если фиксировано среднее число нулей No, то мини­мальная продолжительность корреляционной функции Amm=l/Af₀.

Пример. Пусть относительная дисперсия, связанная с дискретностью опроса датчиков, не должна превышать пяти процентов. По формуле (3.19) имеем для t₀ оценку

Возвращаясь к неравенству (3.17) и подставляя вместо Д значение Amm, получим оценку сверху для интервала опроса:

Для получения N_o определяют среднее значение случайного процесса, выбирают реализацию такой длины, чтобы случайный процесс пересекал линию среднего значения приблизительно 100 раз, и подсчитывают отношение числа пересечений к длине реализации: No=N(T)/T.

Если число пересечений в точности равно 100, то, обозначив соответст­вующую продолжительность реализации через Г_1Оо, получим:

Таким образом, на реализации длиной Тюо нужно 500 раз отобрать по­казания измерительного преобразователя.

3.3. ФИЛЬТРАЦИЯ ИЗМЕРЯЕМЫХ ВЕЛИЧИН ОТ ПОМЕХ

Фильтрацией называют операцию выделения полезного сигнала измерительной информации y(t) из его суммы с помехой e(t) (см. рис. 3.1). Обычно методы фильтрации основаны на разли­чии частотных спектров функций y(t) и e(t): как правило, поме­ха бывает более высокочастотной. Для выполнения дальнейших выкладок примем следующие допущения:

1) функция y(t) является стационарным случайным процес­сом с известными статистическими характеристиками — матема­тическим ожиданием М_у, дисперсией D_y и автокорреляционной функцией, описываемой следующим выражением:

2) помеха e(t) также является стационарным случайным процессом, некоррелированным с полезным сигналом y(t); для нее известны статистические характеристики М_е = 0, D_e = kD_y:

В результате фильтрации получают оценку г/_ф (г) сигнала из­мерительной информации, к которой предъявляют следующие требования:

она должна быть несмещенной, т. е. должна удовлетворять условию

среднеквадратичная погрешность оценки должна быть мини­мальна, т. е.

Оценку уф(t) будем рассматривать как выходной сигнал ли­нейного динамического звена — фильтра с АФХ №ф(т), на вход которого поступает выходной сигнал ИИК g(t) =y(t)-{-e(t).

В разд. 1.5 сформулирована общая задача синтеза линейно­го оптимального фильтра и получены выражения для АФХ иде­ального (нереализуемого) и физически реализуемого фильтров. Однако синтез оптимального реализуемого фильтра является сложной задачей и, кроме того, требует достаточно точного за­дания характеристик полезного сигнала и помехи. Поэтому на практике обычно ограничиваются так называемым параметри­ческим синтезом фильтров, т. е. задают структуру функции Т^Ф^'со), а ее параметры определяют из условий (3.22) и (3.23).

Спектральную плотность функции e$(t) рассчитывают по формуле

Расчет дисперсии погрешности фильтрации обычно выпол­няют в частотной области, используя выражение

Функции S_e(co) и S_y (ю) являются спектральными плотностями сигналов e(t) и у (t), которые получают в результате преобразо­вания по Фурье автокорреляционных функций (3.20) и (3.21):

На практике применяют несколько простых алгоритмов филь­трации, рассмотренных ниже. Следует отметить, что в АСУТП некоторые методы фильтрации могут осуществляться как аппа-ратурно (с использованием специальных аналоговых устройств), так и программно. Поэтому для каждого такого метода фильт­рации изложен аналоговый и дискретный варианты реализации. Экспоненциальный фильтр*. В аналоговом варианте экспонен-