4.2. Вычисление интегральных и усредненных значений измеряемых величин

При вычислении интеграла (4.1) чаще всего используют мето­ды прямоугольников и трапеций.

Метод прямоугольников (рис. 4.1) основан на аппроксима­ции непрерывной функции х(t) кусочно-постоянной функцией, как при использовании экстраполятора нулевого порядка (см. разд. 3.2). При этом

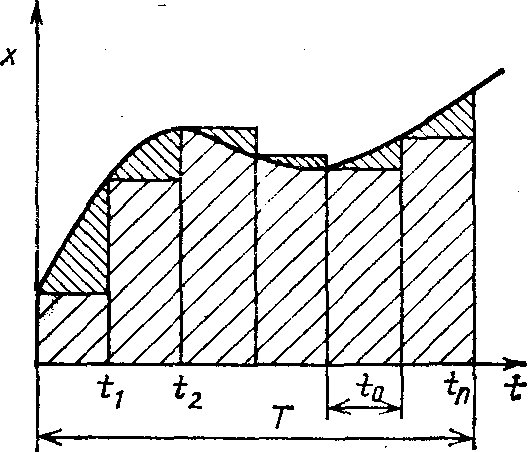
Рис. 4.1. Дискретное интегрирование Рис. 4.2. Дискретное интегрирование

по методу прямоугольников по методу трапеций

оценку величины S_x (Т) с учетом погрешностей измерения определяют по формуле

, (4.4)

где

; (4.5)

x_j=x(jt₀) — значение параметра x в момент t_j=jt₀, ; x_j - погреш­ность измерения параметра х в момент t_j; n=T/t₀ - число периодов отсчета величины х(t) на отрезке времени интегрирования Т.

Рекуррентная формула для вычисления оценки в темпе с поступлением отсчетов, имеет вид:

(j)= (j-1)+ t₀ , 0 jn-1, (0)=0. (4.6)

Погрешность оценки DS_п равна разности между результатами расчета S_x (Т) формулам (4.4) с учетом (4.5) и (4.1):

DS_п . (4.7)

В правой части полученного выражения можно выделить ин­струментальную составляющую DS_пи, зависящую только от по­грешностей измерения x_j:

. (4.8)

Остаток правой части выражения (4.7) описывает методиче­скую составляющую DS_пм погрешности оценки DS_п, определяе­мую численным методом интегрирования и называемую методи­ческой погрешностью:

DS_пм . (4.9)

Среднюю квадратичную погрешность оценки DS_п получают возведением в квадрат и усреднением выражения (4.7). С уче­том (4.9) получают

(4.10)

Первое слагаемое в правой части уравнения (4.10) есть средний квадрат инструментальной составляющей погрешности оценки. В силу линейности операций суммирования и вычисления математического ожидания их можно поменять местами. Тогда

, (4.11)

где R_x(t) - автокорреляционная функция погрешности измерения.

Формула (4.11) упрощается, если погрешность измерения не изменяется в пределах интервала времени интегрирования Т, т. е. если x_j=x_k при любых j и k от 0 до (п—1). В этом случае

, (4.12)

где _x - средняя квадратичная погрешность измерения.

Кроме того, если автокорреляционная функция погрешности измерения затухает за время t₀, т. е. R_x(t)=0 при tt₀, то

В этом случае

. (4.13)

Второе слагаемое в правой части выражения (4.10) равно нулю, так как погрешности измерений x_j, можно считать не­зависимыми от значений х_j, т. е. инструментальная и методиче­ская составляющие погрешности оценки не коррелированы.

Последний член в правой части выражения (4.10) описы­вает средний квадрат методической погрешности ²_пм дискрет­ного интегрирования по методу прямоугольников. Формула для расчета ²_пм, полученная возведением в квадрат и последую­щим усреднением 'правой части (4.9), имеет вид [34]:

²_пм , (4.14)

где R_x() - автокорреляционная функция процесса х(t).

Если период опроса t₀ превышает время затухания автокорре­ляционной функции R_x(), т. е. R_x( )0 при   t₀, то форму­ла (4.14) упрощается:

s²_пм. (4.14а)

Метод трапеции (рис. 4.2) основан на аппроксимации не­прерывной функции х(t) кусочно-линейной функцией, как в методе линейной интерполяции (см. разд. 3.2). Оценку вели­чины S(Т) по этому методу рассчитывают по формуле:

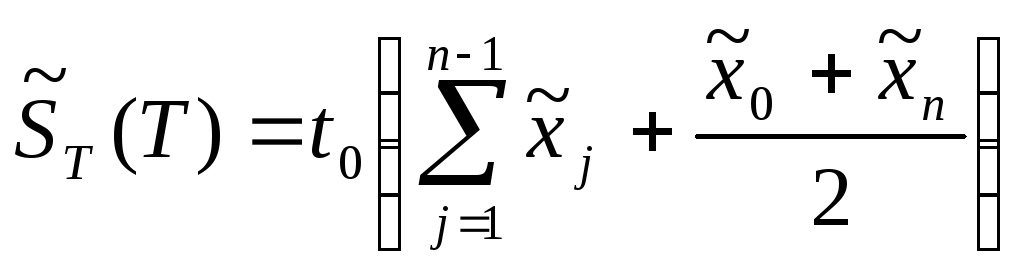. (4.15)

В рекуррентной форме алгоритм вычисления оценки в темпе с поступлением измеренных значенийописывается формулой

1 jn; =0. (4.16)

Формулу погрешности оценки DS_T получают аналогично фор­муле (4.7), как разность правых частей (4.15) и (4.1) с учетом (4.5). Ее можно представить в виде:

DS_T =DS_ТИ+DS_ТМ (4.17)

где DS_ТИ - инструментальная составляющая погрешности, которая совпадает а (4.8); DS_ТМ - методическая составляющая погрешности DS_T, которая опи­сывается выражением

DS_ТМ . (4.18)

Среднюю квадратичную методическую погрешность дис­кретного интегрирования по методу трапеций s²_пм получают возведением в квадрат и последующим усреднением правой части (4.18). Сопоставление полученного при этом выражения с формулой (4.14) показывает, что методическая погрешность при использовании метода трапеций уменьшается по сравнению с полученной методом прямоугольников на величину

s²_м=s²_пм - s²_тм=. (4.19)

В большинстве случаев R_x(Т)=0. Поэтому

s²_м (4.19 а)

Как показывают расчеты [24], заметное (примерно на 10%) уменьшение погрешности дискретного интегрирования при пе­реходе от метода прямоугольников к методу трапеций проис­ходит только при n10, когда существенное влияние на ре­зультат расчета оказывают крайние члены выборки измеренной величины (первый и последний). Поэтому на практике в боль­шинстве случаев применяют метод прямоугольников как более простой и экономичный.

Расчет среднего значения измеряемого параметра х(t) на заданном интервале 0 t T, как следует из формулы (4.2), сводится к вычислению интегрального значения S_x(Т), для че­го может быть использован любой из описанных выше методов дискретного интегрирования. При этом остаются справедливыми все расчетные соотношения, только в формулы (4.11)— (4.14) и (4.19) для вычисления средних квадратических по­грешностей необходимо ввести дополнительный множитель (nt₀)^-2.

При оперативном управлении часто используют средние значения технологических параметров, определяемые на сколь­зящем интервале времени t_j-T t t_j. В принципе для этого также могут быть использованы рассмотренные ранее алгорит­мы дискретного интегрирования, однако для их применения необходимо хранить в оперативной памяти УВМ число п=Т/t₀ значений измеряемой величины. Поэтому для скользящего усреднения часто применяют алгоритм экспоненциального сглаживания (3.33), очень экономичный, однако существенно увеличивающий погрешность оценки скользящего среднего.

Методическая погрешность оценки скользящего среднего равна разности между значениями, вычисленными по фор­мулам (3.33) и (4.2). Первую из них можно преобразовать к виду

. (4.20)

Тогда искомая погрешность

. (4.21)

Средний квадрат методической погрешности оценки скользящего среднего по формуле (4.20) получают возведе­нием в квадрат и усреднением правой части (4.21), что дает [24]:

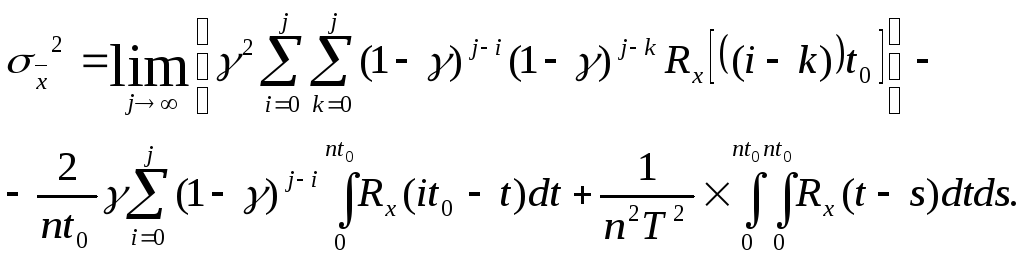(4.22)

Оптимальное значение параметра алгоритма ^* определяют из необходимого условия минимума методической погрешности .

Практически это уравнение можно решить только численно, с помощью ЭВМ.

Расчеты по формуле (4.22), выполненные для автокорреля­ционной функции простейшего вида (3.20) при разных значе­ниях коэффициента , а также разных t₀ и Т, показали [24], что метод экспоненциального сглаживания увеличивает сред­нюю квадратичную методическую погрешность определения текущего среднего в 1,5—3 раза по сравнению с полученной методом прямоугольников. Например, если =1 ч, t₀ =2 мин и T=1 ч, то *=0,14 и =0,04.