Unlock-Линейная алгебра Сикорская 1

Числа a11, a22 , a12 , a21 называются элементами определителя матрицы

второго порядка. Каждый элемент определителя обозначается буквой a с двумя индексами: первый обозначает номер строки, второй – номер столбца, на пересечении которых находится соответствующий элемент (например, элемент a21 – элемент определителя, находящийся на пересечении второй строки и

первого столбца).

Определитель матрицы называют также детерминантом. Для

Заметим также, что числители (4.25) есть определители, полученные из определителя (4.24) путем замены первого столбца (при нахождении x1 ) или

второго столбца (при нахождении x2 ) столбцом из свободных членов. С учетом следующих обозначений

методом исключения неизвестных мы можем найти выражения для x1 , x2 и x3 .

83

Предоставляем читателю выполнить эту процедуру самостоятельно, мы же отметим, что, как и в случае с системой (4.21) решение системы (4.27) представляются в виде дробей с одним и тем же знаменателем, числители же так же как и в первом случае напоминают структуру знаменателя. При этом, число записанное в знаменателе, называют определителем (или детерминантом) матрицы заданной системы и обозначают

(4.28) путем замены первого столбца столбцом из свободных членов, собственно ∆x2 - заменой второго столбца столбцом из свободных членов, а ∆x3 - третьего

столбца. Тогда формулы для нахождения решения системы (4.27), принимают вид

Эти формулы носят названия формул Крамера. Но исследованием систем линейных уравнений и методов их решений мы займемся с вами позднее, здесь же остановимся на, только что введенном, понятии определителя, обобщим это понятие на определитель n −го порядка, изучим свойства, которыми обладает определитель и методы его вычисления.

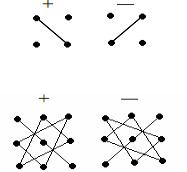
Итак, определителем квадратной матрицы называется алгебраическая сумма произведений элементов матрицы, причем эти произведения составляются по одному элементу из каждой строки и по одному элементу из каждого столбца. Все такие произведения входят в состав определителя, при этом знак таких произведений для определителя второго порядка определяется по схеме

для определителя третьего порядка

Для того чтобы определиться со знаками слагаемых при вычислении определителя произвольного, n −го порядка нам необходимо познакомиться с элементарными сведениями теории перестановок.

84

Две перестановки (α1, α2 , ..., αn ) и (β1, β2 , ..., βn ) называются равными, если αi = βi при i =1, n , В противном случае перестановки называют неравными

(различными).

Подсчитаем, напримерU ,U число различных перестановок из чисел 1, 2, 3, …, n . Так как на первом месте можно поместить любое из n данных чисел, на втором – любое из n −1 оставшихся чисел и т.д., то получаем n (n −1) (n − 2) K 2 1 различных перестановок.

Итак, число различных перестановок из чисел 1, 2, 3, …, n , равно произведению 1 2 3 ... (n −1) n , которое обозначается n! («эн факториал»).

Будем говорить, что два числа образуют инверсию в перестановке, если

бо′льшее число стоит левее ме′ньшего.

Например, в перестановке (1, 4, 5, 3, 2) инверсию образуют следующие пары чисел: 4 и 3; 4 и 2; 5 и 3; 5 и 2; 3 и 2. Итак, в рассматриваемой перестановке

зачеркиванием чисел, меньших αi (если таковые имеются).

НапримерU ,U найдем число инверсий в перестановке (3, 1, 2, 4):

Перед числом 1 стоит одно число, следовательно, k1 =1. Зачеркнем 1. Теперь перед числом 2 стоит одно число, следовательно, k2 =1. Аналогично получаем k3 = 0 (перед числом 3 не стоит ни одного числа). Следовательно, k (3, 1, 2,4) =1+1+0=2.

Заметим, что если числа в перестановке записаны в порядке возрастания, то число инверсий равно нулю.

Если число инверсий в перестановке четное, то она называется четной, в противном случае – нечетной.

Если в данной перестановке поменять местами два числа αi и α j при

условии, что остальные числа остаются на своих местах, то говорят, что новая перестановка получена из данной транспозицией чисел αi и α j .

Считают, две перестановки имеют разный характер четности, если одна из них – четная, а другая – нечетная.

Очевидны следующие утвержденияU :U

1. Пусть в некоторой перестановке сделана транспозиция. Она равна произведению нечетного числа транспозиций соседних элементов.

2. При транспозиции соседних элементов число инверсий в перестановке меняется на одну единицу.

3. Если в перестановке сделать транспозицию соседних элементов, то четность перестановки изменится на противоположную.

85

4. Любая транспозиция изменяет четность перестановки на противоположную.

Действительно, любая транспозиция равносильна нечетному числу

транспозиций соседних элементов.

5. Число четных перестановок n элементов равно числу нечетных перестановок.

6. Любая перестановка может быть получена из любой другой посредством нескольких транспозиций.

4.12 Определитель n -го порядка

Ранее была уже дана предварительная формулировка определителя, однако в этой формулировке отсутствовало правило, по которому определялись бы знаки слагаемых, входящих в определитель любого порядка. Это правило связано с разбиением перестановок (на четные и нечетные).

Приводим полную формулировку определителя.

Определителем квадратной матрицы называется алгебраическая сумма всевозможных произведений элементов этой матрицы, взятых по одному из каждой строки и по одному из каждого столбца. Сомножители в каждом слагаемом записываются в порядке следования строк, номера же столбцов образуют перестановки; слагаемые, соответствующие четным перестановкам, берутся со знаком «плюс», соответствующие нечетным – со знаком «минус».

Легко проследить, что расстановка знаков в определителях второго и третьего порядков соответствует сформулированному правилу.

В символической записи определитель можно записать так:

если нечетная.

Ясно, что понятие определителя имеет смысл для матриц с элементами из любого ассоциативного коммутативного кольца и, в частности, из любого поля. Вычислить определитель, например, 5 или 6-го порядка пользуясь этим определением очень затруднительно. Поэтому прежде чем говорить о правилах вычисления определителя n -го порядка рассмотрим теорему Лапласа, согласно которой вычисление определителя n -го порядка можно свести к вычислению определителей более низких порядков.

Теорема Лапласа

Введем несколько понятий.

86

Минором порядка k для этой матрицы называется определитель матрицы, составленной из элементов, находящихся на пересечении некоторых выбранных k строк и k столбцов. В общем виде минор порядка k можно записать в форме

aα1β1 ... aα1βk

... ... ... .

aαk β1 ... aαk βk

Здесь α1 , ..., αk - номера выбранных строк α1 < α2 < ... < αk , и β1 , ..., βk - номера выбранных столбцов β1 < β2 <... < β k .

Минором, дополнительным к данному минору порядка k , называется минор порядка n − k , матрица которого получается из исходной посредством вычеркивания строк и столбцов, содержащих данный минор порядка k .

Алгебраическим дополнением к данному минору называется дополнительный минор с множителем ( −1)α1+...+αk +β1+...+βk .

Теорема Лапласа Пусть в матрице определителя выбраны k строк. Определитель равен сумме произведений всех миноров порядка k , составленных из этих строк, на их алгебраические дополнения.

Например, если для определителя

выбрать первые две строки, теорема Лапласа дает

Доказательство теоремы Лапласа довольно громоздко. Поэтому мы опускаем его. Очень важным является частный случай теоремы Лапласа.

Рассмотрим ступенчатую матрицу A. Ступенчатая матрица устроена так:

87

Если к определителю ступенчатой матрицы применить теорему Лапласа,

то

Для приложений теории определителей теорема Лапласа, в основном, ценна именно в частном случае определителя ступенчатой матрицы.

НапримерU ,U вычислим определитель 7-го порядка.

В данном примере мы дважды применили теорему Лапласа к исходному определителю ступенчатой матрицы.

На основании теоремы Лапласа можно утверждать, что поскольку любой определитель n - го порядка сводится к вычислению определителей, например, второго или третьего порядков, то все свойства для определителей второго и третьего порядков справедливы и для определителя любого порядка.

Прежде чем заняться изучением свойств определителя, познакомимся с понятиями минора элемента определителя и алгебраического дополнения элемента определителя.

88

Минором элемента aij заданного определителя называется определитель,

полученный из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Минор элемента aik обозначается M ik .

НапримерU ,U минором элемента a21 определителя

a11 a12 a13

4.13 Свойства определителей

Свойства определителей второго и третьего порядков

Свойства определителей второго и третьего порядков выражаются следующими теоремами.

1. Определитель не изменится при замене всех его строк соответствующими столбцами.

Доказательство. Определитель третьего порядка, мы знаем, вычисляется следующим образом:

Теперь в определителе (4.30) каждую строку заменим столбцом с тем же номером, получим новый определитель

89

Сравнивая это равенство с предыдущим, заключаем, что определители равны, так как равны правые части указанных равенств.

2. При перестановке двух столбцов (строк) определитель меняет

знак.

Доказательство. В определителе (4.30) переставим, например, второй и третий столбцы, тогда

− a22 a33 a11 = −(a11 a22 a33 + a12 a23 a31 + a21 a32 a13 −

− a13a22a31 − a12a21a33 − a23a32a11 ).

Алгебраическая сумма в скобке равна правой части формулы (4.31). Следовательно, новый определитель отличается от исходного только знаком.

Другие случаи рассматриваются аналогично.

3. Определитель с двумя одинаковыми столбцами (строками) равен

нулю.

Доказательство. Определитель (4.30) обозначим через ∆. Пусть он содержит два одинаковых столбца. Переставив эти столбцы, получим тот же определитель ∆. По свойству 2 определитель при этом изменит знак, т.е. ∆ = −∆, откуда ∆ = 0 .

4. Множитель, общий для элементов некоторого столбца (строки), можно выносить за знак определителя.

Доказательство. Пусть в определителе (4.30) элементы, второго столбца имеют общий множитель λ , тогда

−λa12a21a33 −λa32a23a11 =λ( a11a22a33 +a12a23a31 +a21a32a13 −a13a22a31 −

Другие случаи рассматриваются аналогично.

5. Определитель с двумя пропорциональными столбцами (строками) равен нулю.

Доказательство. Действительно, выделяя общий множитель элементов одного из этих столбцов (коэффициент пропорциональности) и вынося его за знак определителя, получаем определитель с двумя одинаковыми столбцами, равный нулю.

90

6.Определитель равен нулю, если все элементы некоторого столбца (строки) равны нулю.

Доказательство. Если все элементы некоторого столбца (строки) равны нулю, то каждое слагаемое алгебраической суммы в правой части (4.31) равно нулю, как произведение, содержащее нулевой множитель.

7.Определитель не изменится, если к элементам некоторого столбца (строки) прибавить соответственные элементы другого столбца (строки), предварительно умножив их на один и тот же множитель.

Доказательство. Пусть, например, к элементам третьего столбца определителя (4.30) прибавлены соответственные элементы второго столбца, умноженные на множитель λ , тогда

Но второе слагаемое равно нулю, как определитель с одинаковыми столбцами, следовательно,

Одновременно доказано, что если в определителе все элементы

некоторого столбца (строки) равны суммам двух слагаемых, то такой определитель равен сумме двух определителей, т.е.

8. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Доказательство. Для определителя второго порядка теорема очевидна. Для определителя третьего порядка имеем:

т.к. вычленные определители есть алгебраические дополнения (см. определение

Aik ), т.е.

91

элементов a11 , a12 , a13 .

Формула (4.33) называется разложением определителя по элементам первой строки. Аналогично получается разложение по элементам других строк и столбцов.

9. Пусть ∆ - некоторый определитель третьего порядка. Сумма

произведений алгебраических дополнений элементов какой-нибудь строки (столбца) на любые числа q1 , q2 , q3 равна определителю ∆′, который

получается из данного ∆ заменой упомянутой строки (столбца) строкой (столбцом) из чисел q1 , q2 , q3 .

10. Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

Доказательство. Для определителя второго порядка теорема очевидна (получаем определитель с двумя одинаковыми строками).

a11 a12 a13

Пусть дан определитель третьего порядка ∆ = a21 a22 a23 . Покажем,

a31 a32 a33

например, что a11 A21 + a12 A22 + a13 A23 = 0 . В соответствии с только что доказанным свойством 9, следует

92