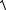Unlock-Линейная алгебра Сикорская 1
.pdf
случае
d = p0 − p = x0 cosα+ y0 sinα− p .
Если точки N и N 0 лежат по разные стороны от точки О, то нормальное уравнение прямой L0 имеет вид xcosα1 + y sinα1 − p0 =0, где α1 отличается от α на
π , т.е. α1 =π −α .
Следовательно, p0 = x0 cosα1 + y0 sinα 1=−x0 cosα − y0 sinα. В этом случае
d = p0 + p = x0 cosα+ y0 sinα− p .
Таким образом, в каждом из рассмотренных случаев получаем формулу
расстояния от точки до прямой:
d = |
|
x0 cosα+ y0 sinα− p |
|
. |
(7.21) |
|
|
Из формулы (7.21) следует, что для вычисления расстояния d от точки M0 до прямой L нужно в левую часть нормального уравнения поставить вместо (x, y) координаты точки M0 и полученное число взять по модулю.
Теперь покажем, как привести общее уравнение прямой к нормальному
виду. |
|
Пусть |
|
Ax+ By+C =0 |
(7.22) |
- общее уравнение некоторой прямой, а |
|
xcosα+ ysinα− p =0 |
(7.23) |
- ее нормальное уравнение.
Так как уравнения (7.22) и (7.23) определяют одну и ту же прямую, то их коэффициенты пропорциональны. Умножая все члены уравнения (7.22) на произвольный множитель µ ≠ 0 , получаем уравнение
µ Ax+µBy+µC =0.
При соответствующем выборе µ полученное |
уравнение обращается в |
|
уравнение (7.23), т.е. выполняются равенства |
|
|
µ A=cosα, µB =sinα, µC =−p. |
(7.24) |
|
Чтобы найти множитель µ , возведем первые |
два из этих равенств в |
|
квадрат и сложим, тогда получаем |
|
|
µ2 ( A2 + B 2 ) = cos 2 α + sin 2 α =1. |
|
|
Отсюда |
1 |
|
|
|
|
µ = ± |
A2 + B2 . |
(7.25) |
Число µ называется нормирующим множителем. Знак нормирующего множителя определяется с помощью третьего из равенств (7.24). Согласно этому равенству µС число отрицательное, если С ≠ 0 . А значит, в формуле (7.25)
берется знак, противоположный знаку С. Если С=0, то знак нормирующего множителя можно выбрать произвольно.
Рассмотрим еще один способ нахождения расстояния от точки до прямой.
169
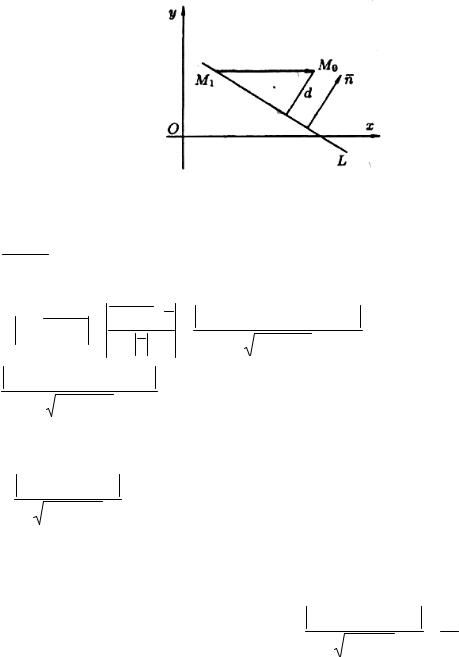
Пусть прямая L задана уравнением Ax+ By+C =0 и пусть точка не лежит на данной прямой M0 (x0 , y0 ) (рисунок 53). Найдем расстояние от точки M0 до прямой L.
Рисунок 53
Решение. Расстояние d от точки M0 до прямой L рано модулю проекции
вектора М1M0 , где М1(х1, у1) - произвольная точка прямой L, на направление нормального вектора. Следовательно,
d = пр M M |
0 |
= M1M0 n |
= ( x0 −x1 )A+( y0 − y1 )B = |
|
|
||
n |
1 |
|
n |
A2 +B2 |
|
|
|
|
|
|
|
|
|
||
= Ax0 +By0 − Ax1 −By1 . |
|
|
|
||||
|
A2 +B2 |
|
|
|
|
||
Так как точка М1(х1, у1) принадлежит прямой L, то |
Ax1 + By1 +C =0, |
т.е. |
|||||
C =−Ax1 −By1. Поэтому |
|
|
|
|
|||
d = Ax0 +By0 +C . |
|
|
(7.26) |
||||
A2 +B2 |
|
|
|
|
|||
Итак, формула |
d |
|
выражает расстояние от точки M0 (x0 , y0 ) до прямой |
L: |
|||
Ax+ By+C =0. |
|
|
|
|
|
|
|
Например, найдем расстояние от точки M0( 2,−1) до прямой 3x +4y −22=0. |
|||||||
Решение. По формуле (7.26), имеем d = 3 2 +4( −1) −22 |
= 20 =4. |
|
|||||
|
|
|
|
|
32 +42 |
5 |
|
Таким образом, расстояние от заданной точки до заданной прямой равно 4 единицам длины.
7.6 Линии второго порядка на плоскости
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
Ax2 +2Bxy+Cy2 +2Dx+2Ey+F =0. |
(7.27) |
Коэффициенты уравнения — действительные числа, и по крайней мере одно из чисел А, В, С отлично от нуля. Линии, задаваемые такими уравнениями
170
называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (7.27) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде, чем переходить к этому утверждению, изучим свойства перечисленных кривых.
1 Окружность
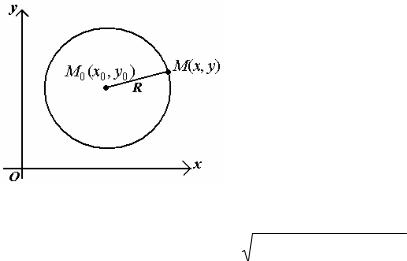
Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R c центром в точке M0 называется множество всех точек М
плоскости, удовлетворяющих условию M0М = R. Пусть точка M0 в прямоугольной системе координат Оху имеет координаты (х0 , у0 ), а M(х, у) - произвольная точка окружности (рисунок 54)
|
|
|
|
Рисунок 54 |
|
|
|
Тогда из условия M |
0 |
М = R получаем уравнение |
( х− х |
)2 +( у− у )2 |
= R, |
||
то есть |
|
|
|
0 |
0 |
|
|
)2 +( у− у )2 |
=R2 . |
|
|
|
|||
( х− х |
|
(7.29) |
|||||
0 |
0 |
|
|
|
|
|
|
Уравнению (7.29) удовлетворяют координаты любой точки M(х, у) данной
окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.
Уравнение (7.29) называется каноническим уравнением окружности.
Например, покажем, что уравнение x 2 + y 2 + 2x − 6 y −15 = 0 является
уравнением окружности, и найти ее радиус.
Преобразуем данное уравнение, приведя его к виду (7.29): (x 2 + 2x +1) + ( y 2 − 6 y + 9) −1 − 9 −15 = 0,
(x +1) 2 + ( y − 3) 2 = 25 .
Итак, данное уравнение есть окружность с центром в точке (-1,3) и радиусом 5.
2 Эллипс Эллипсом называется множество всех точек плоскости, сумма
расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
171
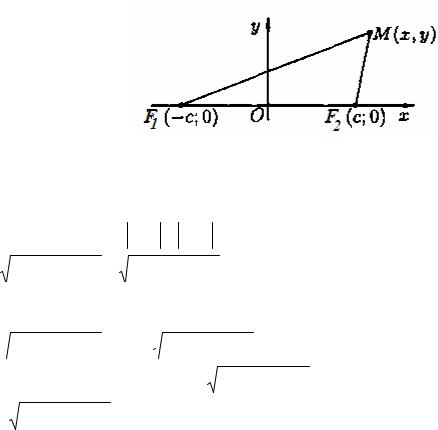
Обозначим фокусы через F1 и F2, расстояние между ними через 2с, а
сумму расстояний от произвольной |
точки эллипса до |
фокусов — через 2а, |
(рисунок 55). По определению 2а > 2с, т. е. а> с. |
|
|
Для вывода уравнения эллипса выберем систему координат Оху так, чтобы |
||
фокусы F1 и F2 лежали на оси Ох, |
а начало координат совпадало с серединой |
|
отрезка F1 F2. Тогда фокусы будут |
иметь следующие |
координаты; F1(−с,0) и |
F2(с, 0). |
|
|
Рисунок 55
Пусть M(х, у) — произвольная точка эллипса. Тогда, согласно определению эллипса, MF1 + MF2 =2a, т. е.
(x +c)2 + y2 + (x −c)2 + y2 =2a |
(7.30) |
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (7.30) к более простому виду следующим образом:
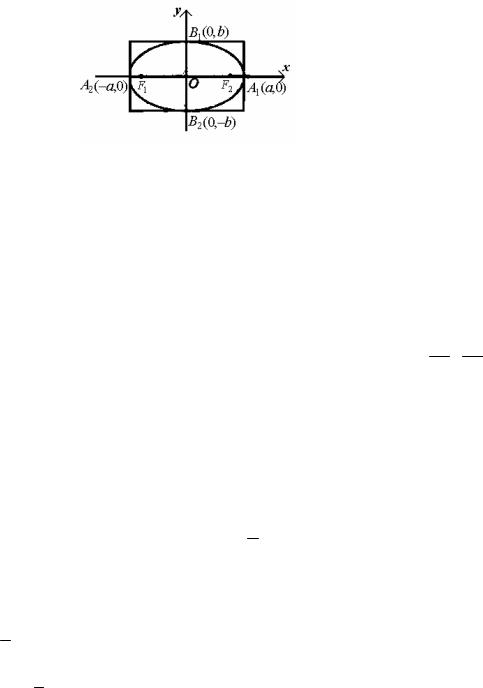
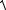 (x +c)2 + y2 =2a −
(x +c)2 + y2 =2a −  (x −c)2 + y2 ,
(x −c)2 + y2 ,
x2 +2cx+c2 + y2 =4a2 −4a (x −c)2 + y2 + x2 −2cx +c2 + y2 , a (x −c)2 + y2 =a2 −cx,
a2 x2 −2a2cx+a2c2 +a2 y2 =a4 −2a2cx+c2 x2 , (a2 −c2 )x2 +a2 y2 =a2 (a2 −c2 ).
Так как a >c , то a2 −c2 >0. Положим a2 −c2 =b2
Тогда последнее уравнение примет вид b2 x2 +a2 y2 =a2b2 или
x2 |
+ |
y2 |
=1. |
(7.31) |
|
a2 |
b2 |
||||
|
|
|
Можно доказать, что уравнение (7.31) равносильно исходному уравнению.
Уравнение (7.31) называется каноническим уравнением эллипса.
Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1 Уравнение (7.31) содержит х и у только в четных степенях, поэтому если
172
точка (х,у) принадлежит эллипсу, то ему также принадлежат точки (х,-у), (-х,у), (-х,-у). Отсюда следует, что эллипс симметричен относительно осей Ох и Оу, а также относительно точки О(0,0), которую называют центром эллипса.
2 Найдем точки пересечения эллипса с осями координат. Положив у=0, находим две точки А1(−а,0) и А2(а,0), в которых ось Ох пересекает эллипс
(рисунок 56). Положив в уравнении (7.31) х=0, находим точки пересечения эллипса с осью Оу: В1(0,−b) и B2 (0,b). Точки А1, A2 , B1, B2 называются вершинами
эллипса. Отрезки А1A2 , B1B2 , а также их длины 2а и 2b называются
соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
Рисунок 56
3 Из уравнения (7.31) следует, что каждое слагаемое в левой части не
превосходит единицы, т. е. имеют |
место неравенства |
х2 |
≤1, |
у2 |
|
а |
2 |
2 |
|||
−a ≤ x ≤a, −b ≤ y ≤b. Следовательно, |
|
|
|
b |
|
все точки эллипса |
|
лежат |
|||
прямоугольника, образованного прямыми x =±a, y =±b.
≤1 или внутри
4В уравнении (7.31) сумма неотрицательных слагаемых х2 , у2 равна
а2 b2
единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если |х| возрастает, то |у| уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму, изображенную на рисунке 56 (овальная замкнутая кривая).
Дополнительные сведения об эллипсе
b
Форма эллипса зависит от отношения а. При b= а эллипс превращается в
окружность, уравнение эллипса (7.31) принимает вид x2 + y2 =a2 .
В качестве характеристики формы эллипса часто пользуются соотношением аc .
Отношение аc половины расстояния между фокусами к большой полуоси
173
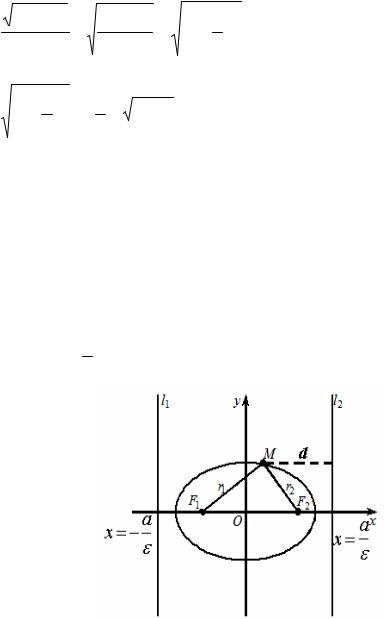



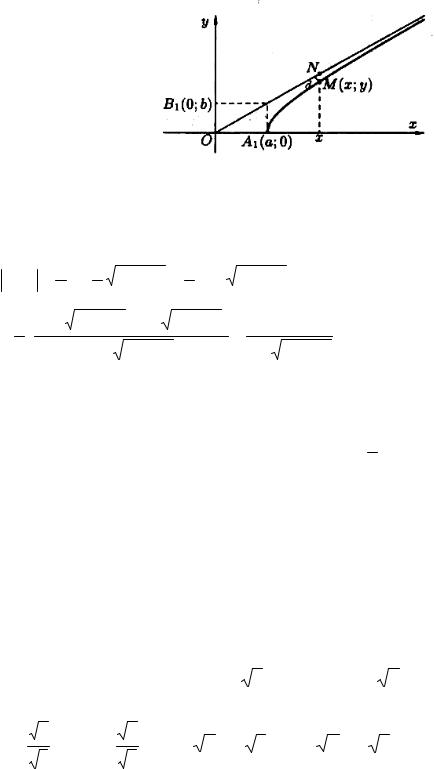
Рисунок 61
Найдем расстояние MN разности между ординатами прямой и ветви гиперболы:
MN = b x −b x2 −а2 |
= b |
(x − x2 |
−a2 ) = |
|
|||||||
|
|
|
a |
a |
|
a |
|
|
|
|
|
= |
b |
|
(x − x2 |
−a2 )(x + |
|
x2 −a2 ) |
= |
|
ab |
. |
|
a |
x + x2 −a2 |
|
|
|
x2 −a2 |
||||||
|
|
|
|
x + |
|
||||||
Как видно, по мере возрастания х знаменатель дроби увеличивается; числитель — есть постоянная величина. Из чего заключаем, что длина отрезка MN стремится к нулю. Так как MN больше расстояния d от точки М до прямой, то
d и подавно стремится к нулю. Итак, прямые y =±ab x являются асимптотами
гиперболы (7.34).
Например, найдем уравнение асимптот гиперболы 2x 2 − 3y 2 = 6 .
У гиперболы (7.34) две асимптоты, определяемые уравнениями (7.35). Для начала найдем a и b заданной гиперболы.
Приведем уравнение гиперболы к каноническому виду, разделив при этом обе его части на 6. Получим
|
x2 |
|
− |
y2 |
=1. |
|
|
|
|
3 |
|
2 |
a 2 = 3 a = |
3, b2 = 2 b = |
|
||||
|
|
|
|
||||||
Таким образом, |
2 . Подставляя найденные |
||||||||
эти значения a, b в уравнения асимптот (7.35), получаем |
|||||||||
|
y = |
|
2 x, y =− |
2 x или |
2x − |
3y = 0, 2x + |
3y = 0 . |
||
|
|
|
|
3 |
|
3 |
|
|
|
При построении гиперболы (7.34) целесообразно сначала построить основной прямоугольник гиперболы (рисунок 62), провести прямые, проходящие через противоположные вершины этого прямоугольника, — асимптоты
гиперболы и отметить вершины А1, А2 гиперболы.
178