Unlock-Линейная алгебра Сикорская 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный университет»

Г.А. СИКОРСКАЯ

КУРС ЛЕКЦИЙ ПО АЛГЕБРЕ И ГЕОМЕТРИИ

Рекомендовано Ученым советом государственного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет» в качестве учебного пособия для студентов транспортного факультета

Оренбург 2007

3

УДК 512/514 (07)

ББК 22.14+22.15я73 С 35

Рецензенты кандидат физико-математических наук Герасименко С.А.

кандидат педагогических наук Липилина В.В.

Сикорская Г.А.

С35 Курс лекций по алгебре и геометрии: учебное пособие для студентов транспортного факультета / Г.А. Сикорская, Оренбург: ГОУ ОГУ, 2007. - 387 с.

ISBN

Пособие подготовлено в соответствии с содержанием курса «Алгебра и геометрия», определяемым образовательным стандартом высшего профессионального образования.

Пособие состоит из 15 глав, каждая из которых включает в себя относительно самостоятельную теоретическую часть курса, обычно разделяемую преподавателем на 3 – 4 лекции.

Излагаемые теоретические вопросы курса алгебры и геометрии снабжены задачами практического характера, способствующими лучшему пониманию теории. В заключении каждой главы предлагаются вопросы для самоконтроля.

Учебное пособие предназначено для студентов специальностей 190601

– Автомобили и автомобильное хозяйство, 190603 – Сервис транспортных и технологических машин и оборудования (по отраслям), 190702 – Организация и безопасность движения, 200503 – Стандартизация и сертификация, 220501 – Управление качеством.

4

Содержание

Введение………………………………………………………………………... 7

Глава 1 Первоначальные сведения об основных алгебраических структурах……………………………………………………………………… 8

1.1Множества. Основные понятия……………………………………. 8

1.2Операции над множествами и их свойства……………………...... 10

1.3 Отношения на множествах………………………………………… 17

1.4Отображение множеств…………………………………………...... 18

1.5Необходимые сведения о группах, кольцах, полях………………. 21

2.1Система комплексных чисел……………………………………..... 25

2.2Определение комплексных чисел. Операции над комплексными числами алгебраической формы………………………………………. 26

2.3Тригонометрическая форма комплексных чисел. Операции над комплексными числами, заданными в тригонометрической форме... 33

2.4Корни из единицы…………………………………………………... 41

2.5Показательная и логарифмическая функции комплексной переменной……………………………………………………………… 43

3.1Действия над многочленами……………………………………...... 47

3.2Свойства делимости многочленов……............................................ 51

3.3.Корни многочлена. Теорема Безу…………………………………. 52

3.7Формулы Вьета…………………………………………….……….. 57

3.8Многочлены с действительными коэффициентами. Разложение

4.3Умножение матриц…………………………………………………. 69

4.4Многочлен от матрицы…………………………………………….. 73

4.5Транспонирование матриц…………………………………………. 74

4.6Симметрическая матрица, кососимметрическая матрица……...... 75

4.7Обратная матрица…………………………………………………... 76

4.8Ортогональная матрица…………………………………………..... 77

4.13Свойства определителей………………………………………...... 86

4.14Методы вычисления определителей n -го порядка……………... 91

4.15Определитель произведения матриц……………………………... 95

5

4.16Методы нахождения обратных матриц………………………….. 99

4.17Простейшие матричные уравнения………………………………. 101

4.18Ранг матрицы………………………………………………………. 102

4.19Методы вычисления ранга матрицы……………………………... 103

4.20Базисный минор матрицы………………………………………… 107

4.21Вопросы для самоконтроля……………………………………….. 108 Глава 5 Системы линейных уравнений………………………………………. 110

5.1 Системы линейных уравнений. Основные понятия……………… 110

5.2Метод Гаусса………………………………………………………... 112

5.3Решение невырожденных систем линейных уравнений.

Формулы (теорема) Крамера……………………………………..…..... 116

5.4 Решение систем линейных уравнений матричным способом…… 119

5.5Критерий совместности системы линейных уравнений…………. 120

5.6Базисные неизвестные системы линейных уравнений. Способ решения неопределенной системы…………………………………..... 123

5.7Системы линейных однородных уравнений. Фундаментальная система решений………………………………………………………... 125

5.8Вопросы для самоконтроля………………………………………… 130

Глава 6 Векторная алгебра……………………………………………………. 132

6.1 Векторы. Основные понятия. Линейные операции над векторами………………………………………………………………... 132 6.2 Проекция вектора на ось…………………………………………… 135

6.3Линейная зависимость и линейная независимость векторов. Свойства линейно зависимой системы векторов……………………... 137

6.4Базис системы векторов. Координаты вектора относительно базиса…………………………………………………………………..... 139

6.5Ортонормированный базис. Направляющие косинусы вектора.

Длина вектора…………………………………………………………… 141

6.6Скалярное произведение векторов и его свойства……………...... 143

6.7Векторное произведение векторов и его свойства……………...... 145

7.4Уравнение линии на плоскости……………………………………. 159

7.5Линии первого порядка на плоскости……………………………... 162

7.6Линии второго порядка на плоскости…………………………….. 170

7.7Вопросы для самоконтроля……………………………………........ 188

Глава 8 Аналитическая геометрия в пространстве………………………….. 190

8.1Аффинная и прямоугольная декартовы системы координат.

Простейшие задачи……………………………………………………... 190

8.2Уравнение поверхности и линии в пространстве……………........ 192

8.3Уравнение плоскости в пространстве……………………………... 194

8.4Плоскость. Основные задачи………………………………………. 198

8.5Уравнения прямой в пространстве……………………………........ 201

8.6Прямая в пространстве. Основные задачи……………................... 204

8.7Прямая и плоскость в пространстве. Основные задачи………….. 205

6

8.8 Уравнение цилиндрической поверхности с образующей, параллельной координатной оси. Цилиндры второго порядка……… 209

8.9Уравнение поверхности вращения……………………………........ 212

8.10Поверхности второго порядка……………………………………. 213

8.11Вопросы для самоконтроля……………………………………….. 220

Глава 9 Линейное пространство. Подпространство линейного пространства…………………………………………………………………… 222

9.1Понятие линейного пространства…………………………………. 222

9.2Линейная зависимость векторов..………………………………..... 224

9.3Размерность и базис линейного пространства……………………. 227

9.4 Ранг системы векторов линейного пространства………………… 230

9.5Матрица перехода от базиса к базису. Преобразование координат вектора………………………………………………………. 231

9.6Изоморфизм линейных пространств………………………………. 234

9.7Подпространство линейного пространства……………………...... 235

9.8Линейная оболочка системы векторов……………………………. 236

9.9Пересечение подпространств. Сумма подпространств…………... 240

9.10Вопросы для самоконтроля……………………………………...... 245

Глава 10 Евклидово и унитарное пространство…..……………………......... 247

10.1Определение евклидовых пространств…………………………... 247

10.5Ортонормированный базис……………………………………...... 252

10.6Выражения скалярного произведения через координаты векторов в ортонормированном базисе……………………………...... 253

10.7Понятие унитарного пространства……………………………...... 254

10.8Изоморфизм евклидовых (унитарных) пространств……………. 257

10.9Унитарные матрицы………………………………………………. 258

10.10Вопросы для самоконтроля……………………………………… 259

Глава 11 Линейные операторы……………………………………………….. 260

11.1 Линейный оператор. Основные определения…………………… 260

11.2Связь между координатами вектора и его образа………………. 262

11.3Преобразование матрицы линейного оператора при переходе к новому базису…………………………………………………………… 264

11.4Ядро и область значений линейного оператора…………………. 266

11.5Характеристический многочлен, характеристическое уравнение линейного оператора………………………………..……… 267

11.6 Минимальный многочлен матрицы……………………………… 270

11.7Собственные векторы линейного оператора…………………...... 271

11.8Собственные значения и собственные векторы симметрической матрицы……………………………………………… 273

11.9Диагонализируемость линейного оператора…………………….. 275

11.10Действия над линейными операторами..………………………. 277

11.11Оператор, обратный данному линейному оператору………….. 281

11.12Ортогональные матрицы*……………………………………….. 281

11.13Ортогональные операторы………………………………………. 284

11.14Вопросы для самоконтроля……………………………………… 286

7

12.2Преобразование квадратичной формы линейным однородным оператором……………………………………………............................ 290

12.3Нормальный вид квадратичной формы………………………...... 295

12.6Приведение квадратичной формы к каноническому виду……... 300

12.7Применение теории квадратичных форм в задачах о приведении к каноническому виду уравнения кривой второго порядка и уравнения поверхности второго порядка…………………. 305

12.8Вопросы для самоконтроля……………………………………...... 310

Глава 13 Геометрические объекты дифференциальной геометрии………... 312

13.1Кривые. Способы задания кривых……………………………...... 312

13.2О касательных и нормалях………………………………………... 314

13.3Кривизна линий. Радиус и центр кривизны. Натуральное уравнение кривой……………………………………………………..... 317

13.4Эволюта. Эвольвенты……………………………………………... 321

13.5Соприкасающаяся плоскость……………………………………... 325

13.6Кривизна кривой…………………………………………………... 327

13.7Подвижный триедр………………………………………………... 330

13.8Кручение кривой…………………………………………………... 331

13.9Формулы Френе-Серре……………………………………………. 334

14.1Способы аналитического изображения поверхностей………...... 336

14.2Касательная плоскость и нормаль к поверхности………………. 337

14.3Первая квадратичная форма поверхности……………………...... 342

14.4Вторая квадратичная форма поверхности……………………...... 346

14.5Вопросы для самоконтроля……………………………………...... 347 Глава 15 Топология……………………………………………………………. 348

15.1Что такое топология?........................................................................ 348

15.2Обобщение понятий пространства и функций………………….. 352

15.3От метрического пространства к топологическому…………...... 355

15.4Понятие римановой поверхности………………………………… 365

15.5Вопросы для самоконтроля……………………………………...... 370

Список использованных источников………………………………………… 372

8

Введение

Курс алгебры и геометрии, читаемый студентам транспортного факультета (параллельно с курсом математического анализа) опирается на базовый курс математики, изучаемый в средней школе.

Курс математики в высшей школе призван заложить основы математической подготовки будущих инженеров, дающие возможность успешного освоения других математических дисциплин: теории вероятностей, математической статистики, численных методов, а также, умения использовать математические методы при изучении специальных дисциплин.

Математическое образование будущего инженера основывается на фундаментальных понятиях математики. Фундаментальность подготовки в области математики включает в себя достаточную общность математических понятий и конструкций, обеспечивающую широкий спектр их применимости, точность формулировки математических свойств изучаемых объектов, логическую строгость изложения математики, опирающуюся на адекватный современный математический аппарат.

Курс алгебры и геометрии представляет собой математическую теорию, охватывающую первоначальные сведения об основных алгебраических структурах, теорию матриц и определителей, векторную алгебру, теорию линейных и евклидовых пространств, теорию линейных операторов, аналитическую геометрию, дифференциальную геометрию и топологию.

В результате теоретической части курса студент приобретает знания основных понятий дисциплины, понимание и умение доказательства теории, навыки решения математических задач методами линейной и векторной алгебры с доведением решения до практически приемлемого результата (формулы, числа, графика, качественного вывода и т.д.), на базе чего развивается логическое и алгоритмическое мышление, навыки математического исследования прикладных вопросов (перевод реальной задачи на математический язык, выбор оптимального метода ее решения и исследования, интерпретация и оценка полученных результатов и т.п.).

Изучение курса алгебры и геометрии способствует формированию понимания необходимости математической составляющей в общей подготовке, представления о роли и месте математики в современной цивилизации и в мировой культуре, умения оперировать абстрактными объектами, корректно использовать математические понятия и символы для выражения количественных и качественных отношений.

Курс алгебры и геометрии изучается на первом и втором семестрах обучения.

Промежуточная оценка знаний и умений проводится с помощью тестовых задач, а также с помощью коллоквиумов. Итоговый контроль предусмотрен в виде зачета.

9

Глава 1 Первоначальные сведения об основных алгебраических структурах

Данная глава носит вспомогательный характер. В ней приводится в систему, уточняется и расширяется материал по некоторым общим вопросам, затрагиваемым в школьной математике, в частности, излагаются простейшие сведения о множествах и операциях над ними, о подмножествах и отображениях множеств, а также происходит обзорное знакомство читателя с основными алгебраическими структурами. Всё перечисленное необходимо для изучения остальных глав пособия.

При доказательствах утверждений данного пособия, в основном, используются известные из средней школы методы доказательства: метод непосредственной проверки, метод от противного и метод полной математической индукции.

Напомним, что методом полной математической индукции доказываются утверждения, содержащие переменный параметр п, принимающий значения 1, 2, 3, …. Процесс доказательства состоит из двух этапов. На первом этапе устанавливается, что доказываемое утверждение верно при n =1, на втором – доказывается, что из его истинности для n = m (при любом фиксированном т) следует его истинность для n = m +1. Первый этап называется началом индукции,

второй – индуктивным переходом от п к п+1.

1.1 Множества. Основные понятия

Во всех областях современной математики, за исключением узко специальных ее разделов, связанных с аксиоматическим построением теории множеств, понятие множества принято считать основным, неопределяемым понятием. Создатель теории множеств немецкий математик Г. Кантор (1845 – 1918) пояснил понятие множества следующим образом: «Множество, или совокупность - это собрание определенных и различных объектов нашей интуиции или интеллекта, мыслимое в качестве единого». Говорят также, что множество – это совокупность, собрание, или семейство каких-либо реально существующих или мыслимых объектов. Предполагается, что объекты, входящие в множество, попарно различны. Объекты, из которых составлено множество, называются его элементами.

Множества задаются двумя способами:

1)перечислением всех элементов множества;

2) указанием характеристического свойства элементов данного множества, т.е. такого свойства, которым обладают элементы данного множества

a, b, c,..., x, y, .... Знак множества - { }.

10

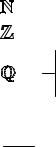
Например: а) A ={− 3; 3} - конечное, двухэлементное множество.

x2 − 9 = 0 (т.е. множество корней уравнения x2 − 9 = 0 ).

На основании этого примера можно сделать вывод, что одно и тоже множество может быть задано разными характеристическими свойствами.

a A означает «элемент а принадлежит множеству А». a A - «элемент а не принадлежит множеству А».

Множество, не содержащее ни одного элемента, называется пустым, и обозначается символом .

Два множества называются равными, если они состоят из одних и тех же элементов.

Так, в приведенном выше примере, множества A и A1 равные.

Для некоторых, часто используемых и известных из средней школы числовых множеств, существуют стандартные обозначения:

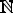= {1, 2, 3, K} - множество целых неотрицательных чисел (или множество

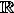– множество действительных чисел (или вещественных) чисел, т.е. чисел, представимых бесконечными десятичными периодическими дробями;

m, n (для m, n 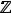, m < n ) – множество {m, m +1, ..., n}.

Если каждый элемент множества А является элементом множества В, то говорят, что А есть подмножество множества В (или В включает А), и пишут

A B .

В частности, любое множество является подмножеством самого себя, т.е.

A A.

Пустое множество считается подмножеством любого множества А, т.е.

A.

Очевидно, что множества A, B равны тогда и только тогда, когда A B и

B A. Если A B и A ≠ B , то говорят, что B строго включает А, или А является собственным подмножеством множества В.

В повседневной практике нам часто приходится получать из одних множеств другие, например, объединяя заданные множества, выбирая из них общие или, наоборот, необщие элементы, и т.д. Для формализации таких способов получения множеств используются различные операции над множествами: пересечение, объединение, вычитание, дополнение и декартово произведение.

11

1.2 Операции над множествами и их свойства

Пересечение множеств

Пересечением множеств А, В называется множество A ∩ B , состоящее из

непересекающимися.

Пересечение множеств можно проиллюстрировать, используя, так называемые, круги Эйлера-Венна (здесь и далее U – универсальное множество, т.е. множество, которое содержит в себе все слагаемые, перемножаемые и т.д. множества).

Рисунок 1 Из рисунка 1 видно, что пересечением множеств является их общая часть.

Приведем примеры пересечения множеств:

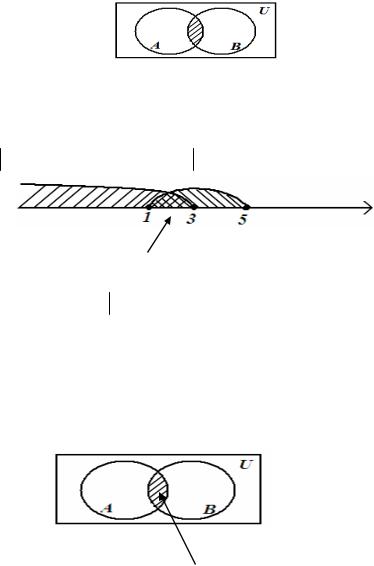
1) A ={x x R и 1 ≤ x ≤ 5}, B ={x x R и x ≤ 3}.

С

Рисунок 2

Имеем, С = A ∩ B ={x x R и1 ≤ x ≤ 3}.

2) А – множество треугольников на плоскости.

В – множество правильных многоугольников на плоскости.

Тогда A ∩ B - множество правильных треугольников на плоскости.

Свойства операции пересечения множеств

1) A ∩ B = B ∩ A - коммутативность пересечения.

A ∩ B = B ∩ A

Рисунок 3

12