
Unlock-Линейная алгебра Сикорская 1
.pdf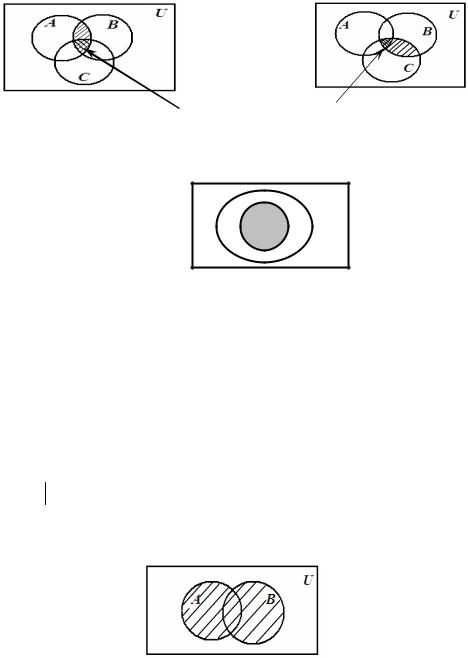
2) (A ∩ B)∩C = A ∩(B ∩C) - ассоциативное свойство пересечения.
(A ∩ B)∩C = A ∩(B ∩C)
Рисунок 4
3) Если B A, то A ∩ B = B .
U
A
B
Рисунок 5
4) A ∩ = , A ∩ A = A .
Объединение множеств
Объединением множеств А, В называется множество A B , состоящее из всех тех элементов, каждый из которых принадлежит хотя бы одному из множеств A, B . Это множество обозначают C = A B , т.е.
C = A B ={x x A или x B}.
Используя круги Эйлера-Венна, объединение множеств А и В можно проиллюстрировать следующим образом:
Рисунок 6
Свойства операции объединения множеств
1)A B = B A - свойство коммутативности.
2)(A B) C = A (B C) - свойство ассоциативности.
3)Если B A, то A B = A .
13
U
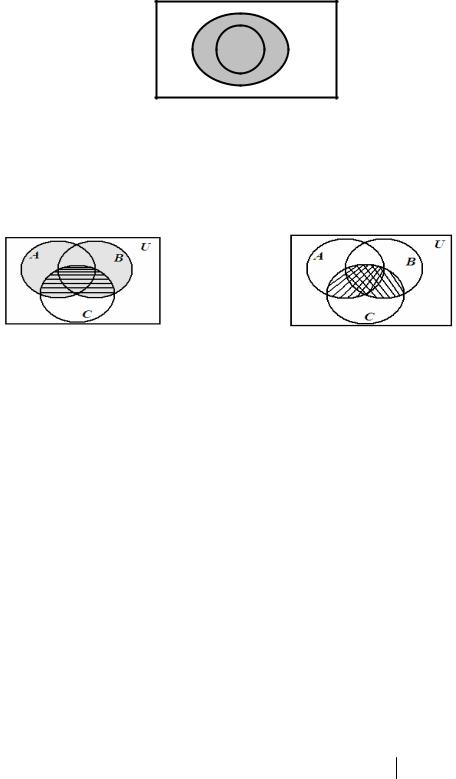
A B
Рисунок 7
4)A = A , A A = A .
5)(A B)∩C = (A ∩C) (B ∩C) - свойство дистрибутивности.
Проиллюстрируем свойство дистрибутивности на кругах Эйлера-Венна:
(A B)∩C |
(A ∩C) (B ∩C) |
|
Рисунок 8 |
Докажем свойство дистрибутивности. |
|
Определимся, для |
того, чтобы доказать равенство двух множеств, |
необходимо показать, что каждый элемент первого множества принадлежит
второму и обратно – каждый элемент второго множества принадлежит первому. |
|
Пусть x (A B)∩ C x A B и x C (x A или x B) и x C |
|
(x A и x C) или (x B и x C) (x A ∩C) или (x B ∩C) |
|
x (A ∩C) (B ∩C) - что и требовалось доказать. |
|
Таким образом, всякий элемент х из левого множества одновременно принадлежит и правому множеству. Доказательство обратного утверждения предлагаем читателю выполнить самостоятельно.
Дополнение
Операция дополнения определена лишь в случае, когда все изучаемые множества рассматриваются как подмножества некоторого универсального множества U.
Пусть A U . Дополнением к А называют множество всех элементов из U, не принадлежащих А. Дополнение обозначают A′: A′ ={x x U и x A}.
Например, рассмотрим U = Z - множество целых чисел и А – множество нечетных чисел. Тогда A′ есть множество четных чисел.
Или, например, пусть U - множество точек круга, а А – множество точек границы этого круга, (т.е. множество точек окружности), тогда A′ - открытый круг.
14
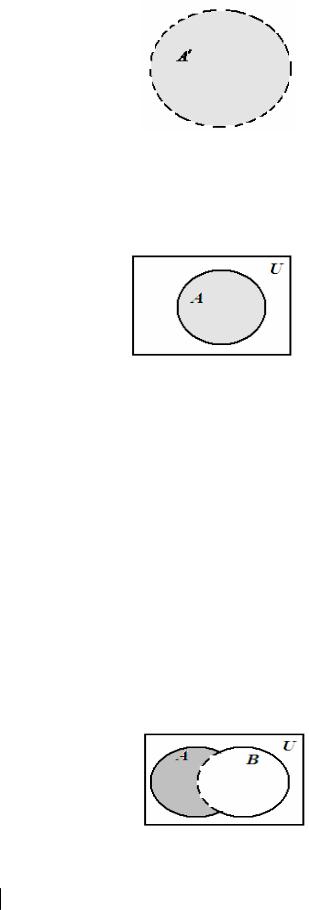
Рисунок 9
Свойства операции дополнения
1) (A′)′ = A.
Рисунок 10
2) |
|
′ |
′ |
. |
|
|
|
B A → A B |
′ |
′ |
. |
||||
|
|
|
|
|
|||
Доказательство: Если x A |
x A x B (т.к. B A) x B |
||||||
3) |
′ =U . |
|
|
|
|
|
|
4) |
U ′ = . |
|
|
|
|
|
|
|
′ |
′ |
|
′ |
. |
|
|
5) (A I B) |
= A |
B |
|
|
|||
|
′ |
′ |
|
′ |
. |
|
|
6) (A B) |
= A |
∩ B |
|
|
|||
Предлагаем читателю самостоятельно убедиться в справедливости свойств операции дополнения на кругах Эйлера-Венна.
Разность двух множеств
Разностью двух множеств А и В называют множество A \ B элементов х таких, что х принадлежит А и не принадлежит В.
Рисунок 11
A \ B ={x x A и x B}.
Например, пусть заданы два числовых множества A = {0; 1; 3; 8; 13} и B ={−1; 0; 1; 7; 13}, тогда разностью A \ B будет множество, содержащее только те
15

элементы множества А, которые не являются элементами множества В, т.е.
A \ B ={3; 8}.
Помимо операций объединения, пересечения, разности и дополнения, существует еще декартово произведение множеств, определить которое мы можем, введя понятие кортежа.
Кортежи. Декартово произведение множеств
Итак, пусть даны множества A1, A2 , ..., An . Выберем из первого множества элемент a1 , из второго - a2 и т.д., из множества An выберем элемент an .
Расположим элементы в порядке их извлечения. Получим упорядоченную последовательность (a1, a2 , ..., an ).
Упорядоченная последовательность (a1, a2 , ..., an ), составленная из элементов множеств A1, A2 , ..., An , где ai Ai , i =1,2,..., n , называется кортежем
длины п.
Заметим, что множества A1, A2 , ..., An могут иметь общие элементы или
даже совпадать. Поэтому (в отличие от обычного множества) элементы в кортеже |
|||||||||||
могут повторяться. |
|
|
|
|
|
|
|
|
|
|
|
Элементы a1, a2 , ..., an кортежа (a1, a2 , ..., an ) называются его |
|||||||||||
компонентами или координатами. |
|
|
|
|
|
|
|||||
Два кортежа, составленные из элементов одного и того же множества А |
|||||||||||
считаются |
равными, |
если |
их |
длины |
равны |
и |
элементы, |
стоящие |
на |
||
|
|
|
|
|
|
|
|
|
|
m = n, |
|
соответствующих местах, |
равны, |
т.е. (a1, a2 , ..., am )= (b1, b2 , ..., bn ) |
|
|
|
||||||
ak =bk , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ai A, bj A, i =1, 2,...,m, |
j =1, 2, ..., n . |
|
|
|
|
1 ≤ k ≤ n, |
|||||
( 1, |
|
81) равны, |
|
|
|||||||
Например, кортежи |
(12 , 22 32 ) и |
16, |
поскольку |
||||||||
12 = 1, 22 = |
16, 32 = |
81 , |
тогда как кортежи (1, 2, 3) |
и (3, 1, 2) различны, |
хотя |
||||||
имеют одинаковую длину и одно и тоже множество координат, но эти координаты стоят в разном порядке. Различны и кортежи (1, 2, 3) и (1, 2, 3, 4) -
они имеют разную длину.
Координатами кортежа могут быть множества, кортежи и т.д. При этом, например, кортежи ({a, b}, c) и ({b, a}, c) равны, так как {a, b}={b, a}, а кортежи
((a,b), c) и ((b, a), c) различны, так как (a, b) ≠ (b, a) . (Поясним {a, b} -
множество, (a, b) - кортеж).
Кортеж, не содержащий ни одной координаты (т.е. кортеж длины 0), называется пустым.
Подчеркнем еще раз отличия понятий кортежа и множества:
а) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны даже в случае, если они имеют одинаковый состав;
16

б) в множестве все элементы различны, а в кортеже координаты могут повторяться.
Чтобы различать множества и кортежи, элементы множеств заключают в фигурные скобки, а элементы кортежей – в круглые (в частности, в круглые скобки заключают элементы UупорядоченныхU множеств).
Введем теперь понятие декартова произведения множеств.
Пусть A1, A2 , ...., An - некоторые множества. Их декартовым
произведением называют множество, состоящее из всех кортежей вида (a1, ..., an ) , где ak Ak , 1 ≤ k ≤ n . Декартово произведение множеств A1, A2 , ...., An
обозначают A1 ×.... × An .
НапримерU ,U если A ={1,2, 3}, B ={x, y}, то
A × B ={(1, x), (1, y), (2, x), (2, y), (3, x), (3, y)} и B × A ={(x,1), (x, 2), (x,3), ( y,1), ( y, 2), ( y, 3)}.
Этот пример показывает, что, вообще говоря, декартовы произведения A × B и B × A различны, хотя они содержат поровну элементов.
Различны и множества A × B ×C , (A × B)×C и A ×(B ×C) - первое состоит из троек (a, b, c), второе – из пар вида ((a, b), c), а третье – из пар вида (a, (b, c)),
где во всех случаях a A, b B , c C .
Если хотя бы одно из множеств А, В пусто, то считают, что их декартово
произведение пусто:
A × = × A = × = .
НапримерU ,U декартово произведение R × R состоит из пар (x, y) действительных чисел, причем (x1, y1 )= (x2 , y2 ) в том и только в том случае,
когда |
x1 = x2 , |
y1 = y2 . |
Каждой |
такой |
паре |
соответствует |
точка |
M (x, y) |
на |
|||
плоскости, |
для |
которой числа |
x и |
y |
являются декартовыми координатами |
|||||||
(отсюда название «декартово произведение»). Декартово произведение R × R× R |
||||||||||||
состоит из троек чисел (x, y, z) , |
которые можно рассматривать как координаты |
|||||||||||
точки |
M (x, y, z) в |
трехмерном |
пространстве. |
Декартово |
произведение |
|||||||
R × R×...× R |
(п множителей) называют п-мерным арифметическим |
|||||||||||
пространством. Его обозначают Rn . |
|
|
|
|
|
|
|
|||||
|
Пусть А – произвольное множество и п – натуральное число. Декартовой |
|||||||||||
п-ой степенью множества А называется множество, обозначаемое через An |
и |
|||||||||||
состоящее |
из |
всевозможных |
кортежей |
длины |
п |
элементов из |
А: |
|||||
An ={(a1,...,an )ai A, i 1,n}.
В заключение перечислим основные свойства операций над множествами, обозначая буквами А, В, С произвольные множества.
1)A B = B A (коммутативность операции );
2)A ∩ B = B ∩ A (коммутативность операций ∩);
3)(A B) C = A (B C) (ассоциативность операции );
4)(A ∩ B)∩C = A ∩ (B ∩C) (ассоциативность операции∩);
5)A A = A (идемпотентность операции );
17
6)A ∩ A = A (идемпотентность операции ∩);
7)A (A ∩ B)= A ;
8)A ∩ (A B)= A ;
9)(A B)∩C = (A ∩C) (B ∩C);
10)(A B) C = A (B C);
11)(A B)\ C = (A \ C) (B \ C);
12)(A ∩ B)\ C = (A \ C)∩ (B \ C);
13)(A B)×C = (A ×C) (B ×C);
14)(A ∩ B)×C = (A ×C)∩ (B ×C);
15)A \ (B C)= (A \ B)∩ (A \ C);
16)A \ (B ∩C)= (A \ B) (A \ C);
17)A \ (B C)= (A \ B)\ C ;
18)A \ (A B)= ;
19)A \ (A ∩ B)= A \ B ;
20)A = A ;
21)A ∩ = .
Свойства 7), 8) называются законами поглощения, свойства 9) – 14) –
законами правой дистрибутивности операций умножения, сложения,
вычитания и декартова произведения ( ∩, , \, ×), относительно операций сложения и умножения ( , ∩).
Справедливость выписанных равенств следует непосредственно из определений операций над множествами и легко проверяется. Так, проверку равенства 12) можно записать в виде последовательности следующих утверждений:
a ( A ∩ B) \ C a A ∩ B, a C a A, a B, a C a A \ C, a B \ C
a ( A \ C) ∩ (B \ C) .
По аналогии с объединением и пересечением двух множеств можно ввести
объединение и пересечение произвольного семейства множеств Ai , i I : |
||||||||
IAi |
={a |
|
|
|
a Ai |
для всех i I}, |
|
|
|
|
|
||||||
i I |
={a |
|
a Ai хотя бы для одного i I}. |
|
|
|||
UAi |
|
|
|
|||||
|
|
|
||||||
i I |
|
|
|
|
|
если I ={1, 2, ..., n}, то |
|
|
В частности, |
вместо IAi , |
UAi пишут |
||||||
|
|
|
|
|
|
|
i I |
i I |
|
|
|
n |
n |
|
|
||
соответственно IAi , |
UAi , или A1 ∩ A2 ∩... ∩ An , A1 A2 ... An . |
|||||||
|
i =1 |
i =1 |
|
|
||||
Если |
имеет место равенство A = UAi , |
то говорят, что |
множество А |
|||||
|
|
|
|
|
|
i I |
|
|
разложено в объединение своих подмножеств Ai , i I . Если при этом Ai ≠ при всех i I и Ai ∩ Aj = при i ≠ j , то говорят о разбиении множества А.
18

1.3 Отношения на множествах
Прежде чем определить строго понятие отношения, приведем примеры отношений из школьной математики. Такими примерами могут служить отношения «меньше», «больше» на числовых множествах, отношения параллельности и перпендикулярности на множестве прямых плоскости, отношение подобия многоугольников, отношение равносильности систем уравнений относительно одних и тех же неизвестных и т.д. В каждом случае отношение позволяет выделять из всех пар элементов множества такие пары (a, b) , в которых а связано этим отношением с b, например a < b, a ||b и т.п. В
связи с этим в общем случае принимается следующее определение: Отношением на множестве А называется любое подмножество декартова
квадрата A2 множества А.
Пусть ρ - любое отношение на множестве А. Тогда для любого элемента а из А можно определить подмножество [a]ρ ={b A: aρb}.
Так, если ρ есть отношение < на O O, то [a]ρ есть множество всех целых чисел, больших, чем а. Если ρ - отношение параллельности, то [a]ρ есть
множество всех прямых, параллельных прямой а, и т.д. Естественно возникает |
|
вопрос: для каких отношений |
ρ на А все различные подмножества типа [a]ρ |
образуют разбиение множества А? |
|
Отношение ρ на |
множестве A ≠ называется отношением |
эквивалентности, если оно обладает следующими свойствами:
1)ρ - рефлексивно, т.е. aρa для любого a A,
2)ρ - симметрично, т.е. aρb bρa для любых a, b A,
3)ρ - транзитивно, т.е. aρb, bρc aρc для любых a, b, c A.
В приведенных выше примерах отношениями эквивалентности являются отношения параллельности прямых, подобия многоугольников и равносильности систем уравнений.
Теорема Если ρ есть отношение эквивалентности на множестве А, то все попарно различные подмножества типа [a]ρ образуют разбиение
множества А.
Доказательство. Из определения соотношения эквивалентности видно, что a [a]ρ , и поэтому каждое из множеств [a]ρ не пусто и каждый элемент из А
содержится хотя бы в одном из таких подмножеств. Остается доказать, что любые |
|||
два подмножества [a]ρ , [b]ρ |
либо совпадают, |
либо |
не пересекаются. Пусть |
[a]ρ ∩[b]ρ ≠ , и x [a]ρ ∩[b]ρ . Тогда имеем соотношения: aρx и bρx . Из них, |
|||
используя свойства симметричности и транзитивности, |
получим xρa и bρa . Если |
||
с – любой элемент из [a]ρ , то имеем aρc , что вместе с bρa приводит к |
|||
соотношению bρc . Следовательно, c [b]ρ , |
т.е. |
[a]ρ [b]ρ . Аналогично |
|
доказывается и обратное включение. Таким образом, из наличия во множествах [a]ρ , [b]ρ одного общего элемента х следует их полное совпадение. Значит,
19
различные подмножества типа [a]ρ либо совпадают, либо не пересекаются.
Теорема доказана.
Если ρ есть отношение эквивалентности, то элементы, связанные отношением ρ , называются эквивалентными, а подмножества [a]ρ - классами
эквивалентности. Подчеркнем, что в этом случае все элементы одного класса эквивалентны между собой, а любые элементы из разных классов – не эквивалентны.
1.4 Отображения множеств
Большую роль в математике имеет установление связей между двумя множествами X и Y , связанное с рассмотрением пар объектов, образованных из элементов первого множества и соответствующих элементов второго множества. Особое значение при этом имеет отображение множеств.
Пусть X , Y - произвольные множества. Отображением множества X в множество Y называется всякое правило f, по которому каждому элементу
множества |
X сопоставляется вполне |
определенный (единственный) |
элемент |
множества Y . |
|
|
|
Тот |
факт, что f есть отображение X в Y , кратко записывают |
в виде: |
|
f : X →Y . |
|
|
|
Применяют также обозначение |
X R Y . Чаще отображения обозначают |
||
буквами f, q, F. |
f множества Х в множество |
Y , надо |
|
Итак, чтобы задать отображение |
|||
каждому элементу x X поставить в соответствие один и только один элемент y Y .
Если при этом элементу х из Х сопоставлен элемент y из Y, то y называют
образом элемента х, а х – прообразом элемента y при отображении f , что записывается в виде f (x) = y .
Из определения отображения f следует, что у каждого элемента x из Х образ единственный, однако для элемента y Y прообразов может быть много, а может и вообще не быть. Множество всех прообразов элемента y Y называется
его полным |
прообразом |
и |
обозначается |
через |
f −1( y) . Таким |
образом, |
||||||||||
f −1( y) ={x X |
|
f (x) = y}. |
|
|
|
|
|
|
|
|
|
|
из А и |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
Естественным путем определяются образ |
f ( A1) |
подмножества |
A1 |
|||||||||||||
прообраз f −1(B ) подмножества B |
|
из В при отображении |
f : |
|
|
|||||||||||
f (A )= |
1 |
|
{f (a)}, f |
|
1 |
|
{f −1(b)}. |
|
|
|
|
|
|
|||
|
|
U |
−1(B |
)= |
|
U |
|
|
|
|
|
|
||||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
a A1 |
|
|
b B1 |
|
|
|
|
|
|
||||||
НапримерU |
,U пусть |
A ={0, 1, 2, 3, 4, 5, 6} |
и |
f |
- |
отображение |
А |
в А, |
||||||||
сопоставляющее каждому элементу а из А остаток от деления а на число 4. Тогда имеем:
20

f (0) = 0, f (1) =1, |
f (2) = 2, |
f (3) = 3, |
f (4) = 0, |
f (5) =1, f (6) = 2 ; |
|
||||||||||
f −1(0) ={0, 4}, |
|
f −1(1) ={1, 5}, f −1(2) ={2, 6}, |
f −1(3) ={3}, |
f −1(5) = ; |
|||||||||||
f ({0, 4, 5})={0, 1}, |
f −1({0, 1})={0, 1, 4, 5}. |
|
|
|
|
|
|
||||||||
В зависимости от свойств, образов и прообразов различают |
|||||||||||||||
отображения сюръективные, инъективные и биективные. |
|
|
|
||||||||||||
Отображение |
f : X →Y называется сюръективным, если |
f (X ) =Y , т.е. |
|||||||||||||
каждый |
элемент из |
|
Y |
отображается |
хотя |
бы |
один элемент из |
Х, или |
|||||||
f −1( y) ≠ при любом |
y Y . |
|
|
|
|
|
|
|
|
||||||
Отображение |
|
|
f : X →Y |
называется |
инъективным, |
если |
разные |
||||||||
элементы множества Х отображаются в разные элементы множества |
Y т.е. |
||||||||||||||
f (x ) = f (x |
2 |
) x = x |
2 |
, |
|
или |
f −1( y) |
является |
либо |
пустым, |
либо |
||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
одноэлементным множеством при любом y Y . Инъективные отображения называются также вложениями.
Отображение f : X →Y называется биективным, или взаимно однозначным отображением X на Y , если оно сюръективно и инъективно,
т.е. если f −1( y) |
есть одноэлементное множество при любом y Y . В этом |
||
случае можно определить отображения ϕ : Y → X , |
положив для любого |
y Y : |
|
ϕ( y) = x f (x) = y . Оно называется обратным к f |
и обозначается в виде |
f −1 . |
|
Изобразим для наглядности виды отображений. |
|
||
X →Y |
X →Y |
X →Y |
|
|
|
|
|
|
|
Сюръективное |
Инъективное |
Биективное |
|||
|
|
|
Рисунок 12 |
|
|
Отображение множества А в себя называется преобразованием множества А. Биективное преобразование множества А называется
подстановкой множества А.
Примером подстановки множества целых чисел может служить отображение f : Z → Z , определенное равенством f (a) = a +1, a Z .
Заметим еще, что отображение f множества А в В называют также
функцией, заданной на множестве А со значениями в множестве В. При этом элемент f (a) называют значением функции f точке а. Само множество А
21

называют областью определения функции f , а множество f ( A) B - областью значений функции f .
Функцию f : A → B зачастую трактуют как переменную величину y ,
принимающую значения из В и так зависящую от переменной величины х, принимающей значения из А, что каждому значению а переменной величины х
соответствует вполне определенное значение f (a) |
величины y . При этом пишут |
|||
y = f (x) и вместо «функция f » говорят «функция |
f (x) ». |
|||
|
РассмотримU |
различные отображения и определим их виды.U |
||
|
|
|
|
|
1) Пусть Х – множество окружностей на плоскости. Сопоставляя каждой окружности ее центр, получим отображение Х на Y . Это отображение f не
является инъективным, поскольку одна и та же точка может быть центром бесконечного множества окружностей. Но оно сюръективно, так как любая точка
– центр некоторой окружности. Поэтому обратное соответствие f −1 всюду определено, сюръективно, но не функционально.
2) |
Соответствие |
f : x → x2 , x R |
является числовой функцией заданной |
|
на всем множестве R действительных чисел. Множеством значений этой |
||||
функции является совокупность R1 неотрицательных чисел. |
Так как R1 ≠ R , то |
|||
функция f |
не сюръективна. Она и не инъективна, так как (−x)2 = x2 . Поэтому |
|||
она не имеет обратной функции. |
|
|
||
3) |
Отображение |
f : x → x3 , x R |
сюръективно и |
инъективно: для |
любого y R есть одно и только одно число x R такое, что x3 = y . Этим числом
является 3 |
y . |
|
|
|
4) |
Отображение f :x → |
1 |
, x R |
( R - множество неотрицательных |
|
||||
|
|
1 + x2 |
1 |
1 |
|
|
|
|
чисел) множества R1 в себя всюду определено, инъективно, но не сюръективно.
Действительно, для дроби 1 +1x2 , выполнено 0 < 1 +1x2 ≤1.
Поэтому множеством значений этой функции является промежуток (0, 1] .
Обратная функция определена на этом промежутке и принимает неотрицательные значения.
5) |
|
|
|
Отображение |
f :Z → Z , |
определенное |
|
правилом |
|
2a, |
|
|
a ≥ 0, |
|
|
|
|
|
|
f (a) = |
a |
|
−1, a < 0, |
является |
инъективным |
отображением. Оно |
не |
является |
|
2 |
|
|
|
|
|
|
|||
биективным, |
поскольку f (Z ) = N0 ≠ Z . Однако, если таким |
же |
образом |
||||||
определить отображение Z в N0 , то получим биективное отображение.
В теории и на практике часто приходится осуществлять последовательно различные отображения множеств. В связи с этим дадим определение:
Композицией отображений ϕ и f , где f : A → B , ϕ : B →C называется отображение f oϕ : A →C , определенное условием:
22
