
Unlock-Линейная алгебра Сикорская 1
.pdf
Верны следующие утверждения:
1) Число, сопряженное сумме комплексных чисел равно сумме чисел, сопряженных со слагаемыми:
z + w = z + w.
Действительно. Пусть z = a + bi , w = c + di , и потому
z+ w = (a + bi) + (c + di) = (a + c) + (b + d )i = (a + c)− (b + d )i =
=(a − bi) + (c − di) = z + w.
2) Число, сопряженное произведению комплексных чисел, равно произведению чисел, сопряженных множителям
zw = z w .
|
|
|
|
|
|
|
|
Действительно, если z = a + bi , w = c + di , то |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
= (ac − bd )− (ad + bc)i . |
|
||||||||||||
|
|
|
|
|
|
|
|
|
z w |
(a + bi)(c + di) |
(ac − bd) + (ad + bc)i |
|
|||||||||||||||||||||||||||
C другой стороны, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (a − bi)(c − di)= (ac − bd )− (ad + bc)i . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
z |
w |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
Получили одинаковые результаты, что и доказывает верность второго |
|||||||||||||||||||||||||||||||
утверждения. |
обратному z , |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
3) |
|
|
|
|
Если z ≠ 0 , то число сопряженное числу, |
обратно |
|||||||||||||||||||||||||||||
числу, сопряженному с z : |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
, (т.е. |
|
=1: |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1: z |
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
z |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
Действительно. Из равенства z |
=1 следует, |
что |
|
|
1 |
|
|
|
=1. |
Но тогда |
|||||||||||||||||||||
|
|
|
|
z |
=1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
z |
|
|||||||
|
|
1 |
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Возведение в степень комплексного числа |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
Выпишем еще раз целые степени мнимой единицы: |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i3 = i2 i = (−1)i = −i , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i4 = i3 i = (−i)i = −i2 = −(−1) =1, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i5 = i4 i =1 i = i , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i6 = i5 i = i2 = −1, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i7 = i6 i = (−1)i = −i , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i8 = i7 i = −i i = −i2 =1 и т.д. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В общем виде полученный результат можно записать так: |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i4n =1; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i4n+1 = i ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i4n+2 = −1; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i4n+3 = −i (n = 0, 1, 2,...) . |
|
|
|
|
|
|
|
|
|
(2.13) |
|||||||||||||||||||||
33

При возведении комплексного числа a + bi во вторую и третью степень пользуются формулой для квадрата и куба суммы двух чисел, а при возведении в степень п (п – натуральное число, n ≥ 4 ) – формулой бинома Ньютона:
(a + bi)n = an + an−1bi + n(1n −21) an−2 (bi)2 + n(n −1)(n − 2) an−3 (bi)3 +... +
+ |
n(n − |
1)...(n − (k −1)) |
a |
n−k |
(bi) |
k |
+... + (bi) |
n |
. |
(2.14) |
||
1 |
2 |
3 ... k |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
Для нахождения коэффициентов формулы (2.14) удобно пользоваться |
||||||||||||
треугольником Паскаля (смотри практическое занятие). |
|
|||||||||||
В правой части этого равенства степени мнимой единицы заменяют по |
||||||||||||
формулам (2.13) и приводят подобные члены. |
|
|
|
|||||||||
НапримерU |
,U возведем |
комплексное число z = 2 − 3i в третью |
степень, |
|||||||||
используя формулу куба |
суммы |
(формулу |
|
бинома Ньютона при |
n = 3 ): |
|||||||
(a −b)3 = a3 + 3a2b +3ab2 + b3 |
и то, что i2 = −1, i3 = −i , имеем: |
|
||||||||||
(2 − 3i)3 = 23 + 3 22 (−3i) + 3 2 (−3i)2 + (−3i)3 =8 − 36i − 54 + 27i = |
|
|||||||||||
= −46 −9i . |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, (2 − 3i)3 |
= −46 − 9i . |
|
|
|
||||||||
Извлечение квадратного корня из комплексного числа
Квадратным корнем из комплексного числа называется такое комплексное число, квадрат которого равен данному.
Обозначим квадратный корень из комплексного числа x + yi через u + vi , тогда по определению x + yi = u + vi .
Возведем обе части полученного равенства в квадрат
(u + vi)2 = x + yi ,
u2 + 2uvi + (vi)2 = x + yi , u2 + 2uvi − v2 = x + yi ,
(u2 − v2 ) + (2uv)i = x + yi ,
поскольку два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части соответственно, имеем:
u2 |
− v2 = x , |
2uv = y . |
(2.15) |
|
Возведем каждое из этих равенств в квадрат и сложим полученное: |
|
|||
+ |
(u2 − v2 )2 = x2 |
|
||
(2uv)2 = y2 |
|
|||
|
|
|||
(u2 − v2 )2 + 4u2v2 = x2 + y2 , |
|
|||
u4 |
− 2u2v2 |
+ v4 |
+ 4u2v2 = x2 + y2 , |
|
u4 |
+ 2u2v2 |
+ v4 |
= x2 + y2 , |
|
(u2 + v2 )2 = x2 + y2 , |
|
|||
34
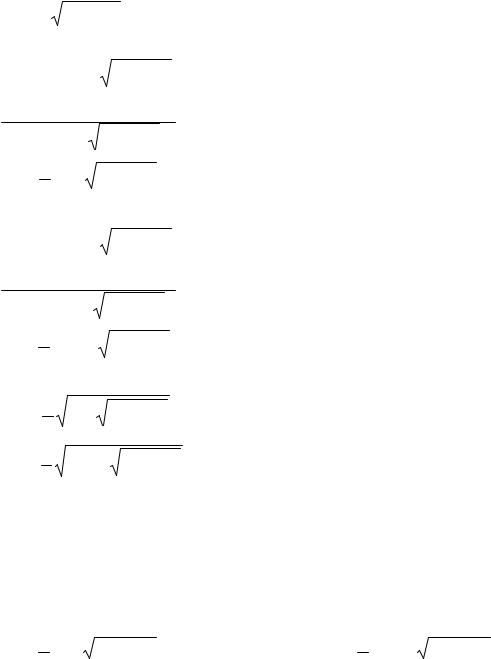
или u2 + v2 |
= |
|
x2 + y2 . |
|
|
(2.16) |
||||
Почленно сложив равенство (2.16) и первое из (2.15) находим u2 : |
||||||||||
|
2 |
+ v |
2 |
= |
x |
2 |
+ y |
2 |
, |
|
u |
|
|
|
|
||||||
+ |
2 |
|
|
2 |
|
|
|
|
|
|
|
− v |
= x, |
|
|
|
|
||||
u |
|
|
|
|
|
|
||||
2u2 = x + x2 + y2 , |
|
|||||||||
u2 = |
1 |
(x + x2 + y2 ). |
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
Теперь вычтем из (2.16) первое (2.15): |
||||||||||
|
2 |
+ v |
2 |
= |
x |
2 |
+ y |
2 |
, |
|
u |
|
|
|
|
||||||
− |
2 |
|
|
2 |
|
|
|
|
|
|
|
− v |
= x, |
|
|
|
|
||||
u |
|
|
|
|
|
|
||||
2v2 = −x + x2 + y2 , |
||
v2 = |
1 (− x + x2 + y2 ). |
|
|
2 |
|
Таким образом |
|
|
u = ± 1 |
x + x2 + y2 , |
|
|
2 |
|
v = ± |
1 |
− x + x2 + y2 . |
|
2 |
|
Знаки u и v выбирают так, чтобы полученные второму из равенств (2.15), то есть равенству 2uv = y .
(2.17)
u и v удовлетворяли
НапримерU |
,U извлечем квадратный корень из комплексного числа z = 5 +12i . |
|||||||||
Решение. |
Обозначим квадратный корень из числа |
z через u + vi , тогда |
||||||||
(u + vi)2 = 5 +12i . Поскольку в данном случае x = 5 , |
y =12 , то по формулам (2.17) |
|||||||||
получаем: |
1 (5 + |
52 +122 )= |
1 |
|
|
v2 = 1 |
(−5 + |
52 +122 )= 4; |
||
u2 = |
(5 +13) = 9 ; |
|
||||||||
|
|
|||||||||
|
2 |
|
|
2 |
|
|
2 |
|
|
|
u2 = |
9 ; u = 3 , u |
2 |
= −3; v2 = 4 , v = 2 , v |
2 |
= −2 . |
|
|
|||
|
1 |
|
1 |
|
|
|
||||
Таким образом, |
|
найдено два значения квадратного корня: u1 + v1i = 3 + 2i , |
||||||||
u2 + v2i = −3 − 2i . (Знаки выбрали согласно второму равенству из (2.15), 2uv = y , т.е. поскольку y =12 > 0 , то u и v одного комплексного числа одинаковых знаков.)
35
2.3 Тригонометрическая форма комплексных чисел. Операции над комплексными числами, заданными в тригонометрической форме
Геометрическое изображение комплексных чисел
Мы дали определение понятию комплексного числа и научились выполнять над комплексными числами арифметические действия, а также извлекать из них квадратные корни. Как уже отмечалось, одним из важнейших, является вопрос о практическом значении комплексных чисел. Чтобы ответить на этот вопрос, нужно сначала научиться изображать комплексные числа геометрически, подобно тому как изображаются действительные числа точками на координатной прямой.
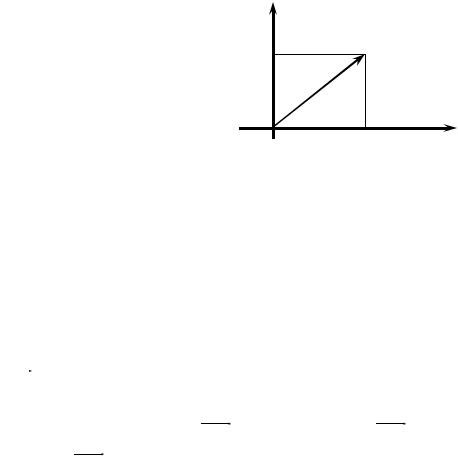
Комплексное число z = x + yi задается парой (x; y) действительных чисел. Рассмотрим эту пару чисел в качестве координат точки M (x; y) на координатной плоскости. Т.е. поставим в соответствие комплексному числу z = x + yi точку плоскости с координатами (x; y) и обозначим ее M (рисунок 13).
y
y |
M(x; y) |
0 |
x |
x |
Рисунок 13
Ясно, что при этом каждая точка координатной плоскости изображает одно и только одно число, а каждое число изображается одной и только одной точкой. Действительным числам соответствуют точки оси абсцисс, а чисто мнимым – точки оси ординат. Поскольку сопряженные числа отличаются только знаком мнимой части, то очевидно, что они изображаются точками координатной плоскости, симметричными относительно оси абсцисс.
Часто вместо точек на плоскости берут их радиус-векторы, т.е. векторы OM , началом которых служит точка O(0; 0) , концом M (x; y) . Ведь для того, чтобы найти координаты вектора надо от координат конца вычесть координаты начала. В нашем случае OM (x − 0; y − 0) , т.е. OM (x; y) , таким образом точка M
и вектор OM имеют одни и те же координаты.
Изображение комплексных чисел с помощью векторов удобно тем, что при этом получают простое геометрическое истолкование операций над ними. Мы знаем, что при сложении комплексных чисел отдельно складываются их действительные и мнимые части:
(a + bi) + (c + di) = (a + c) + (b + d)i .
36

Точно так же, при сложении векторов отдельно складываются их координаты: если OM (a; b) и ON(c; d) , то OM + ON = (a + b;c + d) . Это
означает, что при указанном соответствии операциям сложения и вычитания комплексных чисел соответствуют те же операции над векторами. Иными
словами, если числу z соответствует вектор OM , а числу w - вектор ON , то
числу z + w соответствует вектор OM + ON , а числу z − w - вектор OM −ON . Аналогично, при умножении комплексного числа z на действительное
число а соответствующий ему вектор OM умножается на это же число. Иными словами, числу az соответствует вектор a OM . В самом деле, на а умножаются как обе координаты вектора OM , так и действительная и мнимая часть числа z .
Полярная система координат и тригонометрическая форма комплексных чисел
Положение точки на плоскости можно задать различными способами. До этого момента мы работали с вами только с декартовой системой координат. Познакомимся с полярной системой.
Полярная система координат состоит из точки – полюса и полярной оси. При этом любая точка плоскости задается двумя координатами (r; ϕ),
называемыми полярными координатами: r - длина радиус-вектора точки.
ϕ - величина угла, образованного полярным лучом и радиус-вектором
точки.
Оговоримся заранее, что еще необходимо задать масштаб, ведь длину радиус-вектора надо измерить. Подробнее об этом вы узнаете в теме «Вектора».
В дальнейшем r будем называть модулем, а ϕ - аргументом.
Рисунок 14
Для того чтобы комплексное число z = x + yi записать в
тригонометрической форме совместим декартову и полярную системы координат следующим образом: начало координат совмещаем с полюсом, а ось абсцисс с полярной осью, тогда одна и та же точка М, изображающая комплексное число в
декартовой системе координат будет иметь координаты (x; y) , а в полярной
(r; ϕ).
37

|
|
|
|
|
|
Рисунок 15 |
|||
Достроив |
|
чертеж |
до прямоугольного |
треугольника OBM (гипотенуза |
|||||
OM = r , катеты BM = y , |
OB = x ) выразим x , y через r , ϕ . |
||||||||
x = r cosϕ, |
|
|
|
(2.18) |
|||||
y = r sinϕ. |
|
|
|
||||||
|
|
|
|
||||||
Таким образом, комплексное число z = x + yi запишем через r и ϕ : |
|||||||||
z = r cosϕ + ir sinϕ |
, |
|
|
|
|||||
z = r(cosϕ + isinϕ). |
|
||||||||
Из треугольника OBM выразим теперь r и ϕ через x и y . |
|||||||||
Имеем r 2 = x2 + y2 (теорема Пифагора) |
|
||||||||
r = x2 + y2 , |
|
|
|
|
|||||
(знак у корня +, так как r - длина, то есть величина неотрицательная). |
|||||||||
Далее, tgϕ = |
y |
(по определению тангенса острого угла прямоугольного |
|||||||
|
|||||||||
|
|
|
|
x |
|
y |
|
|
|
треугольника), следовательно ϕ = arctg |
. |
|
|||||||
|
|
||||||||
|
|
|
|
|
|
|
x |
z = x + yi однозначным образом |
|
Итак, всякое комплексное число |
|||||||||
записывается в виде |
|
|
|
|
|||||
z = r(cosϕ + i sinϕ), |
(2.19) |
||||||||
где r = x2 + y2 |
= z , |
|
|
|
|
||||
ϕ = arctg |
|
y |
= arg z . |
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
|||
Причем аргумент ϕ определен лишь с точностью до слагаемых, кратных |
|||||||||
2π . Назовем главным аргументом – наименьший положительный. |
|
|
|
|
|||||||
|
Запись комплексного числа (2.19) называется тригонометрической |
||||||||||
формой. |
|
|
|
|
|
|
π |
|
π |
|
|
|
НапримерU |
,U |
|
комплексные |
числа |
z |
|
+ isin |
|
||
|
|
= 2 cos |
2 |
2 |
, |
||||||
|
= cos13π + isin |
13 |
|
|
1 |
|
|
|
|||
z2 |
π заданы в тригонометрической форме, однако комплексные |
||||||||||
|
18 |
|
18 |
|
|
|
|
|
|
|
|
38
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
z5 = cos |
3 |
π + i sin |
7 |
|
|
||||
числа z3 = (−2) cos |
|
+ isin |
|
, |
|
z4 = 3 cos |
|
π − isin |
|
π , |
|
|
|
π |
||||||||||||||||||
5 |
5 |
|
3 |
3 |
4 |
4 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
даны не в тригонометрической форме, хотя их записи напоминают запись (2.19). |
|
|||||||||||||||||||||||||||||||
В тригонометрической форме эти числа запишутся так: |
7 |
|
|
|
7 |
|
|
|
|
|||||||||||||||||||||||
z |
|
|
6 |
|
+ isin |
6 |
|
|
, z |
|
|
4 |
π + isin |
4 |
|
|
z |
|
= cos |
π + isin |
π . |
|
|
|
||||||||
3 |
= 2 cos |
|
π |
|
π |
4 |
= 3 cos |
|
|
π , |
5 |
|
|
|
|
|
||||||||||||||||
5 |
5 |
3 |
3 |
4 |
4 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отметим Uособенности тригонометрической формы комплексного числа:U
1)первый множитель – неотрицательное число, r ≥ 0 ;
2)косинус и синус обязательно одного и того же аргумента;
3)мнимая единица умножена на синус угла.
Два комплексных числа, заданных в тригонометрической форме равны тогда и только тогда, когда их модули равны, а аргументы отличаются на величину, кратную 2π . Следовательно, если
r1 (cosϕ1 + isinϕ1 )= r2 (cosϕ2 + isinϕ2 ) , то r1 = r2 , ϕ2 =ϕ1 + 2πk ( k = 0, ±1, ± 2, ...).
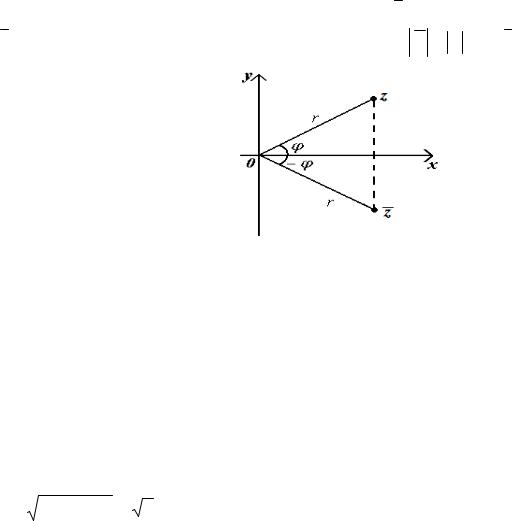
Если комплексное число z = x + yi задано в тригонометрической форме z = r(cosϕ + isinϕ), то сопряженное ему число z = x − yi записывается в форме z = r(cos(−ϕ) + isin(−ϕ)) (см. рисунок 16); поэтому z = z , arg z = −arg z .
|
Рисунок 16 |
|
|
|
НапримерU |
,U запишем комплексное число z = |
5 + i |
в алгебраической и |
|
2 + 3i |
||||
|
|
|
тригонометрической формах.
Решение. Сначала запишем заданное число в алгебраической форме:
5 + i |
= |
(5 + i)(2 − 3i) |
= |
10 −15i + 2i − 3i2 |
= |
10 −15i + 2i + 3 |
= |
13 −13i |
=1 |
− i . |
|||||||
2 + 3i |
(2 |
+ 3i)(2 − 3i) |
|
4 |
− 9i2 |
|
4 |
+ 9 |
|
|
13 |
||||||
|
|
|
|
|
|
|
|||||||||||
Чтобы записать комплексное число 1 − i в тригонометрической форме, воспользуемся формулами (2.19). Поскольку в данном случае x =1, y = −1, то
r = |
2 |
|
2 |
|
|
|
tgϕ = |
y |
|
−1 |
|
ϕ = − |
π |
+ 2πk , k Z . Таким |
||||
1 |
+ (−1) |
|
= |
2 , |
|
= |
1 |
, следовательно |
4 |
|||||||||
|
x |
|||||||||||||||||
образом, arg z = − |
π |
+ 2πk , k Z , а главный аргумент − |
π |
+ 2π = |
7π |
. |
||||||||||||
4 |
4 |
4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
39

Следовательно, комплексное |
число |
|
1 − i |
имеет следующую |
|||||
тригонометрическую форму: 1 − i = |
|
7π |
+ isin |
7π |
|
|
|||
2 cos |
4 |
. |
|
|
|||||
|
|
|
|
|
|
4 |
|
|
|
Действия |
над |
комплексными |
|
числами, |
заданными |
в |
|||
тригонометрической форме |
|
|
|
|
|
|
|
|
|
Рассмотрим два комплексных числа z1 и z2 , заданных в |
|||||||||
тригонометрической форме |
|
|
|
|
|
|
|
|
|
z1 = r(cos ϕ + i sin ϕ), |
z2 = ρ(cosψ + isinψ ) . |
|
(2.20) |
||||||
Произведение комплексных чисел |
|
|
|
|
|
|
|||
Выполняя умножение чисел (2.20), получаем |
|
|
|
||||||
z1 z2 = r(cosϕ + isinϕ)ρ(cosψ + isinψ )= |
|
|
|
|
|||||
= rρ(cosϕcosψ + i cosϕsinψ + isinϕcosψ − sinϕsinψ )= |
|
||||||||
= rρ((cosϕcosψ − sinϕsinψ )+ i(cosϕsinψ + sinϕcosψ )), |
|
||||||||
z1 z2 = rρ(cos(ϕ +ψ )+ i sin(ϕ +ψ )). |
|
|
|
|
(2.21) |
||||
Из равенства (2.21) следует, что |
|
|
|
|
|
|
|||
z1 z2 = z1 z2 , arg(z1 z2 ) = arg(z1) + arg(z2 ) ,
т.е. модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргументом произведения этих чисел является сумма аргументов сомножителей.
Сумму и разность комплексных чисел, заданных в тригонометрической форме, нельзя выразить формулами, подобными формуле умножения. Однако,
для модуля суммы имеют место следующие важные неравенства: |
|
z1 − z2 ≤ z1 + z2 ≤ z1 + z2 , |
(2.22) |
т.е. модуль суммы двух комплексных чисел меньше или равен сумме модулей слагаемых, но больше или равен разности этих модулей.
Неравенства (2.22) можно получить следующим путем. Пусть z1 = r1(cosϕ1 + isinϕ1) , z2 = r2 (cosϕ2 + isinϕ2 ) и пусть тригонометрическая форма
числа z1 + z2 есть z1 + z2 = R(cosψ + isinψ ) . Складывая отдельно действительные
и отдельно мнимые части, получаем: r1 cosϕ1 + r2 cosϕ2 = R cosψ , r1 sinϕ1 + r2 sinϕ2 = Rsinψ ;
умножая обе части первого равенства на cosψ , обе части второго – на sinψ и складывая полученное, имеем:
r1(cosϕ1 cosψ + sinϕ1 sinψ )+ r2 (cosϕ2 cosψ + sinϕ2 sinψ )= R(cos2ψ + sin2ψ ),
т.е.
r1 cos(ϕ1 −ψ )+ r2 cos(ϕ2 −ψ )= R .
40
Отсюда, так как косинус никогда не бывает больше единицы, следует
неравенство |
|
r1 + r2 ≥ R , т.е. |
|
z1 |
|
+ |
|
z2 |
|
≥ |
|
z1 + z2 |
|
. С другой стороны, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
z1 = (z1 + z2 ) − z2 = (z1 + z2 )+ (−z2 ) , но |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
z1 |
|
|
|
≤ |
|
|
|
z1 + z2 |
|
+ |
|
− z2 |
|
= |
|
z1 + z2 |
|
+ |
|
z2 |
|
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
откуда |
|
z1 |
|
− |
|
z2 |
|
≤ |
|
z1 + z2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Следует заметить, что для комплексных чисел понятия «больше» и «меньше» не могут быть разумно определены, так как эти числа, в отличие от действительных чисел, располагаются не на прямой линии, точки которой естественным образом упорядочены, а на плоскости. Поэтому сами комплексные числа (а не их модули) никогда нельзя соединять знаком неравенства.
Частное двух комплексных чисел
Пусть заданы комплексные числа (2.20) и пусть z2 ≠ 0 . Рассмотрим
частное |
z1 |
|
, имеем |
|
|
|
|
||||||
z2 |
= r(cosϕ + isinϕ)(cosψ − isin ρ) |
|
|||||||||||
|
|
|
|
|
|
|
|||||||
|
z1 |
= |
|
r(cosϕ + isinϕ) |
= |
||||||||
|
z2 |
|
|
|
|
|
ρ(cosψ + isinψ ) |
|
ρ(cosψ + isinψ )(cosψ − isinψ ) |
|
|
||
= |
|
r |
|
|
(cosϕcosψ + sinϕsinψ )+ i(sinϕcosψ + cosϕsinϕ) |
||||||||
|
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|
|
cos2 ψ + sin2 ψ |
||||||||
|
|
|
|
ρ |
|
|
|||||||
|
z1 |
= |
r |
(cos(ϕ − ψ)+ i sin(ϕ − ψ)). |
(2.23) |
|||||||||
|
z2 |
|
|
|||||||||||
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
||
Из этой тригонометрической формы частного следует, что |
||||||||||||||
|
z1 |
|
|
|
|
z |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
z1 |
|
|
|
||
|
|
|
|
= |
|
|
|
|
|
, arg |
|
|
= arg( z1 ) − arg( z2 |
) ; |
|
z2 |
|
|
|
z2 |
|
||||||||
|
|
|
|
|
z2 |
|
|
|
||||||
т.е. модуль частного комплексных чисел равен частному модулей числителя и знаменателя, а аргументом частного этих чисел является разность аргументов числителя и знаменателя.
Если |
|
|
z1 =1 =1(cos 0 + isin 0), z2 = ρ(cosψ + isinψ ) и |
ρ ≠ 0 , то формула |
|||||||||
(2.23) принимает вид |
|
||||||||||||
|
1 |
= |
|
|
1 |
|
(cos(0 −ψ )+ isin(0 −ψ )), |
|
|||||
|
ρ |
|
|||||||||||
|
z |
|
|
|
|
|
|
|
|||||
|
z−1 = |
|
1 |
|
|
= ρ−1(cos(− ψ)+ i sin(− ψ)), |
(2.24) |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
z |
|
|||||
откуда |
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
−1, arg z−1 = −arg z , |
|
|||||
|
z−1 |
|
|
= |
|
z |
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. модуль комплексного числа z−1 , обратного числу z , равен обратной величине модуля числа z , а его главное значение аргумента отличается от главного аргумента числа z только знаком.
41
Возведение в степень |
|
|
|
|
|
|
Переходим |
к вопросу |
о |
возведении в |
степень |
комплексного |
числа |
z = r(cosϕ + isinϕ) , |
заданного |
в |
тригонометрической |
форме. Если |
n - |
|
натуральное число, то с помощью формулы (2.21) |
получаем формулу |
|
||||
(r(cosϕ +i sinϕ))n = r n (cosnϕ + i sin nϕ) . |
|
|
(2.25) |
|||
Следовательно, при возведении комплексного числа в степень модуль возводится в ту же степень, а аргумент умножается на показатель степени.
Формула (2.25) будет верной и для целых отрицательных показателей.
Поскольку zn = (z−1 )n , то достаточно использовать эту формулу для числа z−1 , тригонометрическая форма которого определена формулой (2.24).
Формулу (2.25) называют формулой Муавра. Отметим частный случай этой формулы при r =1
(cosϕ + i sinϕ )n = cos nϕ + i sinnϕ. |
(2.26) |
Формула (2.26) имеет большое практическое приложение. Так частным случаем формулы Муавра (2.26) удобно пользоваться при выведении тригонометрических формул синуса и косинуса кратных углов.
НапримерU ,U выведем формулу синуса и косинуса двойного аргумента. Используя (2.26) при n = 2. Имеем
(cosϕ + isinϕ)2 = cos 2ϕ + isin 2ϕ ,
cos2 ϕ + 2isinϕcosϕ + i2 sin2 ϕ = cos2ϕ + isin 2ϕ, (cos2 ϕ −sin2 ϕ)+ (2sinϕcosϕ)i = cos2ϕ + isin 2ϕ .
Приравнивая действительные и мнимые части комплексных чисел, записанных справа и слева от знака равенства, имеем
cos2ϕ = cos2 ϕ −sin2 ϕ , sin 2ϕ = 2sinϕcosϕ .
Извлечение корня п-ой степени |
|
Пусть нужно извлечь корень п-ой степени из числа |
z = r(cosϕ + isinϕ) . |
Предположим, что это сделать можно и что в результате |
получается число |
ρ(cosψ + isinψ ) , т.е. |
|
[ρ(cosψ + isinψ )]n = r(cosϕ + isinϕ). |
(2.27) |
Применим формулу Муавра к левой части равенства (2.27), имеем
ρn (cos nψ + isin nψ ) = r(cosϕ + isinϕ)
Т.к. два комплексных числа равны только в случае, если их модули равны, то ρn = r ρ = n r .
А так как аргументы равных комплексных чисел отличаются на 2πk , k Z , то
42
