Unlock-Линейная алгебра Сикорская 1

2 Нахождение обратной матрицы с помощью элементарных преобразований

Для матриц больших размеров отыскание обратной матрицы удобно производить с помощью элементарных преобразований. Этот метод состоит в

следующем: выписывают составную матрицу (A E) и выполняют над строками

этой матрицы (т.е. одновременно и в матрице A, и в матрице E ) элементарные преобразования, приводящие матрицу A к виду единичной (более подробно о схеме преобразований сказано в практических разработках).

Врезультате матрица A преобразуется в единичную матрицу, а матрица E

-в матрицу A−1 .

Действительно, пусть одними и теми же элементарными преобразованиями над строками матриц A и E матрица A преобразована в единичную матрицу, а матрица E - в некоторую матрицу R . Это означает, что матрица R является результирующей матрицей преобразований, выполнение которых равносильно умножению слева на матрицу R . Поэтому имеем равенство

Запишем составную матрицу (A E) и преобразуем ее с помощью элементарных преобразований строк. В результате получим:

103

4.17 Простейшие матричные уравнения

К простейшим матричным уравнениям относят уравнения вида

AX = B , XC = B , AXC = B , AX = XB, AX + XB = C ,

в которых матрицы A, B, C заданы, а X - неизвестная матрица. Если матрицы A

и C имеют обратные матрицы, то первые три уравнения можно решить по соответствующим формулам:

X = A−1B , X = BC −1 , X = A−1BC −1 .

Для решения последних двух уравнений такой метод не подходит, так как решить подобные уравнения, опираясь только на формальное преобразование матричных выражений, нельзя. Во всех пяти случаях решение нельзя получить матричными преобразованиями и тогда, когда хотя бы один из сомножителей при

Тогда в подробной записи заданное матричное уравнение примет вид:

Вычислив произведения матриц в левой части уравнения и сложив эти произведения, приходим к уравнению

Записывая это матричное равенство поэлементно, получим следующую систему линейных уравнений:

104

решив которую находим

x1 = 2 , x2 = 3, y1 = 3, y2 = 4 . (решения системы линейных уравнений будем рассматривать в следующей главе)

Следовательно, искомая матрица имеет вид:

4.18 Ранг матрицы

Пусть дана прямоугольная матрица размеров m × n :

Рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля.

Если все миноры матрицы равны нулю, то ранг матрицы считается равным

нулю.

Ранг матрицы будем обозначать r (или rangA).

Непосредственно из определения ранга следуетU :U 1. Для матрицы размеров m × n

0 ≤ r ≤ min(m, n) ,

где min(m, n) - меньшее из чисел m и n .

2.r = 0 тогда и только тогда, когда все элементы матрицы равны нулю.

3.Для квадратной матрицы n -го порядка r = n тогда и только тогда, когда матрица невырожденная.

НапримерU ,U найдем ранг матрицы

Среди миноров первого порядка (элементов матрицы) есть отличный от нуля, значит, r > 0 . Все миноры второго и третьего порядков равны нулю, т.к. 1 и 3-й столбцы – линейно зависимы, а 2 и 4-й - нулевые. Следовательно, r =1.

Отметим свойство миноров матрицы, которым пользуются при нахождении ранга матрицы.

105

Если все миноры порядка k данной матрицы равны нулю, то все миноры более высокого порядка, если они существуют, также равны нулю.

Это следует, например, из теоремы о разложении определителя по элементам строки (столбца). Поэтому, если среди миноров порядка k данной матрицы есть отличные от нуля, а все миноры порядка k +1, если они существуют, равны нулю, то r = k . Отсюда следует, что ранг матрицы может быть найден следующим образом:

Если все миноры первого порядка (элементы матрицы) равны нулю, то r = 0 . Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то r =1. В случае, когда есть минор второго порядка, не равный нулю, исследуем миноры третьего порядка. Так поступаем до тех пор, пока не случится одно из двух: либо все миноры порядка k не

существуют либо все миноры порядка k равны нулю. Тогда r = k −1. Указанный метод нахождения ранга матрицы не всегда удобен, так как

часто связан с вычислением большого числа определителей. Ниже будут рассмотрены другие методы вычисления ранга матрицы.

Очевидны следующие свойства ранга матрицы.

1.Ранг матрицы, полученной из данной вычеркиванием какого-либо столбца (строки), равен рангу данной матрицы или меньше его на единицу.

2.Ранг матрицы, полученной из данной приписыванием к ней столбца (строки), элементами которого являются произвольные числа, равен рангу исходной матрицы или больше его на единицу.

3.Если вычеркнуть из матрицы или приписать к ней нулевой столбец (строку), т.е. столбец (строку), все элементы которого равны нулю, то ранг матрицы не изменится.

4.Ранг матрицы, полученной из данной транспонированием, равен рангу

данной матрицы.

Повторим уже известное нам: элементарными преобразованиями матрицы

называются следующие преобразования

1)умножение некоторого столбца (строки) матрицы на число, отличное

от нуля;

2)прибавление к одному столбцу (сроке) матрицы другого столбца (строки), умноженного на произвольное число;

3)перестановку местами двух столбцов (строк) матрицы

с учетом элементарных преобразований матрицы все свойства ранга матрицы можно выразить одной теоремой:

Теорема 4.5 (об инвариантности ранга матрицы относительно элементарных преобразований). Ранг матрицы, полученный из данной элементарными преобразованиями, равен рангу данной матрицы.

4.19 Методы вычисления ранга матрицы

1 Метод перебора

Это самый неэффективный метод. Суть его раскрыта в начале темы. Повторим коротко: считаются все миноры второго, третьего и т.д. порядка. Работа прекращается в том случае, когда обнаружилось, что все миноры, например, k -

106

того порядка равны нулю или не существуют, тогда делается вывод rang(A)= k −1.

2 Метод окаймляющих миноров

Метод окаймляющих миноров основывается на следующем рассуждении: если в матрице A имеется минор M порядка r , отличный от нуля, а все миноры матрицы A, окаймляющие минор M , равны нулю, или миноров, окаймляющих минор M , не существует, то ранг матрицы A равен r . Таким образом, для определения ранга матрицы достаточно найти отличный от нуля минор M , все окаймляющие миноры которого (если они существуют) равны нулю. Тогда ранг матрицы A равен порядку минора M .

Среди элементов матрицы A имеются отличные от нуля, например, элемент, стоящий в левом верхнем углу. Среди миноров, окаймляющих этот элемент, также есть отличные от нуля, например, минор

нет отличных от нуля. Следовательно, ранг матрицы A равен двум.

3 Приведение к треугольному (трапецевидному) виду

С помощью элементарных преобразований ненулевой матрицы A = (aij ) ее можно привести к матрице B следующего вида:

107

где bii ≠ 0 , i =1, ..., r , а элементы bij , расположенные в i -й строке (i =1, ..., r −1)

Приведение матрицы A к виду B состоит из r шагов.

Первый шаг.

а) Вычеркнем нулевые строки и столбцы матрицы A. Получившуюся матрицу снова обозначим буквой A, а ее элементы через aij .

б) Если a11 = 0 , то переставим строки и столбцы так, чтобы в левом

верхнем углу оказался элемент, отличный от нуля. Элементы получившейся матрицы A′ обозначим aij′ . При этом a11′ ≠ 0 . Если a11 ≠ 0 , то матрица A′ - это

Если при этом окажутся равными нулю также все элементы каждого столбца, начиная со второго, то, вычеркнув нулевые столбцы, придем к матрице B , у которой r =1. В противном случае сделаем второй шаг.

Второй шаг.

а) Вычеркнем нулевые строки и столбцы матрицы C . Получившуюся матрицу снова обозначим C , а ее элементы через cij .

б) Если c22 = 0 , то переставим строки и столбцы (причем первую строку и

108

d11 = c11′ ≠ 0 , d22 = c′22 ≠ 0 , а все элементы первой и второй строк, расположенные правее d11 и d22 , равны нулю:

Если окажутся равными нулю также все элементы каждого столбца, начиная с третьего, то, вычеркнув нулевые столбцы, придем к матрице B , у которой r = 2 . В противном случае сделаем третий шаг, полностью аналогичный первым двум шагам. Если ранг матрицы A равен r , то после r шагов получим матрицу B .

к треугольному виду, определим ее ранг.

третьей и четвертой строкам; поменяв местами вторую и четвертую строки во второй матрице, получили третью матрицу; четвертая матрица получена из третьей путем умножения второй строки на (−2) и прибавления к четвертой

строке, сложения второй и третьей строк.)

Так как ранг последней матрицы равен трем, для исходной матрицы также

r = 3 .

109

4.20 Базисный минор матрицы

Не равный нулю минор, порядок которого равен рангу матрицы, называется базисным минором данной матрицы. Столбцы и строки матрицы A, содержащие элементы базисного минора, называются базисными столбцами и

столбцы матрицы, во втором – первый и третий.

Теорема 4.6 (о базисном миноре) 1. Любая строка (столбец) матрицы является линейной комбинацией базисных строк (столбцов). 2. Базисные строки (столбцы) матрицы линейно независимы.

Доказательство. 1. Пусть M - базисный минор матрицы

Если хотя бы одно из чисел i или j не больше r , то ∆ij = 0 , так как в определителе имеются две одинаковых строки (столбца). При i > r , а также j > r

где α1, α2 , ..., αr , αr +1 - алгебраические дополнения элементов последней строки определителя ∆ij , причем очевидно, что числа α1, α2 , ..., αr не зависят от i , а

110

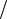где βi = −αi M .

Равенство (4.23) показывает, что j -й столбец матрицы A является

линейной комбинацией столбцов, проходящих через минор M , т.е. является линейной комбинацией базисных столбцов.

Аналогично доказывается, что всякая строка матрицы A является линейной комбинацией базисных строк.

2. Предположим, что базисные строки (столбцы) матрицы линейно зависимы. Тогда одна из базисных строк (столбцов) матрицы является линейной комбинацией остальных базисных строк (столбцов); следовательно, одна из строк (столбцов) базисного минора является линейной комбинацией остальных его строк (столбцов). Отсюда и из свойств определителей следует, что базисный минор равен нулю, что противоречит его определению. Теорема доказана.

Следствие 1 Всякая не базисная строка (столбец) матрицы является линейной комбинацией всех строк (столбцов) этой матрицы.

Следствие 2 Максимальное число линейно независимых строк (столбцов) матрицы равно рангу матрицы.

Следствие 3 (критерий равенства нулю определителя). Для того чтобы определить матрицы был равен нулю, необходимо и достаточно, чтобы некоторая его строка (столбец) была линейной комбинацией других ее строк (столбцов).

4.21 Вопросы для самоконтроля

1Сформулируйте определение матрицы и определите ее разновидность

взависимости от размеров (прямоугольная, квадратная, одностолбцовая, однострочная).

2Сформулируйте определения треугольной, диагональной, единичной

матриц.

3Сформулируйте определение субматрицы данной матрицы.

4Умножение матрицы на число (определение, свойства).

5Сумма матриц (определение, свойства).

6Что означает понятие линейной комбинации матриц?

7Что понимают под произведением строки A на столбец B одной и той же длины?

8При каком условии произведение прямоугольных матриц возможно?

9Сформулируйте правило умножения двух матриц.

10Сформулируйте и докажите основные свойства умножения матриц.

11Какое свойство называется основным свойством единичной матрицы?

12Докажите, что сумма и произведение диагональных матриц будет снова диагональной матрицей.

13Что означает степень матрицы и какими свойствами она обладает?

14Определите понятие многочлена от матрицы.

111

15Что означает действие транспонирования матрицы?

16Сформулируйте и докажите утверждение о транспонировании произведения двух матриц.

17Определите симметрическую и кососимметрическую матрицы.

18Сформулируйте и докажите утверждения о сумме симметрических и кососимметрических матриц.

19Сформулируйте определение обратной матрицы и её свойства.

20Сформулируйте определение ортогональной матрицы.

21Определите эрмитову, унитарную матрицы.

22Какой определитель называется квадратным?

23Какой определитель называется определителем третьей степени?

24Сформулируйте понятие определителя n -го порядка.

25Сформулируйте и докажите теорему Лапласа.

26Сформулируйте понятие минора элемента aij , алгебраического

дополнения элемента aij .

27Сформулируйте и докажите десять свойств определителя второго и третьего порядков.

28Сформулируйте свойства определителя n -го порядка.

29Перечислите методы вычисления определителей n -го порядка.

30Объясните суть метода вычисления определителя n -го порядка посредством его разложения по элементам строки (столбца).

31Объясните суть метода вычисления определителя n -го порядка приведением его к треугольному виду.

32Запишите формулу, на которой основан метод опорного элемента.

33Сформулируйте и докажите теорему об определителе произведения

матриц.

34Сформулируйте и докажите теорему о существовании обратной

матрицы.

35Какая матрица называется союзной?

36Перечислите известные вам методы нахождения обратных матриц.

37Запишите формулу нахождения обратной матрицы через алгебраические дополнения.

38Объясните суть метода нахождения обратной матрицы с помощью элементарных преобразований.

39Продемонстрируйте общий подход к решению матричного уравнения.

40Сформулируйте определение ранга матрицы.

41Перечислите известные вам методы нахождения ранга матрицы.

42Раскройте суть метода окаймляющих миноров.

43Опишите алгоритм метода нахождения ранга матрицы приведением ее

ктреугольному виду.

44Сформулируйте определение базисного минора матрицы.

45Сформулируйте и докажите теорему о базисном миноре.

112