6) степень согласованности целей при многостороннем выборе может варьироваться от полного совпадения интересов сторон (кооперативный выбор) до их противоположности (выбор в конфликтной ситуации). Возможны также промежуточные случаи, например, компромиссный выбор, коалиционный выбор, выбор в условиях нарастающего конфликта и т.д.

Различные сочетания перечисленных вариантов и приводят к многообразным задачам выбора, которые изучены не в одинаковой степени.

2.3. Критериальный язык описания выбора

Об одном и том же явлении можно говорить на языках различной общности. К настоящему времени сложилось три основных языка описания выбора.

Самым простым, наиболее развитым и, может быть, поэтому чаще употребляемым на практике является критериальный язык описания выбора. Это название связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критерия) и сравнение альтернатив сводится к сравнению соответствующих им чисел.

Пусть есть множество альтернатив Х. Пусть х – некоторая альтернатива из множества Х. Считается, что для всех х Х может быть задана функция (показатель, выражение) q (х), которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.д.) и обладает тем свойством, что если альтернатива х1 предпочтительнее альтернативы х2 (обозначается х1>х2), то q (х1)> q (х2), и обратно.

Если сделать предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий q (х) численно выражает оценку этих последствий, то наилучшей альтернативой х* является, естественно, та, которая обладает наибольшим значением критерия:

Задача отыскания х*, простая по постановке, часто оказывается сложной для решения, поскольку метод решения и сама возможность решения определяются как характером множества Х (размерностью вектора х и типом множества Х – является ли оно конечным, счетным или континуальным), так и характером критерия (является ли q (х) функцией или функционалом и какой или каким именно).

Однако сложность отыскания наилучшей альтернативы существенно возрастает, так как на практике оценивание любого варианта единственным числом обычно оказывается неприемлемым упрощением. Более полное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой. Например, при выборе конструкции самолета проектировщикам следует учитывать множество критериев: технических (высотность, скорость, маневренность, грузоподъемность, длительность полета и т.д.), технологических (связанных с будущим процессом серийного изготовления самолетов), экономических (определяющих затраты на производство, эксплуатацию и обслуживание машин, их конкурентоспособность), социальных (в частности, уровень шума, загрязнение атмосферы), эргономических (условия работы экипажа, уровень комфорта для пассажиров) и др.

Пусть для оценивания альтернатив используется несколько критериев qi (х), i= 1, …, p. Теоретически можно представить случай, когда во множестве альтернатив Х окажется одна альтернатива, обладающая наибольшими значениями всех р критериев. Она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор.

2.3.1. Сведение многокритериальной задачи к однокритериальной

Первый способ решения многокретериальных задач состоит в том, чтобы многокретериальную задачу свести к однокретериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:

20

Суперкритерий позволяет упорядочить альтернативы по величине q0, выделив тем самым наилучшую в смысле этого критерия. Вид функции q0 определяется тем, как представляется вклад каждого критерия в суперкритерий. Обычно используются аддитивные или мультипликативные функции:

i=1

Коэффициенты si обеспечивают:

1) безразмерность числа qi / si (частные критерии могут иметь разную размерность, и тогда

некоторые арифметические операции над ними, например сложение, не имеют смысла); 2) в необходимых случаях (как в формуле (2.4)) выполнение условия.

Коэффициенты αi и βi отражают относительный вклад частных критериев в суперкритерий. При данном способе задача сводится к максимизации суперкритерия:

q(х*) = max q0 (q1 (х), ..., qр (х))

хХ.

Очевидные достоинства объединения нескольких критериев в один суперкритерий сопровождаются рядом трудностей и недостатков, которые необходимо учитывать при использовании этого метода. Трудности могут быть связаны с построением самого суперкритерия или с методами вычисления. Но самое главное заключается в том, что даже небольшое изменение функции q0 может привести к тому, что оптимальная в новом смысле альтернатива окажется очень сильно отличающейся от старой.

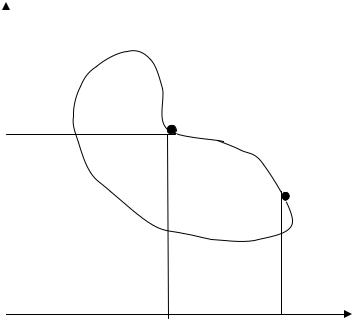
На рис. 2.1 видно, как изменяется выбор наилучшей альтернативы при простой смене коэффициентов в линейной упорядочивающей функции (формула 2.3), что отражается в наклоне соответствующей прямой:

q01 (х1*) > q01 (х2*), но q02 (х1*) < q02 (х2*).

q01 (х1)

q2

х1*

Х х2*

q02 (х)

q1

Рис. 2.1. Решение методом максимизации суперкритерия

Направления, соответствующие суперкритериям q01 и q02 изображены стрелками.

21

Идея такого упорядочения в многомерном пространстве заложена в некоторых балльных системах оценки вариантов.

2.3.2. Условная оптимизация

Недостатки свертывания нескольких критериев заставляют искать другие подходы к решению задач многокритериального выбора. Второй способ решения многокритериальных задач заключается в ином, нежели при свертывании, использовании того факта, что частные критерии обычно неравнозначны между собой. Одни из них более важны, чем другие. Наиболее явное выражение этой идеи состоит в выделении основного, главного критерия и рассмотрении остальных как дополнительных, сопутствующих. Такое различие критериев позволяет сформулировать задачу выбора как задачу нахождения условного экстремума основного критерия:

Решение задачи х* получается как максимизация критерия q1 на множестве Х при условии, что дополнительные критерии остаются на заданных им уровнях.

В некоторых задачах оказывается возможным или даже необходимым задавать ограничения на сопутствующие критерии не столь жестко, как в формуле 2.5. Например, если сопутствующий критерий характеризует стоимость затрат, то вместо фиксации затрат разумнее задавать их верхний уровень, т.е. формулировать задачу с ограничениями типа неравенств:

q2

С2

х1*

Х

х2х*2*

q1

Рис. 2.2. Решение методом условной оптимизации

На рис.2.2 приведены решения х1* задачи 2.5 и х2* задачи 2.6.

2.3.3. Поиск альтернативы с заданными свойствами

Третий способ многокритериального выбора относится к случаю, когда заранее могут быть указаны значения частных критериев или их границы, и задача состоит в том, чтобы найти альтернативу, удовлетворяющую этим требованиям, либо, установив, что такая альтернатива во множестве Х отсутствует, найти в Х альтернативу, которая подходит к поставленным целям ближе

22

всего. Характеристики решения такой задачи (сложность процесса вычислений, скорость сходимости, конечная точность и пр.) зависят от многих факторов.

Удобным свойством является возможность задавать желательные значения qi критериев как точно, так и в виде верхних или нижних границ; назначенные значения величин qi иногда называют уровнями притязаний, а точку их пересечения в р-мерном пространстве критериев – целью, или

опорной точкой, идеальной точкой.

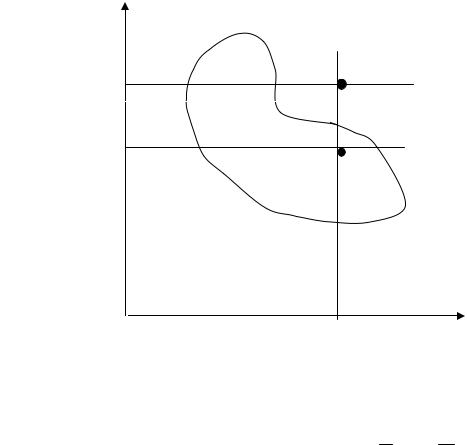
Поскольку уровни притязаний задаются без точного знания структуры множества Х в пространстве частных критериев, целевая точка может оказаться как внутри, так и вне Х (достижимая или недостижимая цель; на рис. 2.3 приведены оба варианта, соответственно, х1* и х2*).

q2

х1*

q1

Рис. 2.3. Поиск альтернативы с заданными свойствами

Теперь идея оптимизации состоит в том, чтобы, начав с любой альтернативы, приближаться к х* по некоторой траектории в пространстве Х. Это достигается введением числовой меры близости между очередной альтернативой х и целью х*, т.е. между векторами:

q(x) = (q1 (x), ..., q p (x)) и q(x) = (q1 (x), ..., q p (x)).

Можно по-разному количественно описать эту близость.

2.3.4. Нахождение паретовского множества

Четвертый полностью формализованный способ многокритериального выбора состоит в отказе от выделения единственной и наилучшей альтернативы и соглашении о том, что предпочтение одной альтернативе перед другой можно отдавать только, если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми. В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой (недоминируемые) принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето, и выбор на этом заканчивается. При необходимости же выбора единственной альтернативы следует привлекать дополнительные соображения: вводить новые добавочные критерии и ограничения либо бросать жребий, либо прибегать к услугам экспертов.

q2

23