3.2.2. Цилиндрическая оболочка

Рассмотренную выше задачу, изложенную в п. 3.1.3, представим в несколько иной постановке, а именно: выполним анализ силового нагружения корпуса ракеты, т.е. цилиндрической оболочки. При этом для иллюстрации возможностей различных методов задачу будем решать методом геометрического программирования.

ММ состоит, как обычно, из ЦФ, которой является вес оболочки (первое уравнение системы), и ограничений на прочность (остальные уравнения следующей системы):

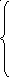
В соответствии с требованием алгоритма метода приведем задачу к стандартному виду:

,

или

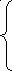
где ; ;

; .

Степень трудности данной задачи .

Следовательно, задача сводится к анализу системы нескольких линейных и одного нелинейного уравнения.

При этом матрица экспонент имеет вид

_.

Система линейных уравнений, включающая условия нормализации и ортогональности, преобразуется к виду

.

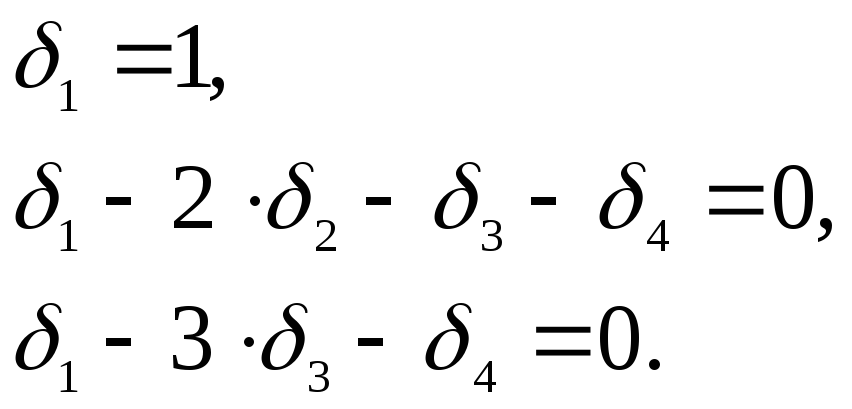
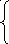Двойственная функция находится из выражения

.

На основе разработанной ММ можно записать:

, .

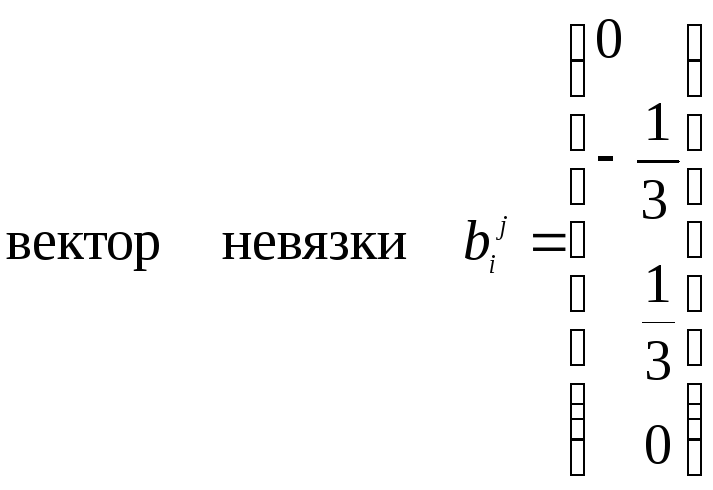Далее запишем уравнение равновесия

,

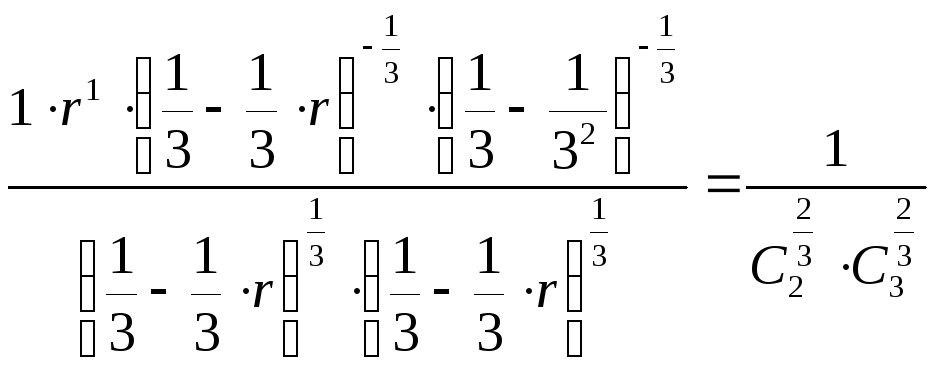
из которого можно определить базисную переменную r:

; ; .

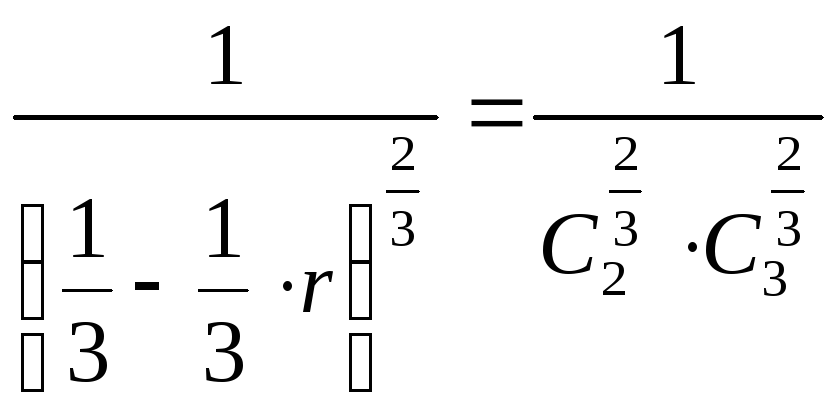В связи с этим можно записать: ,

,

.

Представленные формулы для двойственной функции и переменных позволяют рассчитать оптимизируемые параметры и вес цилиндрической оболочки по заданным исходным данным.

3.2.3. Бак с жидкостью

Данная задача, имеющая практическое значение при проектировании топливных баков ракет, формулируется следующим образом.

Минимизировать вес замкнутого тонкостенного бака высотой h, вмещающего, по крайней мере, объем V жидкости при давлении P, выбрав в качестве переменных проектирования средний радиус R и толщину стенок t. Требуется, чтобы напряжение в окружном направлении не превышало [σ_c], а окружная деформация была меньше [ε].

Указанные напряжения и деформации соответственно задаются выражениями σ_с=PR/t; ε=PR(2-μ)/(2Et),

где E=2·10¹¹-модуль Юнга; μ=0,3- коэффициент Пуассона.

Решение

Для решения задачи методом Куна-Таккера составляется функция Лагранжа, которая имеет вид:

L(x)=f(x)-Σν_ig_i(x),

где ЦФ является вес бака, определяемый по формуле:

f(x)=(π(R+t/2)²-π(R-t/2)²)hρg,

а ограничения на прочность, деформацию и объем находятся соответственно по формулам:

1) g₁(x)=PR/t-σ_c<0;

2) g₂(x)=PR(2-μ)/(2Et)-[ε] <0;

3) g₃(x)=-hπ(R-t/2)²)+V<0.

После нахождения производных функции L(x) по оптимизируемым параметрам исследуемая система уравнений дополняется следующими выражениями:

4) L/ R=2hρgt-ν₁P/t-ν₂P(2-μ)/(2Et)+ν₃(2πRh-πth)=0;

5) L/ t=2hρgR+ν₁PR/t²+ν₂PR(2-μ)/(2Et²)+ν₃(πth/2-πRh)=0.

Как уже было отмечено ранее (см. п. 3.1.3), необходимо рассмотреть следующие соотношения множителей Лагранжа и ограничений:

1) ν1>0,ν2>0, ν3>0; g1=0, g2=0, g3=0.

2) ν1=0,ν2>0, ν3>0; g2=0, g3=0.

3) ν1>0,ν2=0, ν3>0; g1=0, g3=0.

4) ν1>0,ν2>0, ν3=0; g1=0, g2=0.

5) ν1=0,ν2=0, ν3>0; g3=0.

6) ν1=0,ν2>0, ν3=0; g2=0.

7) ν1>0,ν2=0, ν3=0; g1=0.

8) ν1=0,ν2=0, ν3=0.

Исходные данные позволяют определить такой вариант сочетания ν иg, при котором параметры бака с жидкостью будут оптимальными.