Задача 2. Пусть нужно минимизировать позином

при

Соответствующая этой задаче двойственная задача состоит в максимизации двойственной функции:

при двойственных ограничениях:

δ₁≥0, δ₂≥0, δ₃≥0, δ₄≥0, δ₅≥0 - условие неотрицательности,

δ₁ + δ₂ + δ₃ = 1 - условие нормализации,

-δ₁ + δ₂ + δ₃ - 2δ₄ = 0,

-1/2δ₁ + δ₃ - 2δ₄ + 1/2δ₅ = 0, - условие ортогональности.

-δ₁ + δ₂ + δ₃ - δ₅ = 0.

Базисные векторы двойственного пространства получаются при использовании стандартной процедуры линейной алгебры, что является в данном случае методом Бранда. На первом шаге при помощи элементарных операций над столбцами матрицы экспонент она приводится к матрице «диагонального типа», например,

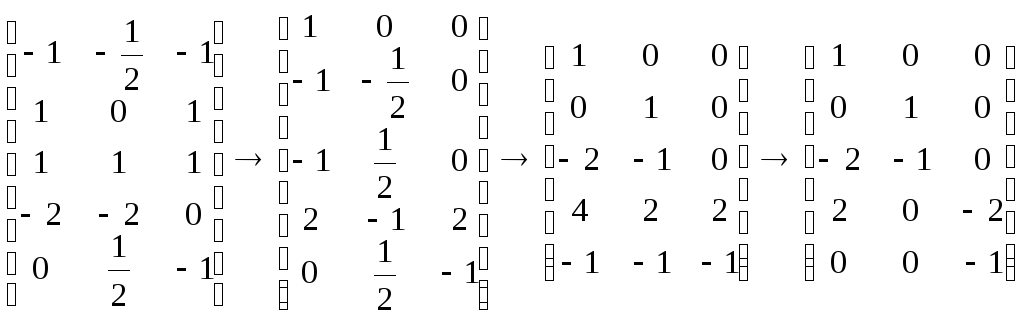(2.24)

Результирующая матрица «диагонального типа» может быть записана в более удобной форме:

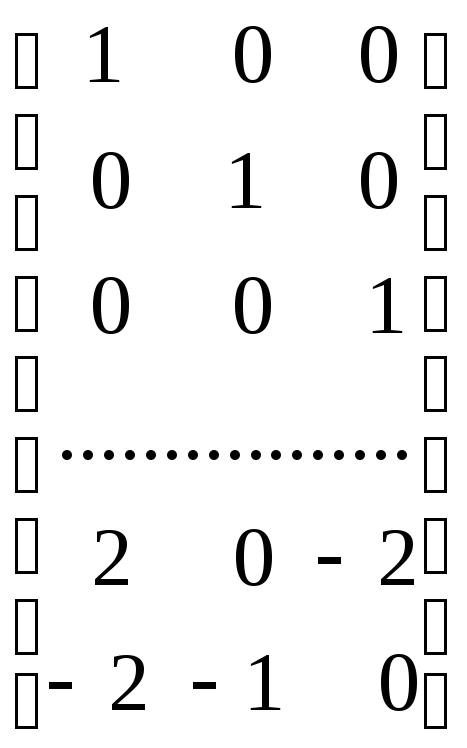(2.25)

в которой третью и пятую строки матрицы (2.24) необходимо было поменять местами, чтобы получить единичную (3 x 3) матрицу в верхней части преобразуемой матрицы. Далее, берут с обратным знаком матрицу, транспонированную к матрице, лежащей ниже единичной (3 x 3) матрицы, и дописывают к ней снизу единичную (2 x 2) матрицу, в результате получается:

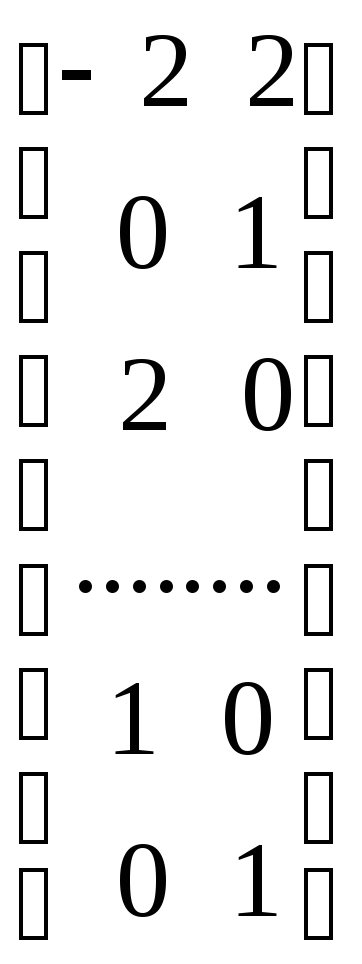. (2.26)

Из построения ясно, что любой вектор-столбец этой матрицы ортогонален ко всем векторам–столбцам матрицы (2.25). Однако нумерация компонент этих векторов–столбцов не соответствует нумерации в матрице (2.24), так как при переходе от (2.24) к (2.25) третья и пятая строки поменялись местами. Поэтому, меняя местами третью и пятую строки матриц (2.25) и (2.26), получают соответственно следующие матрицы:

(2.27) и 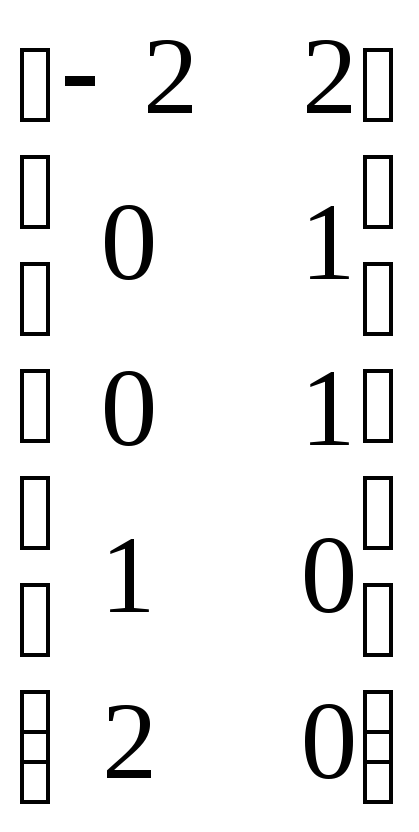. (2.28)

Векторы–столбцы матрицы (2.28) по построению ортогональны к векторамстолбцам матрицы (2.27). Так как матрицы (2.27) и (2.24) одинаковы, а (2.24) получена из матрицы экспонент при помощи элементарных операций над столбцами, можно заключить, что векторы–столбцы матрицы (2.28) ортогональны векторам–столбцам матрицы экспонент. Кроме того, векторы–столбцы матрицы (2.28) линейно независимы, они образуют базис пространства решений условий ортогональности, т. е. базис двойственного пространства.

Разделив первый вектор-столбец матрицы (2.28) на сумму первых трех его компонент, можно получить вектор

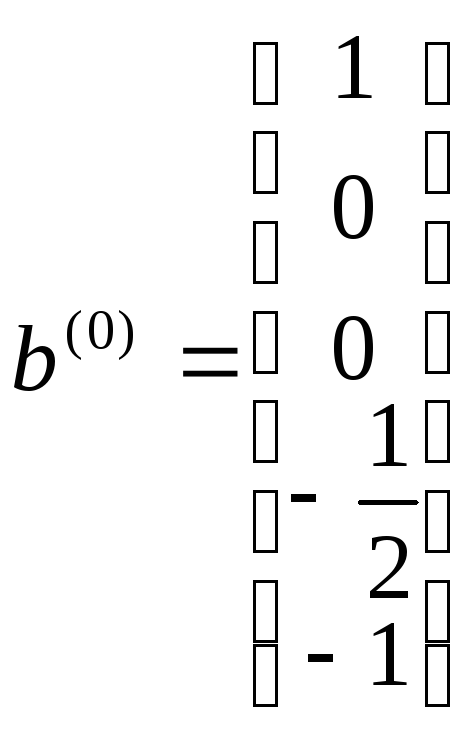(2.29)

который удовлетворяет как условию ортогональности, так и условию нормализации. Таким образом, b⁽⁰⁾ является вектором нормализации для задачи 2.

Так как матрица (2.28) имеет только два столбца, то для задачи существует лишь один вектор невязки b⁽¹⁾. Чтобы получить его, необходимо вычесть из оставшегося вектора–столбца матрицы (2.28) произведение суммы первых трех его компонент на вектор нормализации b⁽⁰⁾. В результате получается вектор

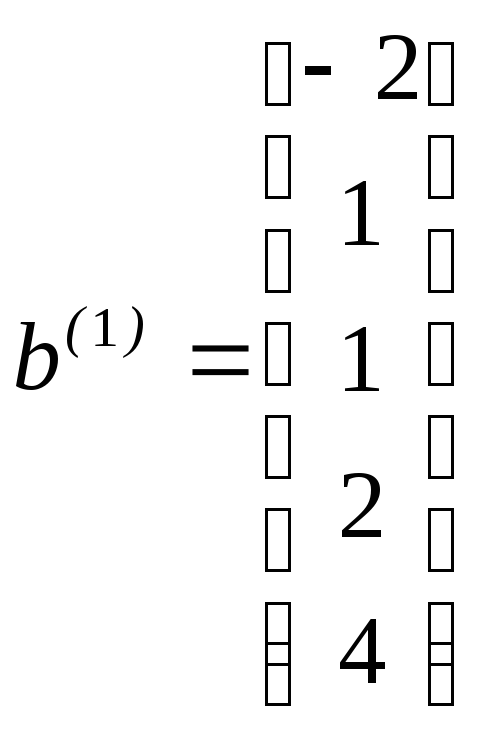(2.30)

Общее решение условий нормализации и ортогональности имеет вид

или

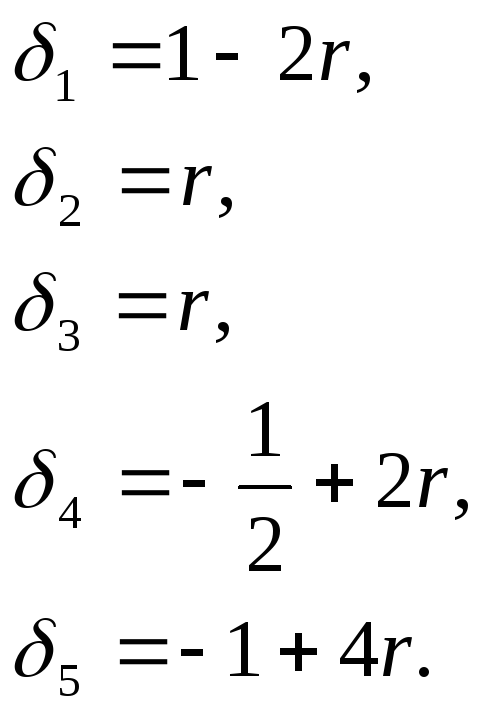(2.31)

Важно отметить, что вторым способом нахождения векторов нормализации и невязки является метод подстановки, заключающийся в обозначении одних двойственных переменных через базисные, число которых, как уже отмечалось, определяется степенью трудности решаемой задачи, и выражении других переменных из представленных выше условий. В данном случае при получается аналогичный результат.

Из полученных уравнений ясно, что δ удовлетворяет условиям неотрицательности только при таких значениях r:

. (2.32)

Подставляя в соотношения (2.30) значения r, равные, например, 1/4, 3/10 и 7/20, и вычисляя соответствующие значения двойственной функции, можно получить

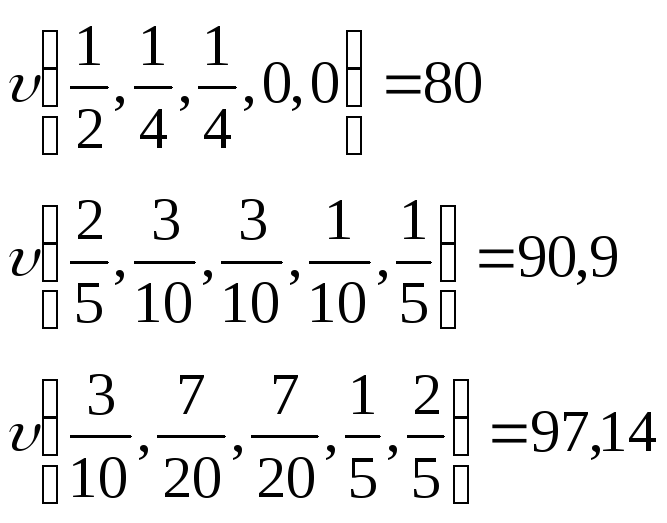(2.33)

Вычисляя f(x) для пробных значений x₁, x₂, x₃, которые удовлетворяют ограничениям прямой программы, получим

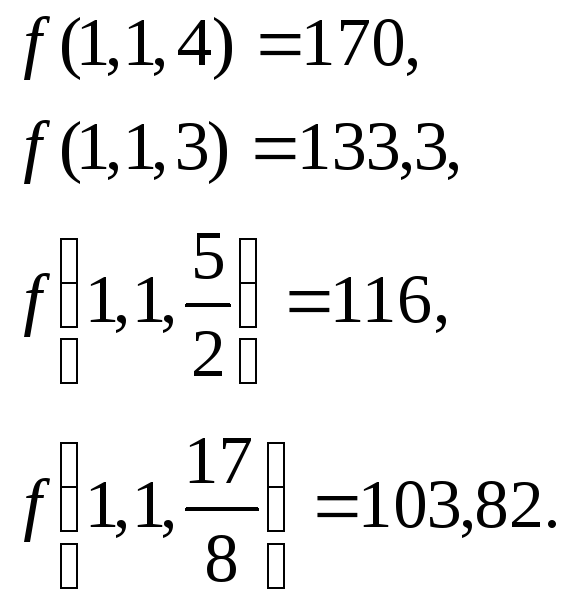(2.34)

Из соотношения двойственности можно записать

,

где x* - минимизирующий вектор задачи 2, a x и δ - произвольные векторы, удовлетворяющие соответственно ограничениям прямой задачи и двойственным ограничениям.

Следовательно, (2.33) дает оценки снизу для значения f(x*), тогда как (2.34) дает оценки сверху. В частности,

.

Следовательно, можно считать, что условный минимум ЦФ равен 100 с погрешностью, не превышающей 4 %.