
- •Министерство образования Российской Федерации
- •Введение
- •1. Принципы и структура сапр
- •1.1. Уровни проектирования
- •1.2. Классификация параметров объектов проектирования
- •1.3. Задачи проектирования
- •1.4. Стадии, аспекты и режимы проектирования
- •1.5. Компоненты сапр
- •1.6. Приципы построения комплексной сапр
- •2. Методы оптимизации
- •2.1. Постановка задачи оптимизации
- •2.2. Классификация критериев оптимальности и методов оптимизации
- •2.3. Классические методы исследования функций
- •2.4. Метод множителей лагранжа
- •Пример. Минимизировать
- •2.5. Метод куна – таккера
- •2.5.1. Условия Куна–Таккера
- •2.5.2. Необходимость условий Куна–Таккера
- •2.5.3. Достаточность условий Куна–Таккера
- •Требуется минимизировать
- •2.6. Оптимальное проектирование системы с распределенными параметрами
- •2.6.1. Вариационное исчисление
- •2.6.2. Частные случаи и примеры
- •2.7. Линейное программирование
- •2.7.1. Стандартная форма задач линейного программирования
- •2.6.2. Основы симплекс–метода
- •Из системы (2.20) при возрастании от 0 до 1 получаем новое решение:
- •Новое значение целевой функции находится по формуле
- •Относительная оценка небазисной переменной обозначается черези определяется по формуле
- •Пусть .
- •2.7.3. Целочисленное линейное программирование
- •2.8. Геометрическое программирование
- •2.8.1. Основные понятия и расчетные формулы
- •Где удовлетворяет указанным соотношениям.
- •Используя полученные выше неравенства и формулы, можно получить следующие соотношения между прямой и двойственной задачами.
- •2.8.2. Общий случай задачи гп
- •Двойственная функция этой задачи имеет вид
- •Задача 2. Пусть нужно минимизировать позином
- •2.8.3. Решение задач гп с ненулевой степенью трудности
- •3. Оптимальное проектирование
- •3.1.2. Цилиндрическая пружина кручения
- •3.1.3. Кольцевая колонна
- •3.1.4. Двутавровая балка
- •3.1.5. Колодочный тормоз
- •3.1.6. Подшипник скольжения
- •3.1.8. Анализ возможности применения метода геометрического программирования
- •3.1.8.1. Двухопорная цапфа
- •Вес маховика w и величина нагрузки на опоры с должны быть связаны неравенством
- •3.1.8.2. Стержневая конструкция
- •3.2. Расчет конструктивных элементов ракет
- •Решение
- •3.2.2. Цилиндрическая оболочка
- •3.2.3. Бак с жидкостью
- •Решение
- •3.3. Примеры апробированных задач проектирования
- •3.4. Газодинамические аспекты проектирования ракетных комплексов
- •3.5. Пример структурного синтеза зенитной пусковой установки
- •Заключение
- •Библиографический список
- •Содержание
Где удовлетворяет указанным соотношениям.
Рассмотрим следующую прямую задачу геометрического программирования.
Минимизировать
![]() при ограничениях
при ограничениях![]() .
.
Двойственная задача имеет следующий вид:
максимизировать
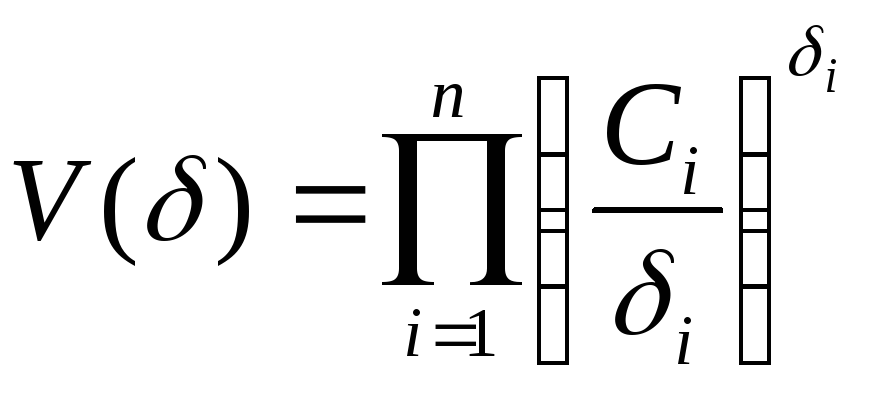 при ограничениях:
при ограничениях:
 ,
система неравенств называется условием
неотрицательности;
,
система неравенств называется условием
неотрицательности;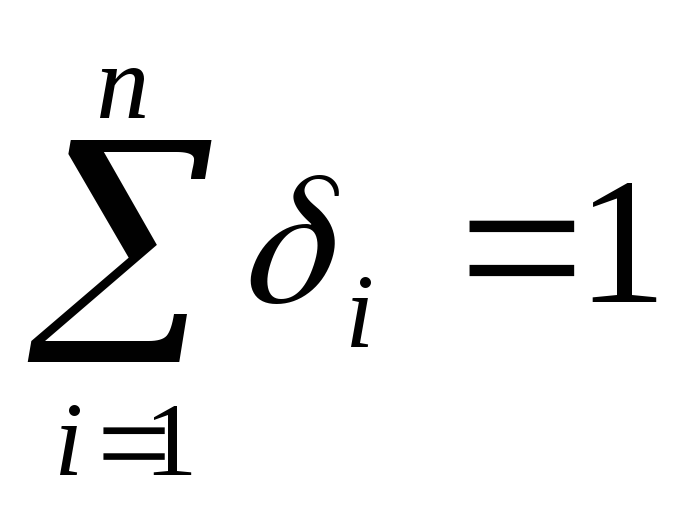 ,
данное уравнение называется условием
нормализации; следует учесть в дальнейшем,
что оно составляется только для
позиномов, входящих в ЦФ;
,
данное уравнение называется условием
нормализации; следует учесть в дальнейшем,
что оно составляется только для
позиномов, входящих в ЦФ;  ,
указанная система уравнений называется
условием ортогональности и составляется
для всех позиномов; причем коэффициенты
,
указанная система уравнений называется
условием ортогональности и составляется
для всех позиномов; причем коэффициенты
 - вещественные числа, элементы матрицы
экспонент ( или показателей) исходной
задачи.
- вещественные числа, элементы матрицы
экспонент ( или показателей) исходной
задачи.
Используя полученные выше неравенства и формулы, можно получить следующие соотношения между прямой и двойственной задачами.
Наличие оптимального решения в двойственной задаче представляет собой достаточное условие существования оптимума в прямой задаче.
Для соответствующих оптимумов
![]() .
.
Прямое и двойственное оптимальные решения связаны соотношением
![]()
или
![]() .
.
Допустимое решение двойственной задачи дает нижнюю границу оптимального значения ЦФ.
В случае ограничений, представленных позиномами, задача усложняется, однако подход остается аналогичным.
2.8.2. Общий случай задачи гп
Для вывода расчетной формулы воспользуемся основным тождеством
 .
.
Оно выполняется, так как по определению
![]() .
.
Следовательно,
 .
.
Рассмотрим
k–е ограничение, содержащее, например,
два позинома, записанных в общем виде:
![]() .
Из соотношения пропорциональности:
.
Из соотношения пропорциональности:![]() можно получить
можно получить![]() .
.
Введя
обозначения позиномов
![]() - для ЦФ и
- для ЦФ и![]() - для ограничений, а также учитывая, что
- для ограничений, а также учитывая, что![]() ,
из основного тождества получим
,
из основного тождества получим
 ,
,
где n – общее количество позиномов;
c – количество позиномов в целевой функции;
p – количество позиномов в k–м ограничении;
![]() - сумма двойственных переменных в k–м
ограничении, она составляется отдельно
для каждого ограничения.
- сумма двойственных переменных в k–м
ограничении, она составляется отдельно
для каждого ограничения.
Следовательно,
 .
.
Задача 1. Пусть требуется минимизировать позином
![]()
п![]() ри
ограничениях
ри
ограничениях
![]() .
.
Заметим, что в задаче четыре члена и только три переменных.
Двойственная функция этой задачи имеет вид
![]()
Условие нормализации представляется уравнением
![]()
а условия ортогональности – системой:

Эти
условия образуют систему, состоящую из
четырех линейных уравнений с четырьмя
неизвестными, и имеют единственное
решение (![]() ):
):
![]()
Значение двойственной функции в точке δ* таково:
![]()
Так
как δ* является единственной точкой
области определения υ(δ),
из теоремы двойственности мы заключаем,
что минимум функции
![]()
Следует
обратить внимание на то, что условный
минимум функции f(x) был определен до
нахождения минимизирующего вектора
(![]() ).
Исходя из смысла двойственной переменной
как весового коэффициента позинома,
можно записать для ЦФ
).
Исходя из смысла двойственной переменной
как весового коэффициента позинома,
можно записать для ЦФ![]() и
и![]() ,
,
для
ограничений
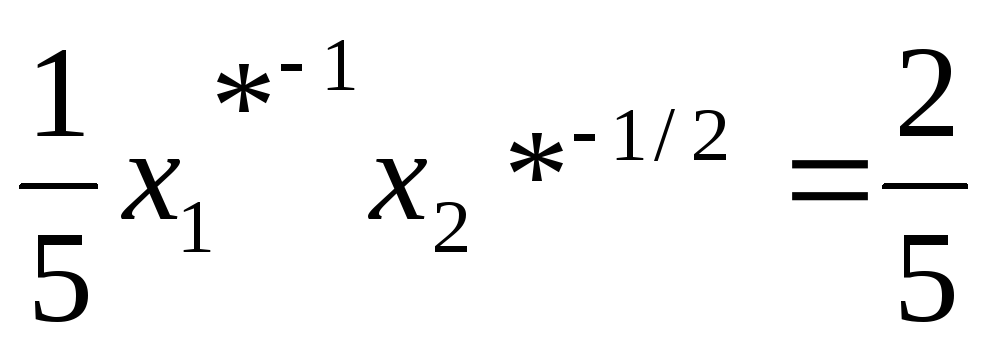 и
и .
.
Чтобы
определить значения
![]() ,
прологарифмируем обе части представленных
выше соотношений. Мы получим, что значения
,
прологарифмируем обе части представленных
выше соотношений. Мы получим, что значения
![]() удовлетворяют системе:
удовлетворяют системе:

которая линейна относительно переменных lnx1, lnx2 и lnx3. Она имеет единственное решение (-ln2, 0, 0), а это означает, что f(x) достигает условного минимума в точке (1/2, 1, 1).
Следовательно, поиск оптимизируемых параметров осуществляется путем решения системы уравнений, составленной из позиномов, число которых превышает количества неизвестных, однако любая комбинация уравнений дает одинаковый результат. Зачастую, для получения аналитических формул есть возможность преобразования расчетной системы уравнений без вычисления двойственной функции.
Если
степень трудности равна нулю, то
максимизирующий вектор δ*
не зависит от коэффициентов позинома.
Требование ортогональности, например,
трехкомпонентного вектора δ
двум векторам–столбцам матрицы
показателей полностью определяет вектор
на некотором двумерном подпространстве
трехмерного пространства. Поэтому
условие ортогональности может быть
сформулировано следующим образом:
вектор решения
![]() должен быть ортогонален пространству
показателей. Любой нормализованный
вектор, ортогональный пространству
показателей, называется двойственным
вектором. Для его построения используется
метод Бранда, который может быть
использован к любой матрице показателей.
должен быть ортогонален пространству
показателей. Любой нормализованный
вектор, ортогональный пространству
показателей, называется двойственным
вектором. Для его построения используется
метод Бранда, который может быть
использован к любой матрице показателей.
В соответствии с этим методом пространство, натянутое, например, на два вектора–столбца, остается неизменным при умножении любого из столбцов на постоянное число, а также при замене любого столбца на линейную комбинацию двух исходных столбцов. При использовании метода Бранда столбцы умножаются на константы, а затем берутся линейные комбинации таким образом, чтобы получилась единичная матрица в двух верхних строках матрицы показателей.
В предыдущей задаче размерность вектора показателей пбыла ровно на единицу больше размерности пространства показателейm, в результате чего условие ортогональности однозначно определяло двойственный вектор без проведения операции нормализации. Однако в общем случаеn > m +1, и поэтому условие ортогональности определяет лишь двойственное пространство. Размерность этого пространства равнаn - m. Очевидно, что произвольныйn-мерный векторvможет быть записан какv=e+δ,
где е—вектор показателей; δ - двойственный вектор.
С целью записи общего выражения для вектора δ, лежащего на гиперплоскости нормализации, вводится понятие вектора невязки. Вектор невязки δ(s) определяется как вектор, удовлетворяющий условию нормализации вида:
![]() .
.
Затем выбирается произвольный вектор δ, удовлетворяющий данному условию, например b(0). Тогда общее выражение для вектора δ, лежащего на гиперплоскости нормализации, будет иметь вид
![]() .
.
Здесь d на единицу меньше размерности двойственного подпространства, а именно d=n-(m+1). Ранее величина d была названа степенью трудности задачи. Коэффициенты rs, общее число которых равно d, называются базисными переменными.
-

Рис. 2.3. Графическая иллюстрация вектора нормализации и невязки
Понятия векторов нормализации и невязки могут быть проиллюстрированы в двумерном случае. На рис.2.3 гиперплоскость нормализации представляет собой прямую. Любой вектор, идущий от начала координат, с концом, лежащим на этой прямой, может быть выбран в качестве вектора нормализации. Любой вектор, лежащий на прямой нормализации, может быть выбран в качестве вектора невязки.
Для демонстрации использования векторов нормализации и невязки рассмотрим задачу минимизации, представленную выражением:
![]() ,
,
при
условии
![]() .
.
Ниже для рассматриваемой задачи приведена матрица для пространства показателей и ее двойственное пространство:


Последние два вектора двойственного пространства получены методом Бранда. Оба они удовлетворяют условию нормализации, поэтому любой из них может быть выбран в качестве вектора нормализации. Двойственный вектор невязки может быть получен просто как разность между этими двумя векторами, каждый из которых удовлетворяет представленному выше условию. Тогда формула

представляет собой наиболее общее выражение для двойственного вектора, удовлетворяющего условию нормализации.
